Расчет себестоимости передаваемой тепловой энергии

В качестве экономической задачи в данной работе нужно рассчитать плановую себестоимость передачи тепловой энергии тепловыми сетями с учетом прогнозирования возможных причин отказов, оказывающих большое влияние на величину планируемых расходов (затрат) на ремонт трубопроводов теплосетей и потерь тепловой энергии с утечками. Характерными причинами отказов являются: разрыв трубы, разрыв сварного шва, свищ, отказ арматуры, повреждение сальникового компенсатора.

В качестве метода прогнозирования, возможных причин отказов тепловых сетей в работе используется метод прогнозирования на основе выявления временного тренда, путем аналитического выравнивания уровней динамического ряда.

Глава 1. ПРОГНОЗИРОВАНИЕ ОТКАЗОВ ТЕПЛОВЫХ СЕТЕЙ

Методика статистического прогноза по тренду основана на предположении, что параметры тренда и колебаний сохраняются до прогнозируемого периода.

Данная методика расчета включает в себя несколько видов:

·  Выявление типа тренда;

·  Вывод уравнения тренда;

·  Анализ полученной зависимости;

·  Прогноз на требуемый период.

1.1 Выявление типа тренда

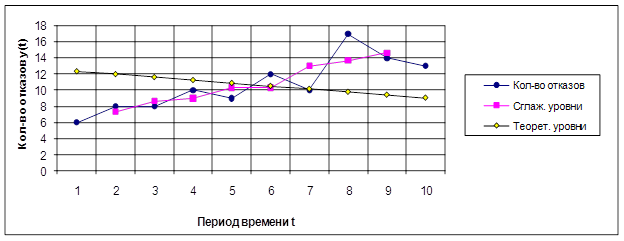
Для определения основной тенденции развития значения эмпирических уровней их изображают на графике y = f (t).

В качестве динамического ряда берется изменение количества отказов тепловых сетей за предлагаемый период времени в зависимости от характера отказа. Эмпирические уровни ряда сглаживаются методом скользящей средней. Сглаженные уровни наносят на график.

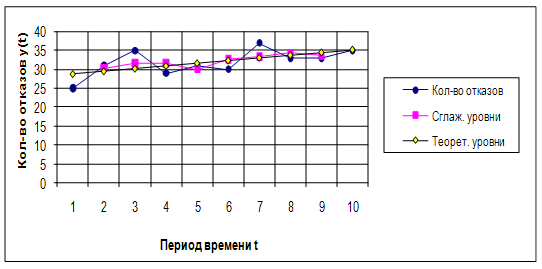Характер отказа – Свищ

Характер отказа – Разрыв трубы

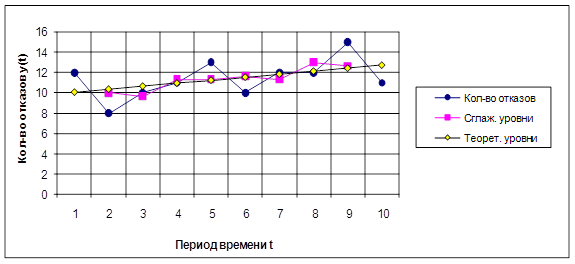
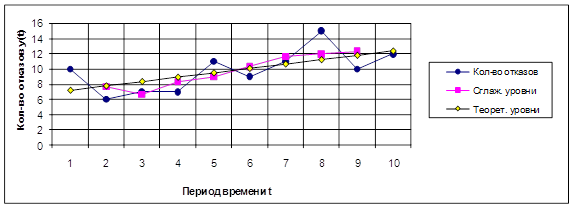
Характер отказа – Разрыв сварного шва

Характер отказа – Повреждение сальникового компенсатора

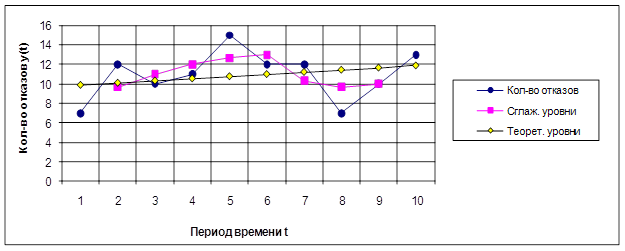
Характер отказа – отказ арматуры

1.2 ВЫВОД УРАВНЕНИЯ ТРЕНДА

На графическом изображении сглаженных уровней отчетливо проявляется основная тенденция изменения количества отказов тепловых сетей по различным причинам.

Следующим этапом работы является получение обобщенной статистической оценки тренда методом аналитического выравнивания.

Основная тенденция развития y_t как функция времени:

y_ti= f (t_i).

Определение теоретических (расчетных) уровней y_ti производится на основе адекватной математической модели, которая наиболее точно отображает основную тенденцию ряда динамики – количество отказов теплосети по данной причине.

Подбор математической функции основан на определении типа развития экономического явления во времени.

Когда тип тренда установлен, необходимо вычислить оптимальные значения параметров тренда, исходя из фактических уровней, т.е. получить значения коэффициентов уравнения. На основе требований метода наименьших квадратов (МНК) составляется система нормальных уравнений, решая которую, вычисляем параметры тренда.

Для линейного тренда нормальные уравнения МКТ имеют вид:

n*a + b*St _i= Sy _i

a*St _i + b*St²_i = S y_i *t_i

где y_i – уровни исходного ряда динамики;

t_i – номера периодов или моментов времени;

a, b – константы уравнений.

Нормальные уравнения МКТ для тренда в виде параболы 2-го порядка:

n*a + b*St_i + c*St_i² = Sy_i

a*St_i + b*St_i² + c*St_i³ = Sy_i*t_i

a*St_i² + b*St_i³ + c*St_i⁴ = Sy_i*t_i²

где y_i – уровни ряда динамики;

t_i – номера периодов или моментов времени;

a, b, c – константы уравнений.

Таблица 1.2.1 Формирование данных для вывода уравнения тренда – характер отказа свищ

свищ	Yi	скользящая средняя(3 г.)	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	25	-	1	25	1	25	1	1	1
1992	31	30,33333333	2	62	4	124	8	16	4
1993	35	31,66666667	3	105	9	315	27	81	9
1994	29	31,66666667	4	116	16	464	64	256	16
1995	31	30	5	155	25	775	125	625	25
1996	30	32,66666667	6	180	36	1080	216	1296	36
1997	37	33,33333333	7	259	49	1813	343	2401	49
1998	33	34,33333333	8	264	64	2112	512	4096	64
1999	33	33,66666667	9	297	81	2673	729	6561	81
2000	35	-	10	350	100	3500	1000	10000	100
итого	319	257,6666667	55	1813	385	12881	3025	25333	385

Для линейного тренда:

10*a +55*b = 319; a = 28;

55*a + 385*b = 1813; b = 0,71;

y = 28 + 0,71*t;

Для тренда в виде параболы второго порядка:

10*a + 55*b + 385*c = 319; a = 26,02;

55*a + 385*b + 3025*c = 1813; b = 1,7;

385*a + 3025*b + 25333*c = 12881; c = -0,09;

y = 26,02 + 1,7*t –0,09*t²;

Таблица 1.2.2 Формирование данных для вывода уравнения тренда – характер отказа разрыв трубы

разрыв трубы	Yi	скольз. ср. за 3 г.	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	12		1	12	1	12	1	1	1
1992	8	10	2	16	4	32	8	16	4
1993	10	9,666667	3	30	9	90	27	81	9
1994	11	11,33333	4	44	16	176	64	256	16
1995	13	11,33333	5	65	25	325	125	625	25
1996	10	11,66667	6	60	36	360	216	1296	36
1997	12	11,33333	7	84	49	588	343	2401	49
1998	12	13	8	96	64	768	512	4096	64
1999	15	12,66667	9	135	81	1215	729	6561	81
2000	11		10	110	100	1100	1000	10000	100
итого	114	91	55	652	385	4666	3025	25333	385

Для линейного тренда:

y = 9,75 + 0,3*t;

Для тренда в виде параболы второго порядка:

y = 9,82 + 0,26*t + 0,004*t²;

Таблица 1.2.3 Формирование данных для вывода уравнения тренда – характер отказа разрыв сварного шва.

разрыв св.шва	Yi	ср. скользящая за 3 г.	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	10		1	10	1	10	1	1	1
1992	6	7,666667	2	12	4	24	8	16	4
1993	7	6,666667	3	21	9	63	27	81	9
1994	7	8,333333	4	28	16	112	64	256	16
1995	11	9	5	55	25	275	125	625	25
1996	9	10,33333	6	54	36	324	216	1296	36
1997	11	11,66667	7	77	49	539	343	2401	49
1998	15	12	8	120	64	960	512	4096	64
1999	10	12,33333	9	90	81	810	729	6561	81
2000	12		10	120	100	1200	1000	10000	100
итого	98	78	55	587	385	4317	3025	25333	385

Для линейного тренда:

y = 6,61+ 0,58*t;

Для тренда в виде параболы второго порядка:

y = 7,27+ 0,25*t + 0,03*t²;

Таблица 1.2.4 Формирование данных для вывода уравнения тренда – характер отказа повреждение сальникового компенсатора

С/к	Yi	ср скользящая за 3 г.	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	7		1	7	1	7	1	1	1
1992	12	9,666667	2	24	4	48	8	16	4
1993	10	11	3	30	9	90	27	81	9
1994	11	12	4	44	16	176	64	256	16
1995	15	12,66667	5	75	25	375	125	625	25
1996	12	13	6	72	36	432	216	1296	36
1997	12	10,33333	7	84	49	588	343	2401	49
1998	7	9,666667	8	56	64	448	512	4096	64
1999	10	10	9	90	81	810	729	6561	81
2000	13		10	130	100	1300	1000	10000	100
итого	109	88,33333	55	612	385	4274	3025	25333	385

y = 9,69 + 0,22*t;

Для тренда в виде параболы второго порядка:

y = 7,66 + 1,36*t - 0,11*t²;

Таблица 1.2.5 Формирование данных для вывода уравнения тренда – характер отказа отказ арматуры

Отказ арматуры	Yi	ср. скользящая за 3 г.	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	6		1	0	0	0	0	0	1
1992	8	7,333333	2	8	1	8	1	1	4
1993	8	8,666667	3	16	4	32	8	16	9
1994	10	9	4	30	9	90	27	81	16
1995	9	10,33333	5	36	16	144	64	256	25
1996	12	10,33333	6	60	25	300	125	625	36
1997	10	13	7	60	36	360	216	1296	49
1998	17	13,66667	8	119	49	833	343	2401	64
1999	14	14,66667	9	112	64	896	512	4096	81
2000	13		10	117	81	1053	729	6561	100
	107	87	55	558	285	3716	2025	15333	385

Для линейного тренда:

y = 12,74 - 0,37*t;

Для тренда в виде параболы второго порядка:

y = 9,9 + 1,05*t - 0,129*t²;

1.3 Анализ полученной зависимости

Одним из применяемых на практике показателей адекватности математической функции для статистического изучения тренда является стандартизированная ошибка аппроксимации - s_yt:

где у_ti - теоретические уровни;

y_i - экспериментальные уровни;

n - число уровней ряда.

За наиболее адекватную принимается функция, у которой s_ytминимальная.

Правильность окончательных расчетов проверяется по равенству:

å y_i= å у_ti

Таблица 1.3.1 Расчет параметров тренда (характер отказа - свищ)

Yi	Ti	прям	параб	отклонения	прям	параб
				Yti-Yi	Yti-Yi 2	Yti-Yi	Yti-Yi 2
25	1	28,71	27,63	3,71	13,7641	2,63	6,9169
31	2	29,42	29,06	-1,58	2,4964	-1,94	3,7636
35	3	30,13	30,31	-4,87	23,7169	-4,69	21,9961
29	4	30,84	31,38	1,84	3,3856	2,38	5,6644
31	5	31,55	32,27	0,55	0,3025	1,27	1,6129
30	6	32,26	32,98	2,26	5,1076	2,98	8,8804
37	7	32,97	33,51	-4,03	16,2409	-3,49	12,1801
33	8	33,68	33,86	0,68	0,4624	0,86	0,7396
33	9	34,39	34,03	1,39	1,9321	1,03	1,0609
35	10	35,1	34,02	0,1	0,01	-0,98	0,9604
319	55	319,05	319,05	0,05	67,4185	0,05	63,7753

s_прямая = 2,5965; s_{парабола} = 2,5254;

Уравнение тренда имеет вид:

y = 26,02 +1,7*t-0,09 t²;

Таблица 1.3.2 Расчет параметров тренда (характер отказа – разрыв трубы)

Yi	Ti	прям	параб	отклонения	прям	параб
				Yti-Yi	Yti-Yi 2	Yti-Yi	Yti-Yi 2
12	1	10,05	10,08	-1,950	3,803	-1,916	3,671
8	2	10,35	10,36	2,350	5,523	2,356	5,551
10	3	10,65	10,64	0,650	0,423	0,636	0,404
11	4	10,95	10,92	-0,050	0,003	-0,076	0,006
13	5	11,25	11,22	-1,750	3,063	-1,780	3,168
10	6	11,55	11,52	1,550	2,403	1,524	2,323
12	7	11,85	11,84	-0,150	0,023	-0,164	0,027
12	8	12,15	12,16	0,150	0,023	0,156	0,024
15	9	12,45	12,48	-2,550	6,503	-2,516	6,330
11	10	12,75	12,82	1,750	3,063	1,820	3,312
114	55	114,00	114,04	0,000	24,825	0,04	24,817

s_прямая = 1,5756;

s_{парабола} = 1,5753;

Уравнение тренда имеет вид:

y = 9,82 + 0,26*t + 0,004*t²;

Таблица 1.3.3 Расчет параметров тренда (характер отказа – разрыв сварного шва)

Yi	Ti	прям	параб	отклонения	прям	параб
				Yti-Yi	Yti-Yi 2	Yti-Yi	Yti-Yi 2
10	1	7,19	7,550	-2,8100	7,8961	-2,4500	6,0025
6	2	7,77	7,890	1,7700	3,1329	1,8900	3,5721
7	3	8,35	8,290	1,3500	1,8225	1,2900	1,6641
7	4	8,93	8,750	1,9300	3,7249	1,7500	3,0625
11	5	9,51	9,270	-1,4900	2,2201	-1,7300	2,9929
9	6	10,09	9,850	1,0900	1,1881	0,8500	0,7225
11	7	10,67	10,490	-0,3300	0,1089	-0,5100	0,2601
15	8	11,25	11,190	-3,7500	14,0625	-3,8100	14,5161
10	9	11,83	11,950	1,8300	3,3489	1,9500	3,8025
12	10	12,41	12,770	0,4100	0,1681	0,7700	0,5929
98	55	98,00	98,00	0,0000	37,67	0,0000	37,188

s_прямая = 1,94087;

s_{парабола} = 1,92842;

Уравнение тренда имеет вид:

y = 7,27+ 0,25*t + 0,03*t²;

Таблица 1.3.4 Расчет параметров тренда (характер отказа – повреждение сальникового компенсатора)

Yi	Ti	прям	параб	отклонения	прям	параб
				Yti-Yi	Yti-Yi 2	Yti-Yi	Yti-Yi 2
7	1	9,910	8,910	2,9100	8,4681	1,9100	3,6481
12	2	10,130	9,940	-1,8700	3,4969	-2,0600	4,2436
10	3	10,350	10,750	0,3500	0,1225	0,7500	0,5625
11	4	10,570	11,340	-0,4300	0,1849	0,3400	0,1156
15	5	10,790	11,710	-4,2100	17,7241	-3,2900	10,8241
12	6	11,010	11,860	-0,9900	0,9801	-0,1400	0,0196
12	7	11,230	11,790	-0,7700	0,5929	-0,2100	0,0441
7	8	11,450	11,500	4,4500	19,8025	4,5000	20,2500
10	9	11,670	10,990	1,6700	2,7889	0,9900	0,9801
13	10	11,890	10,260	-1,1100	1,2321	-2,7400	7,5076
109	55	109,00	109,05	0,0000	55,3930	0,0500	48,1953

s_прямая = 2,3536;

s_{парабола} = 2,1953;

Уравнение тренда имеет вид:

y = 7,66 + 1,36*t - 0,11*t²;

Таблица 1.3.5 Расчет параметров тренда (характер отказа – отказ арматуры)

Yi	Ti	прям	параб	отклонения	прям	параб
				Yti-Yi	Yti-Yi 2	Yti-Yi	Yti-Yi 2
6	1	12,370	10,821	6,3700	40,5769	4,8210	23,2420
8	2	12,000	11,484	4,0000	16,0000	3,4840	12,1383
8	3	11,630	11,889	3,6300	13,1769	3,8890	15,1243
10	4	11,260	12,036	1,2600	1,5876	2,0360	4,1453
9	5	10,890	11,925	1,8900	3,5721	2,9250	8,5556
12	6	10,520	11,556	-1,4800	2,1904	-0,4440	0,1971
10	7	10,150	10,929	0,1500	0,0225	0,9290	0,8630
17	8	9,780	10,044	-7,2200	52,1284	-6,9560	48,3859
14	9	9,410	8,901	-4,5900	21,0681	-5,0990	25,9998
13	10	9,040	7,500	-3,9600	15,6816	-5,5000	30,2500
107		107,05	107,085	0,0500	166,0045	0,0850	168,9015

s_прямая = 4,0744;

s_{парабола} = 4,1097;

Уравнение тренда имеет вид:

y = 12,74 - 0,37*t;