Навигация
За май по средней гармонической взвешенной
2. за май по средней гармонической взвешенной
![]() x = Ex * f
x = Ex * f
Ex
x
![]() x = 1810.40+1533.30= 7397.57 руб.
x = 1810.40+1533.30= 7397.57 руб.
1810.40+1533.30
5.711+11.358
3. динамика среднемесячной заработанной платы
i = СМЗ май = 7397,57 = 0,986 (98,6%)
СМЗ апрель 7500,00
В мае СМЗ сократилась на 1,4%.
Задача 3. В целях изучения норм расходования сырья при изготовлении продукции на предприятии проведена 10%-я механическая выборка, в результате которой получено следующее распределение изделий по массе:
| Масса изделия, |
| До 20 | 20-21 |
| 22-23 |
| Итого |
| Число изделий, | шт. | 10 | 20 | 50 | 15 | 5 | 100 |
На основе этих данных вычислите:
1) среднюю массу изделия;
2) средний квадрат отклонений (дисперсию) и среднее
квадратичное отклонение;
3) коэффициент вариации;
4) с вероятностью 0,954-предельную ошибку выборочной
средней и возможные границы, в которых ожидается средняя
масса изделий;
5) с вероятностью 0,954-предельную ошибку выборочной
доли и границы удельного веса изделий массой от 20 до 23 кг.
Решение.
Чтобы определить среднюю величину из интервального ряда распределения, нужно его преобразовать в дискретный, например 20+21/2 = 20,5 кг.
Открытые интервалы нужно закрыть, приняв за величину интервала – значение интервала во второй группе.
Для удобства расчетов построим таблицу:
| Масса изделия, кг (x) | Число изделий, шт(ƒ) | Середина интервала, xi | Расчетные значения | |||
|
x.ƒ | x- | (x- | (x- | |||
| до 20 | 10 | 19,5 | 195 | -1,85 | 3,4225 | 34,22 |
| 20-21 | 20 | 20,5 | 410 | -0,85 | 0,7225 | 14,45 |
| 21-22 | 50 | 21,5 | 1075 | 0,15 | 0,0225 | 1,125 |
| 22-23 | 15 | 22,5 | 337,5 | 1,15 | 1,3225 | 19,83 |
| свыше 23 | 5 | 23,5 | 117,5 | 2,15 | 4,6225 | 23,11 |
| Итого | 100 | - | 2135 | - | - | 92,75 |
![]()
1) Средняя масса одного изделия
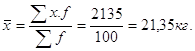
2) Дисперсия
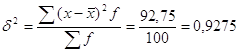
Среднее квадратическое отклонение
![]()
3) Коэффициент вариации
![]()
![]()
4) С вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидается средняя масса изделий
![]() ; t=2;
; t=2; ![]()
![]()
![]()
![]()
![]() , т.е.границы, в которых ожидается средняя масса изделий составляют
, т.е.границы, в которых ожидается средняя масса изделий составляют ![]() или 21,29-21,41кг.
или 21,29-21,41кг.
5) Предельная ошибка выборочной доли и границы удельного веса изделий массой от 20 до 23кг – с вероятностью 0,954.
![]() t=2
t=2 ![]()
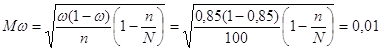
![]()
Удельный вес изделий массой от 20 до 23кг находится в пределах 85%±2%.
Задача 4. Среднемесячная заработная плата работающих в экономике Чувашской Республики характеризуется следующими данными:
| Год | 1998 | 1999 | 2000 | 2002 | |
| Среднемесячная заработная плата, р. | 600,2 | 847,7 | 1196,2 | 1726,4 | 2468,9 |
Для анализа динамики соответствующего показателя вычислить:
1) абсолютные приросты (снижение), темпы роста и прироста (снижения) по годам и по сравнению с 1998 г.; абсолютное содержание одного процента прироста (снижения). Результаты представить в виде таблицы;
2) среднегодовой уровень и среднегодовой абсолютный прирост (снижение);
3) среднегодовой темп роста и темп прироста.
Построить график. Сделать выводы.
Решение.
1) Анализ ряда динамики представим в таблице
| Год | СМЗ руб | Абсолютный прирост | Темп роста, % | Темп прироста, % | А% | |||
| цепн | баз | цепн | баз | цепн | баз | |||
| 1998 | 600,2 | - | - | - | - | - | - | - |
| 1999 | 847,7 | 247,5 | 247,5 | 141,24 | 141,24 | 41,24 | 41,24 | 6,002 |
| 2000 | 1196,2 | 348,5 | 596,0 | 141,11 | 199,3 | 41,11 | 99,3 | 8,477 |
| 2001 | 1726,4 | 530,2 | 1126,2 | 144,32 | 287,64 | 44,32 | 187,64 | 11,962 |
| 2002 | 2468,9 | 742,5 | 1868,7 | 143,01 | 411,35 | 43,01 | 311,35 | 17,264 |
| Итого | 6839,4 | 1868,7 | - | - | - | - | - | |
Способ расчета:
![]()
![]()
![]()
![]()
![]()
![]()
2) Среднегодовой уровень
![]() ;
; ![]()
Среднегодовой абсолютный прирост
![]()
3) Среднегодовой темп роста
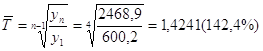
Среднегодовой темп прироста
![]()
Это значит, что в среднем за 4 года СМЗ увеличивалась на 42,4% в год.
График динамики СМЗ за 1998-2002 год.

Задача 5. Имеются данные о размере внешнего долга Российской Федерации (перед нерезидентами), млрд долл. США:
| 1.01.2003 | 1.04.2003 | 1.07.2003 | 1.10.2003 | 1.01.2004 | |
| Внешний долг | 153,2 | 155,4 | 160,1 | 166,7 | 184,2 |
Вычислите средний размер внешнего долга Российской Федерации за 2003 год. Поясните, почему методы расчета средних уровней рядов динамики в задачах 4 и 5 различны.
Решение.
Для расчета среднего уровня в моментных рядах динамики применяют несколько формул, в зависимости от характера самой зависимости. Если имеются данные на начало каждого периода и промежутки между ними равны, то расчет производят по формуле средней хронологической.
![]()
у = 0,5 у1 + у2 + у3 ………….+ 0,5у n
n -1
у = 0,5 *153.2 + 155.4 +160.1 +166.7 +.05*184.2 = 162.7 милр. руб.
4
А в задании 4 был дан интервальный (периодический) ряд динамики.
Задача 6. Динамика себестоимости и объем производства продукции характеризуется следующими данными:
| Вид продукции | Выработано продукции, тыс. шт. | Себестоимость единицы продукции, р. | ||
| Базисный год | Отчетный год | Базисный год | Отчетный год | |
| Предприятие №1 ST-280 AR-186 | 4,5 | 5,0 | 50,0 | 48,0 |
| 3,2 | 3,0 | 80,0 | 82,0 | |
| Предприятие №2 ST-280 | 10,6 | 10,0 | 70,0 | 76,0 |
На основании имеющихся данных вычислите: . 1) для предприятия №1 (по двум видам продукции вместе):
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Определите в отчетном периоде изменение суммы затрат на производство продукции и разложите по факторам (за счет изменения себестоимости и объема выработанной продукции). Покажите взаимосвязь между исчисленными индексами;
2) для двух предприятий вместе (по продукции ST-280):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства проекции на динамику средней себестоимости. -
Объясните разницу между величинами индексов постоянного и переменного состава.
Решение.
I. Для предприятия №1 (по двум видам продукции вместе)
а) Общий индекс затрат на производство продукции
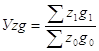 ;
; ![]()
![]()
б) общий индекс себестоимости продукции
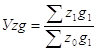 ;
; ![]()
![]()
в) общий индекс физического объема производства продукции
 ;
; ![]()
![]()
Взаимосвязь индексов: ![]() ; 1,018.0,99=1,0104
; 1,018.0,99=1,0104
По факторам: затраты увеличились на 5 тыс. руб. в отчетном периоде, это произошло за счет снижения себестоимости на 4 тыс. руб., а увеличение объема производства увеличило затраты на 9 тыс. руб. (9-4=5 тыс. руб.)
II. Для двух предприятий вместе (по продукции ST-280)
а) индекс себестоимости переменного состава
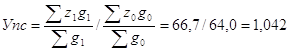
б) индекс себестоимости постоянного состава
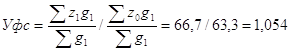
в) индекс структурных сдвигов
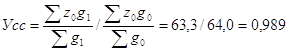
Взаимосвязь индексов: ![]() ; 0,989.1,054=1,042
; 0,989.1,054=1,042
Индекс переменного состава - результативный индекс, а два остальные – факторы, влияющие на среднюю динамику себестоимости.
Задача 7. Имеются следующие данные о товарообороте продовольственного магазина:
| Товарная группа | Продано товаров в фактических ценах, тыс. р. | Изменение цен, % | |
| III квартал | IV квартал | ||
| Мясо и мясопродукты | 612 | 594 | +5 |
| Молочные продукты | 368 | 402 | +3 |
Решение.
1. общий индекс товарооборота в фактических ценах
Урg = Ep1 * g1 = 594+402 = 1.016 (101.6%)
Ep0 * p0 612+368
Общий товарооборот в фактических ценах увеличился на 1,6%
2. общий индекс цен.
Ур = Ep1 * g1 = Ep1 * g1 = 594+402 = 996 = 1.042 (104.2%)
![]() Ep0 * p0 Ep1*g1 594+ 402 956
Ep0 * p0 Ep1*g1 594+ 402 956
Ip 1,05+1,03
Цены увеличились на 4,2 %
3. общий индекс физического объема товарооборота, используя взаимосвязь индексов.
Уg = Уgp; Уg = 1,016 = 0,975 ( 97,5)
Уp 1,042
Продано товаров в отчетном периоде меньше, чем в базисном, а товарооборот увеличился за счет увеличения цен на 4,2%.
Задача 8. Для изучения тесноты связи между объемом выпуска продукции на одно предприятие (результативный признак — у) и оснащенностью предприятия основными производственными фондами (факторный признак - х) по данным задачи 1 вычислите коэффициент детерминации и эмпирическое корреляционное отношение. Поясните их значения.
Решение.
1. Коэффициент детерминации (П2) = межгрупповая дисперсия / общая дисперсия.
![]()
![]() Межгрупповая дисперсия = E (xi – x0)2 * f,
Межгрупповая дисперсия = E (xi – x0)2 * f,
Ef
![]() Где хi- средняя ВП по каждой группе по задаче 1
Где хi- средняя ВП по каждой группе по задаче 1
![]() х0 – общая средняя по 25 предприятиям
х0 – общая средняя по 25 предприятиям
f – количество предприятий в каждой группе.
![]()
Дисперсия общая = Ex2 - (x)2
n
Таблица расчета межгрупповой дисперсии.
| N группы | Число предприятий |
хi | Расчетные показатели | ||
|
|
|
| |||
| I | 3 | 2,9 | -2,85 | 8,16 | 24,47 |
| II | 8 | 4,4 | -1,35 | 1,84 | 14,71 |
| III | 5 | 5,7 | -0,05 | 0,003 | 0,01 |
| IV | 7 | 7,1 | 1,34 | 1,80 | 12,64 |
| V | 2 | 10,5 | 4,74 | 22,50 | 45,01 |
| Итого | 25 | 5,7 | - | - | 96,85 |
σ2 межгр.= 96,85 = 3,874
25
Общая дисперсия = 934,07 - 33,13 = 4,231
25
П2 = 3,874 = 0,916 (91,6%)
4,231
Значит вариация ВП на 91,6% зависит от вариации ОПФ.
Похожие работы
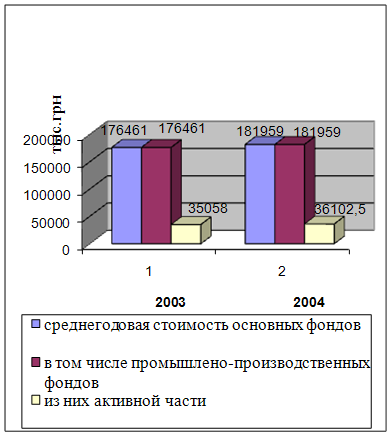
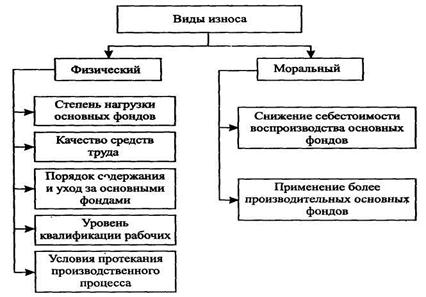
... лишь среднюю степень их износа. Разные группы основных средств могут быть изношены неодинаково, поэтому приведем таблицу об износе основных производственных фондов. Износ основных производственных средств по группам за 98 год представлен в таблице 4.2. Таблица 4.2. Процент износа основных производственных средств по группам. наименование Первоначальная стоимость Остаточная ...
... продукции и другие показатели; изучить степень использования производственной мощности оборудования; выявить резервы повышения эффективности использования основных производственных фондов. [6] Для оценки обеспеченности предприятия основными производственными фондами, анализа их состава и структуры используются данные основных средств, группового учета основных средств и плана экономического и ...
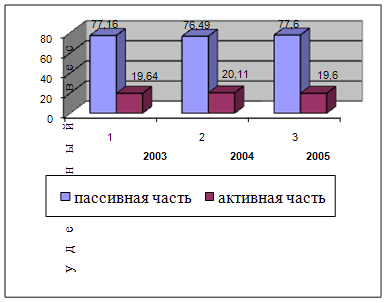
... оборудования (30,8%) имеет срок службы свыше 20 лет. Водоводы со сроком службы более 20 лет составляет 26,5% , коллектора – 33,3%. 2.3 Показатели оценки эффективности использования основных производственных фондов Важное значение имеет анализ изучения движения и технического состояния ОПФ, для этого рассчитаем следующие показатели, используя формулы (1.7), (1.8), (1.9), (1.10), (1.11), ...
... и оборотными производственными фондами зависит от особенностей отрасли. В материалоёмких отраслях, потребляющих дорогое сырьё и имеющих сравнительно простое оборудование доля основных производственных фондов относительно невелика, и, наоборот, в отраслях, применяющих сложное технологическое оборудование и использующих сравнительно недорогое сырьё доля основных производственных фондов значительно ...


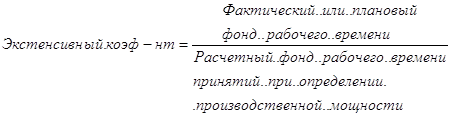
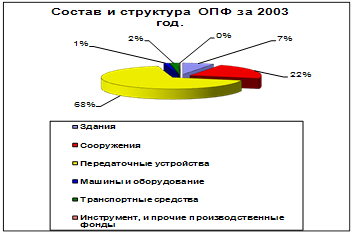
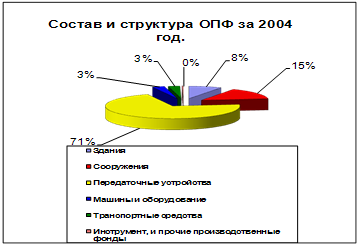
0 комментариев