Навигация
Ошибка репрезентативности возникает в силу того, что выборочная совокупность не полностью воспроизводит генеральную
12359
знаков
12
таблиц
0
изображений
1. Ошибка репрезентативности возникает в силу того, что выборочная совокупность не полностью воспроизводит генеральную.
Предельная ошибка выборки репрезентативности: 
(грн.), где
t- коэффициент доверия, вычисляемый по таблицам в зависимости от вероятности, при 0,9997 t=3.
μ- средняя ошибка выборки (грн.)
, (грн.), где
N- объем генеральной совокупности N=50000.
n – объем выборочной совокупности n=5000.
- дисперсия выборочной совокупности.
=0,24 грн.- средняя ошибка выборки
=3*0,24=0,72 грн.
предельная ошибка репрезентативности с вероятностью 0,997.
Зная среднюю величину признака (средний размер вклада = 300 грн.) и среднюю ошибку выборки, определим границы в которых заключена генеральная средняя:
(грн.)
300-0,24
300+0,24;
299,76300,24 (грн.)
2. Вероятность того, что предельная ошибка репрезентативности не превысит 0,3 грн., это значит
P{|
|≤0.3}
|
|≤0.3
Предельная ошибка репрезентативности .
Тогда, 0,3
; 0,3=t*0,24.; t=1,25.
Из таблицы, находим t=1,25 соответствует вероятность P=0.7887.
В этом случае генеральная средняя совокупность заключена в пределах:
299,7300,3 (грн.)
Вероятность того, что предельная ошибка репрезентативности не превышает 0,3 грн. равна P=0,7887.
Задача 7
По данным задачи 1 для изучения тесноты связи между среднегодовой стоимостью основных фондов и объемом товарной продукции определить коэффициент корреляции.
Решение
Обозначим через X –факторный признак, среднегодовую стоимость ОФ (млн. грн.), а Y- результативный признак, товарная продукция, (млн. грн.).
Сопоставив имеющиеся ряды X и Y найдем коэффициент корреляции.
| 1 | 2 | 3 | 4 | 5 | 6 |
| № завода | Среднегодовая стоимость ОФ, млн. грн. X | Товарная продукция, млн. грн. Y | X*Y, млн. грн. | X2, млн. грн. | Y2, млн. грн. |
| 1 | 3,0 | 3,2 | 9,6 | 9 | 10,24 |
| 2 | 7,0 | 9,6 | 67,2 | 49 | 92,16 |
| 3 | 2,0 | 1,5 | 3 | 4 | 2,25 |
| 4 | 3,9 | 4,2 | 16,38 | 15,21 | 17,64 |
| 5 | 3,3 | 6,4 | 21,12 | 10,89 | 40,96 |
| 6 | 2,8 | 2,8 | 7,84 | 7,84 | 7,84 |
| 7 | 6,5 | 9,4 | 61,1 | 42,25 | 88,36 |
| 8 | 6,6 | 11,9 | 78,54 | 43,56 | 141,61 |
| 9 | 2,0 | 2,5 | 5 | 4 | 6,25 |
| 10 | 4,7 | 3,5 | 16,45 | 22,09 | 12,25 |
| 11 | 2,7 | 2,3 | 6,21 | 7,29 | 5,29 |
| 12 | 3,3 | 1,3 | 4,29 | 10,89 | 1,69 |
| 13 | 3,0 | 1,4 | 4,2 | 9 | 1,96 |
| 14 | 3,1 | 3,0 | 9,3 | 9,61 | 9 |
| 15 | 3,1 | 2,5 | 7,75 | 9,61 | 6,25 |
| 16 | 3,5 | 7,9 | 27,65 | 12,25 | 62,41 |
| 17 | 3,1 | 3,6 | 11,16 | 9,61 | 12,96 |
| 18 | 5,6 | 8,0 | 44,8 | 31,36 | 64 |
| 19 | 3,5 | 2,5 | 8,75 | 12,25 | 6,25 |
| 20 | 4,0 | 2,8 | 11,2 | 16 | 7,84 |
| 21 | 7,0 | 12,9 | 90,3 | 49 | 166,41 |
| 22 | 1,0 | 1,6 | 1,6 | 1 | 2,56 |
| 23 | 4,5 | 5,6 | 25,2 | 20,25 | 31,36 |
| 24 | 4,9 | 4,4 | 21,56 | 24,01 | 19,36 |
| Итого | 94,1 | 114,8 | 560,2 | 429,97 | 816,9 |
Коэффициент корреляции определяется по формуле:
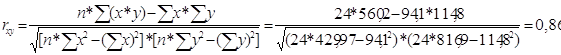
Вывод: Поскольку 0≤ rxy=0,86≤ 1, то это показывает прямую связь между среднегодовой стоимостью ОФ и товарной продукцией, т.е. увеличение X влечет за собой увеличение Y, причем близость коэффициента корреляции к 1 говорит о стремлении к функциональной зависимости, когда каждому значению факторного признака строго соответствует значение результата признака.
Литература
1. Конспект лекций по дисциплине «Статистика» для студентов экономических специальностей заочной формы обучения, 2000 г., Донецк
2. «Общая теория статистики», Учебник, М.Р. Ефимова, 2002 г., Москва
3. Методические указания по дисциплине «Статистика», Донецк
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... распределения генеральной совокупности F(x) и – эмпирической функция распределения Fn(x) , построенной по выборке х1,…,хn, называется функция. Теорема. Если F(x) непрерывна, то распределения статистики Колмогорова Dn не зависит от F(x). Условные математические ожидания и условные распределения. Св-ва условных мат. ожиданий. Аналоги формул полной вероятности и формулы Байеса для мат. ожиданий ГММЕ ...
... дает возможность статистического моделирования, происходящих в населении процессов. Потребность в моделировании возникает в случае невозможности исследования самого объекта. Наибольшее число моделей, применяемых в статистике населения, разработано для характеристики его динамики. Среди них выделяются экспоненциальные и логистические. Особое значение в прогнозе населения на будущие периоды имеют ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
0 комментариев