Навигация
Анализ 10% банковских счетов населения региона, выделенных в результате бесповторного собственно-случайного отбора, показал следующее распределение:
| Размер вклада, тыс. руб | До 1,0 | 1,0–5,0 | 5,0–10,0 | 10,0–15,0 | 15,0 и выше |
| Количество вкладов, % | 20,0 | 25,0 | 40,0 | 10,0 | 5,0 |
Определите.
1. Средний размер вклада.
2. С вероятностью Р=0,954 установите возможные пределы для всей совокупности вкладов населения:
а) среднего размера вклада;
б) доли вкладов до 5 тыс. руб.
в) общей суммы вкладов.
Сделайте выводы.
Решение
1. Средний размер вклада.
Составим расчётную таблицу, которая по сути есть ряд распределения.
| Интервал | Середина интервала | Количество вкладов, % |
| 0,0–1,0 | 0,05 | 20,0 |
| 1,0–5,0 | 3,0 | 25,0 |
| 5,0–10,0 | 7,5 | 40,0 |
| 10,0–15,0 | 12,5 | 10,0 |
| 15,0–20,0 | 17,5 | 5,0 |
Рассчитываем средний размер вклада.
хср=0,05*0,2+3,0*0,25+7,5*0,4+12,5*0,1+17,5*0,05=5,885 руб.
Или, приближённо, хср=6000 руб.
2. С вероятностью Р=0,954 установим возможные пределы для всей совокупности вкладов населения:
а) среднего размера вклада.
Предел ошибки рассчитывается по формуле:
Δ=t*μ; при вероятности Р=0,954 нормированное отклонение t=2 [стр. 36], то есть Δ=2*μ;
μ=![]() ; в нашем случае
; в нашем случае ![]() =10%, или
=10%, или ![]() =0,1
=0,1
Так как в задаче принимается N=100%, то n=10.
Находим дисперсию σ2:
σ2=![]()
![]()
σ2= ![]() (0,05–5,885)2*0,2+(3–5,885)2*0,25+(7,5–5,885)2*0,4+(12,5–5,885)2*0,1+
(0,05–5,885)2*0,2+(3–5,885)2*0,25+(7,5–5,885)2*0,4+(12,5–5,885)2*0,1+
+(17,5–5,885)2*0,05=21,05
Тогда μ=![]() =
=![]() =1,376
=1,376
Получаем: Δ=t*μ=2*1,376=2,752; получаем искомый интервал:
(5,885–2,752; 5,885+2,752), или генеральная средняя (средний размер вклада) лежит в интервале (3,133; 8,637) руб. с вероятностью 0,954.
б) С вероятностью Р=0,954 установим возможные пределы для доли вкладов до 5 тыс. руб.
Для доли имеем:
р=w±Δw – требуемая оценка.
Δ=t*μ, w=(20+25)/100=0,45=45,0%
При вероятности Р=0,954 нормированное отклонение t=2 [стр. 36].
Рассчитаем μ по формуле:
μ=![]() =
=![]() =0,222, или 22,2%.
=0,222, или 22,2%.
Получаем:
Δ=2*22,2%=44,4%
Тогда пределы, в которых будет находиться доля вкладов до 5 тыс. руб., составят (45,0–44,4; 45,0+44,4)%, или (0,6; 99,4)% – искомый интервал.
в) С вероятностью Р=0,954 установим возможные пределы для всей совокупности вкладов населения для общей суммы вкладов.
Для этого распространим выборочные данные на всю совокупность вкладов.
Так как генеральная средняя (средний размер вклада) лежит в интервале (3,133; 8,637) руб. с вероятностью 0,954, то для 100% населения сумма составит (3,133*100; 8,637*100), или (313,3; 863,7) рублей.
Сделаем выводы.
Средний размер вклада, равный 5,885 руб., лежит в интервале (3,133; 8,637) руб. с вероятностью 0,954. Доля вкладов менее 5000 руб. лежит в интервале (0,6; 99,4)%. Общая сумма вкладов находится в интервале (313,3; 863,7) рублей с вероятностью 0,954.
Задача 2Имеются следующие данные о потерях рабочего времени на предприятии вследствие заболеваемости с временной утратой трудоспособности.
| Год | Потери рабочего времени, чел.-дни |
| 1 | 933,4 |
| 2 | 904,0 |
| 3 | 965,0 |
| 4 | 1014,1 |
| 5 | 1064,8 |
| 6 | 1122,9 |
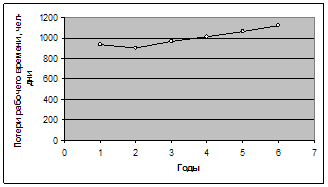
1. Для определения тенденции изменения потерь рабочего времени проведите аналитическое выравнивание (подберите вид аналитической функции).
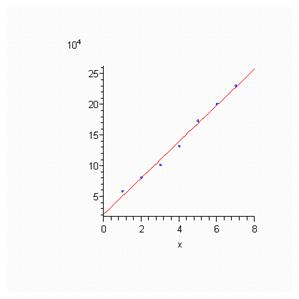
2. Отобразите фактические и теоретические (выровненные) уровни ряда на графике. Покажите ожидаемые уровни ряда на следующие 2–3 года, сделайте выводы.
Решение
Отобразим практические данные на графике.
Похожие работы
... технологических цепочек; применения общестатистических методов (корреляции, индексного, табличного, графического и др.) к новому объекту исследования — ФПГ. 2. Методика статистического анализа функционирования финансово-промышленной группы и ее технологических цепочек, включающая, разработанные на основе аддитивных, мультипликативных и смешанных моделей, алгоритмы статистического анализа ...
... с каждым годом увеличивается, за счет внедрения новых технологий, научного подхода к делу с помощью Иркутской Сельскохозяйственной Академии. 3. Экономико-статистический анализ себестоимости яиц 3.1. Статистическое наблюдение Статистическое наблюдение представляет собой планомерное, научно организованное и, как правило, систематическое собирание данных о явлениях и процессах общественной ...
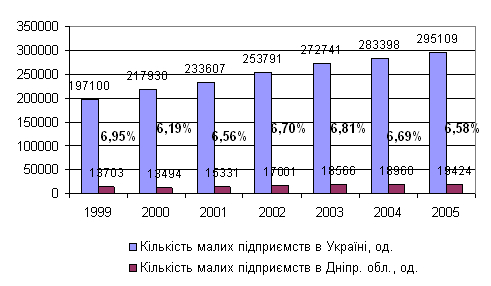
... зменшення розміру малих підприємств, а отже і показників їх фінансової стійкості та здатності вижити при економічних труднощах. Також середньомісячна заробітна плата працівників у середньому по області та на малих підприємствах суттєво різняться. З часом різниця збільшується. У 2005 році середньорічна заробітна плата на малих підприємствах області була вже вдвічі меншою за середньорічну заробітну ...
... полномочий; · методологическое и организационное обеспечение формирования показателей, характеризующих уровень достижения целей социально-экономического развития государства, и показателей деятельности федеральных органов исполнительной власти; · интеграцию статистических информационных ресурсов на основе методологической и технологической совместимости для эффективного их использования при ...
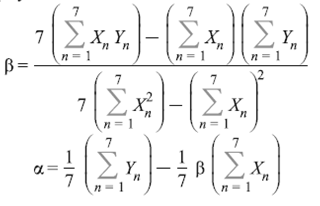
0 комментариев