Навигация
Для определения тенденции изменения потерь рабочего времени проведём аналитическое выравнивание (подберём вид аналитической функции)
1. Для определения тенденции изменения потерь рабочего времени проведём аналитическое выравнивание (подберём вид аналитической функции).
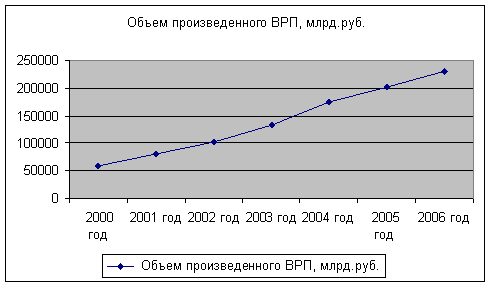
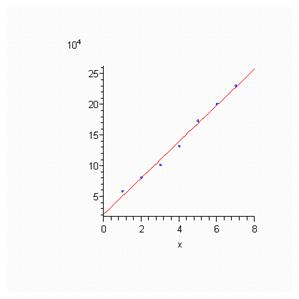
Из визуального анализа графика видно, что тенденцию потерь рабочего времени корректно представить в виде линейной функции. Найдём уравнение тренда с помощью Excel (для этого в меню «Параметры» выбираем: показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации R2):
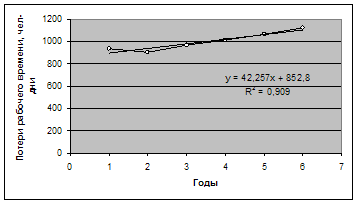
Уравнение тренда имеет вид: y=42,257*t+852,8
2. Отобразим фактические и теоретические (выровненные) уровни ряда на графике.
График отображён на рисунке выше. Выровненные уровни ряда представим в таблице (находим с помощью уравнения тренда).
| Год | Потери рабочего времени, чел.-дни | Выровненные уровни ряда. |
| 1 | 933,4 | 895,057 |
| 2 | 904,0 | 937,314 |
| 3 | 965,0 | 979,571 |
| 4 | 1014,1 | 1021,828 |
| 5 | 1064,8 | 1064,085 |
| 6 | 1122,9 | 1106,342 |
| 7 | 1148,599 | |
| 8 | 1190,856 | |
| 9 | 1233,113 |
Покажем ожидаемые уровни ряда на следующие 2–3 года (прогноз сделан в таблице и рассчитан по уравнению тренда). График:
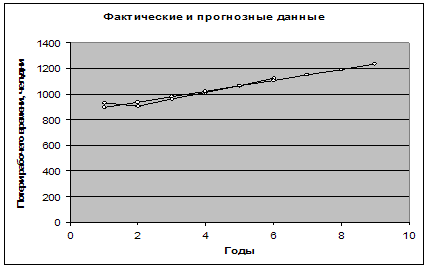
Сделаем выводы.
Представленные данные моделируются линейной функцией y=42,257x+852,8
С помощью уравнения получены прогнозные данные на три года вперёд: в 7 году потери рабочего времени составили 1148,599 человеко-дней; в 8 и 9 – 1190,856 и 1233,113 человеко-дней соответственно.
Задача 3Имеются следующие данные по предприятиям отрасли:
| Предприятия | Среднегодовая стоимость производственных фондов, тыс. руб. | Прибыль, тыс. руб. | ||
| Предыдущий год | Отчётный год | Предыдущий год | Отчётный год | |
| 1 | 10000 | 12500 | 2000 | 2400 |
| 2 | 7400 | 7800 | 1560 | 1820 |
Определите:
1) Индексы рентабельности производства для каждого предприятия в отдельности (индивидуальные индексы).
2) Индексы рентабельности производства:
а) переменного состава;
б) фиксированного состава;
в) структурных сдвигов.
Объясните различие полученных результатов. Покажите взаимосвязь исчисленных индексов.
Решение
1) Определим индексы рентабельности производства для каждого предприятия в отдельности (индивидуальные индексы).
Рентабельность рассчитывается по формуле:
R=![]()
Предприятие 1.
Базисный год. R01=2000/10000=0,2, или 20,0%
Отчётный год. R11=2400/12500=0,192, или 19,2%
Предприятие 2.
Базисный год. R02=1560/7400=0,211, или 21,1%
Отчётный год. R12=1820/7800=0,233, или 23,3%
Составим расчётную таблицу.
| Предприятие | Рентабельность, % | |
| Базисный год | Отчётный год | |
| 1 | 20,0 | 19,2 |
| 2 | 21,1 | 23,3 |
Индивидуальные индексы.
Предприятие 1.
IR1=19,2/20,0=0,960
Предприятие 2.
IR2=23,3/21,1=1,104
Получили индексы рентабельности производства для каждого предприятия в отдельности (индивидуальные индексы)
2) Определим индексы рентабельности производства.
| Предприятия | Среднегодовая стоимость производственных фондов, тыс. руб. | Прибыль, тыс. руб. | ||
| Предыдущий год | Отчётный год | Предыдущий год | Отчётный год | |
| 1 | 10000 | 12500 | 2000 | 2400 |
| 2 | 7400 | 7800 | 1560 | 1820 |
| Итого | 17400 | 20300 | 3560 | 4220 |
Составим расчётную таблицу
| Предприятия | Предыдущий год | Отчётный год | ||
| Среднегодовая стоимость производственных фондов, тыс. руб | Рентабельность, % | Среднегодовая стоимость производственных фондов, тыс. руб. | Рентабельность, % | |
| 1 | 10000 | 20,0 | 12500 | 19,2 |
| 2 | 7400 | 21,1 | 7800 | 23,3 |
| В целом | 17400 | 20,46 | 20300 | 20,79 |
Базисный год. R0=3560/17400=0,2046, или 20,46%
Отчётный год. R1=4220/20300=0,2079, или 20,79%
а) Определим индекс рентабельности производства переменного состава:
IRпер= R1/ R0=20,79/20,46=1,016
б) Определим индекс рентабельности производства фиксированного состава.
IRфикс=![]() =
=![]() =1,017
=1,017
в) Определим индекс рентабельности производства структурных сдвигов
IRстр= IRпер/ IRфикс=1,016/1,017=0,999
Объясним различие полученных результатов.
Индекс рентабельности производства переменного состава равен 1,016, этот индекс учитывает одновременно и влияние структурных изменений в составе совокупности, и изменение уровня качественного признака (рентабельности в нашем случае) у предприятий.
Индекс фиксированного состава равен 1,017, этот индекс учитывает только изменение уровня качественного признака (рентабельности) у предприятий. Индекс структурных сдвигов учитывает только влияние структурных изменений в составе совокупности.
Покажем взаимосвязь исчисленных индексов.
IRпер=IRфикс* IRстр, в нашем случае: 1,016=1,017*0,999
Задача 4Оцените тесноту линейной связи признаков «онкологическая заболеваемость» и «работа со свинцом».
| Работа со свинцом | Обследовано рабочих, чел. | ||
| Всего | В том числе | ||
| Больные онкозаболеваемостью | Здоровые | ||
| Да | 36 | 28 | 8 |
| Нет | 144 | 62 | 82 |
| Итого | 180 | 90 | 90 |
Решение
В нашем случае необходимо рассчитать коэффициенты сопряжённости – коэффициент контингенции и коэффициент ассоциации.
Методика расчёта следующая.
| Факторный признак | Результативный признак | ||
| В том числе | Итого | ||
| F | G | ||
| А | a | b | a+b |
| В | c | d | c+d |
| Итого | a+c | b+d | n |
Коэффициент контингенции:
КК=![]() ; КК=
; КК=![]() =
=![]() =
=![]() =0,278
=0,278
Коэффициент ассоциации:
КА=![]() ;
;
КА=![]() =
=![]() =0,645
=0,645
Видно, что связь присутствует, и достаточно заметная.
Задача 5Имеются следующие данные по экономике страны (млрд. руб.):
| Выпуск продуктов в основных ценах | 3900 |
| Выпуск рыночных услуг (за исключением условно исчисленных услуг финансовых посредников) | 1100 |
| Выпуск не рыночных услуг | 900 |
| Налоги на продукты и услуги | 790 |
| Прочие косвенные налоги | 310 |
| Экспорт товаров и услуг | 430 |
| Импорт товаров и услуг | 350 |
| Проценты, полученные банками по ссудам | 290 |
| Проценты, уплаченные банками за пользование средствами | 165 |
| Субсидии на импорт | 45 |
| Материальные затраты на производство продуктов и услуг в течение года | 2175 |
| -износ основных средств | 405 |
| -недоамортизированная стоимость выбывших основных средств | 45 |
| Прочие элементы промежуточного потребления (за исключением условно исчисленной продукции банков) | 90 |
Определите валовой внутренний продукт в рыночных ценах.
Решение
Валовой внутренний продукт страны (ВВП) характеризует стоимость конечных товаров и услуг, произведённых резидентами и нерезидентами за отчётный период.
ВВП=∑ВВ-∑ПП+∑ЧН+(Э-И)+Δ(%)
ВВ – выпуск товаров и услуг.
ПП – промежуточное потребление.
ЧН – чистые налоги на продукты.
И – импорт.
Э – экспорт.
Δ(%) – разница полученных и уплаченных процентов банками.
Рассчитаем следующие показатели.
1. ВВ=3900+1100+900=5900 млрд. руб.
2. Промежуточное потребление (ПП):
ПП=2175 + 405 + 45+90=2715 млрд. руб.
3. Чистые налоги на продукты (ЧН):
ЧН=Н-С=790+310 – 45=1055 млрд. руб.
4. (Э-И)=430–350=80 млрд. руб.
5. Δ(%)=290–165=125 млрд. руб.
Тогда ВВП=5900 – 2715+1055+80+125=4445 млрд. руб.
Задача 6Имеются следующие данные о распределении населения региона по 10% группам населения по уровню среднедушевого дохода.
| Базисный | Отчётный | |
| Денежные доходы – всего | 100,0 | 100,0 |
| В том числе по 10 – процентным группам населения | ||
| Первая (с наименьшими доходами) | 2,3 | 2,1 |
| Вторая | 3,7 | 3,3 |
| Третья | 5,2 | 4,2 |
| Четвёртая | 6,4 | 5,8 |
| Пятая | 7,6 | 7,2 |
| Шестая | 10,0 | 8,9 |
| Седьмая | 12,2 | 8,9 |
| Восьмая | 14,3 | 12,5 |
| Девятая | 16,7 | 21,4 |
| Десятая (с наибольшими доходами) | 21,6 | 25,7 |
Определите коэффициенты дифференциации доходов (коэффициент фондов), концентрации доходов Джини. Постройте график Лоренца.
Сделайте выводы.
Решение
Определим коэффициент дифференциации доходов (коэффициент фондов)
Кф=![]()
Базисный год: Кф0=![]() =
=![]() =9,391; отчётный год: Кф1=
=9,391; отчётный год: Кф1=![]() =
=![]() =12,238
=12,238
Определим коэффициент концентрации доходов Джини.
Рассчитывается по формуле:
G=1–2*![]() ,
,
где сum yi – кумулятивная доля дохода (накопленная частость).
Коэффициент G изменяется в пределах от 0 до 1. Чем ближе его значение к 1, тем выше уровень неравенства (концентрации) в распределении, чем ближе к 0, тем выше уровень равенства.
Базисный год
| Группа населения | Доля населения, xi | Доля в совокупном доходе, yi | Расчётные показатели | ||
| Sum yi | xi*yi | xi*Sum yi | |||
| 1 | 0,1 | 0,023 | 0,023 | 0,0023 | 0,0023 |
| 2 | 0,1 | 0,037 | 0,06 | 0,0037 | 0,006 |
| 3 | 0,1 | 0,052 | 0,112 | 0,0052 | 0,0112 |
| 4 | 0,1 | 0,064 | 0,176 | 0,0064 | 0,0176 |
| 5 | 0,1 | 0,076 | 0,252 | 0,0076 | 0,0252 |
| 6 | 0,1 | 0,1 | 0,352 | 0,01 | 0,0352 |
| 7 | 0,1 | 0,122 | 0,474 | 0,0122 | 0,0474 |
| 8 | 0,1 | 0,143 | 0,617 | 0,0143 | 0,0617 |
| 9 | 0,1 | 0,167 | 0,784 | 0,0167 | 0,0784 |
| 10 | 0,1 | 0,216 | 1,000 | 0,0216 | 0,1000 |
| Всего | 1,0 | 1,000 | 0,1000 | 0,385 | |
Коэффициент К. Джини равен:
G=1–2*![]() =1–2*0,385+0,1=0,33
=1–2*0,385+0,1=0,33
Отчётный год
| Группа населения | Доля населения, xi | Доля в совокупном доходе, yi | Расчётные показатели | ||
| Sum yi | xi*yi | xi*Sum yi | |||
| 1 | 0,1 | 0,021 | 0,021 | 0,0021 | 0,0021 |
| 2 | 0,1 | 0,033 | 0,054 | 0,0033 | 0,0054 |
| 3 | 0,1 | 0,042 | 0,096 | 0,0042 | 0,0096 |
| 4 | 0,1 | 0,058 | 0,154 | 0,0058 | 0,0154 |
| 5 | 0,1 | 0,072 | 0,226 | 0,0072 | 0,0226 |
| 6 | 0,1 | 0,089 | 0,315 | 0,0089 | 0,0315 |
| 7 | 0,1 | 0,089 | 0,404 | 0,0089 | 0,0404 |
| 8 | 0,1 | 0,125 | 0,529 | 0,0125 | 0,0529 |
| 9 | 0,1 | 0,214 | 0,743 | 0,0214 | 0,0743 |
| 10 | 0,1 | 0,257 | 1,000 | 0,0257 | 0,1 |
| Всего | 1,0 | 1 | 0,1000 | 0,3542 | |
Коэффициент К. Джини равен:
G=1–2*![]() =1–2*0,3542+0,1=0,3916
=1–2*0,3542+0,1=0,3916
Построим график Лоренца.
| % населения | Базисный период | Отчётный период. | ||||
| Доля дохода | Накопленная доля дохода при равенстве X0 | Накопленная доля дохода фактически Y0 | Доля дохода | Накопленная доля дохода при равенстве X1 | Накопленная доля дохода фактически Y1 | |
| 0,1 | 0,023 | 0,1 | 0,023 | 0,021 | 0,1 | 0,021 |
| 0,1 | 0,037 | 0,2 | 0,06 | 0,033 | 0,2 | 0,054 |
| 0,1 | 0,052 | 0,3 | 0,112 | 0,042 | 0,3 | 0,096 |
| 0,1 | 0,064 | 0,4 | 0,176 | 0,058 | 0,4 | 0,154 |
| 0,1 | 0,076 | 0,5 | 0,252 | 0,072 | 0,5 | 0,226 |
| 0,1 | 0,1 | 0,6 | 0,352 | 0,089 | 0,6 | 0,315 |
| 0,1 | 0,122 | 0,7 | 0,474 | 0,089 | 0,7 | 0,404 |
| 0,1 | 0,143 | 0,8 | 0,617 | 0,125 | 0,8 | 0,529 |
| 0,1 | 0,167 | 0,9 | 0,784 | 0,214 | 0,9 | 0,743 |
| 0,1 | 0,216 | 1,0 | 1,0 | 0,257 | 1,0 | 1,0 |
Базисный год
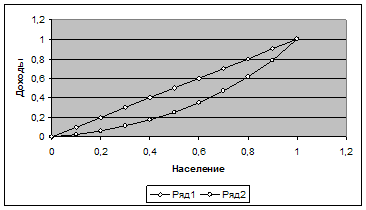
Ряд 1 – линия равномерного распределения, ряд 2 – линия фактического распределения (кривая Лоренца)
Отчётный год

Ряд 1 – линия равномерного распределения, ряд 2 – линия фактического распределения (кривая Лоренца)
Сделаем выводы.
Дифференциация доходов населения в отчётном году выросла по сравнению с базисным с 9,391 до 12,238; это говорит об увеличении неравенства доходов населения. Коэффициенты К. Джини составили 0,33 и 0,3916 соответственно в базисном и отчётном годах; это подтверждает увеличение неравенства доходов. Такой же вывод можно сделать из визуального анализа графиков М. Лоренца: неравномерность доходов увеличивается (заметен крен кривой линии вправо).
Задача 7Предприятие работает с 25 сентября. Численность работников списочного состава была следующей: 25 сентября (вторник) – 180 чел., 26 сентября (среда) – 185 чел., 27 сентября (четверг) – 200 чел., 28 сентября (пятница) – 210 чел. Последние два дня месяца приходились на выходные дни.
Кроме того, известно, что число совместителей с 25 по 27 – 5 чел.; с 28 по 30 – 7 чел., а число работающих по договорам гражданско – правового характера с 25 по 27 сентября – 10 чел.; и с 28 по 30 – 12 чел. среднесписочная численность за октябрь – 180 чел., за ноябрь – 175 чел. В декабре число явок на работу составило 3960 человеко – дней, число неявок по всем причинам 1800 человеко – дней.
Определите среднесписочную численность работников за год.
Решение
Средняя списочная численность работников рассчитывается по формуле:
![]() ,
,
где Т – списочная численность за каждый календарный день месяца (численность в праздники и выходные приравнивается к численности предыдущего дня); Дкал – число календарных дней в месяце – независимо от того, работало предприятие или нет. Аналогично рассчитывается списочная численность лиц, работающих по договорам гражданско – правового характера.
Средняя списочная численность совместителей, а также лиц, работавших неполное рабочее время, определяется пропорционально отработанному ими времени. Расчётная формула.
![]()
Определяем среднесписочную численность персонала предприятия за сентябрь.
| Число | Численность |
| 25.09 | 180 |
| 26.09 | 185 |
| 27.09 | 200 |
| 28.09 | 210 |
| 29.09 | 210 |
| 30.09 | 210 |
![]() =
=![]() =
=![]() =39,8=40 человек
=39,8=40 человек
Определяем среднесписочную численность совместителей за сентябрь.
| Число | Численность |
| 25.09 | 5 |
| 26.09 | 5 |
| 27.09 | 5 |
| 28.09 | 7 |
| 29.09 | 7 |
| 30.09 | 7 |
Т=(3*0,5*5+3*0,5*7)/6=18/6=3 человека
Определяем среднесписочную численность лиц, работающих по договорам гражданско – правового характера, за сентябрь.
| Число | Численность |
| 25.09 | 10 |
| 26.09 | 10 |
| 27.09 | 10 |
| 28.09 | 12 |
| 29.09 | 12 |
| 30.09 | 12 |
![]() =
=![]() =
=![]() =2,2=2 человека
=2,2=2 человека
Определяем среднесписочную численность всех работников предприятия за декабрь.
В декабре число явок на работу составило 3960 человеко – дней, число неявок по всем причинам 1800 человеко – дней.
То есть, всего в декабре 3960 +1800=5760 человеко – дней.
Учтём, что в декабре 31 день, получим среднюю численность: 5760/31=185,8 человек=186 человек.
Сведём полученные данные в таблицу
| Месяц | Среднесписочная численность | |||
| Персонала | Совместителей | По договорам | Сумма | |
| Сентябрь | 40 | 3 | 2 | 45 |
| Октябрь | 180 | 180 | ||
| Ноябрь | 175 | 175 | ||
| Декабрь | 186 | 186 | ||
В итоге получаем:
Тср.сп=(45+180+175+186)/4=147 человек.
Список использованной литературы
1. Гусаров В.М. Статистика: Учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001.
2. Сборник задач по теории статистики: Учебное пособие/ Под ред. проф. В.В. Глинского и к.э.н., доц. Л.К. Серга. Изд.З-е. – М.:ИНФРА-М; Новосибирск: Сибирское соглашение, 2002.
3. Статистика: Учебное пособие / Харченко Л-П., Долженкова В.Г., Ионин В.Г. и др., Под ред. В.Г. Ионина. – Изд. 2-е, перераб. и доп. – М.: ИНФРА-М.2003.
4. Теория статистики: Учебник / Под ред. Р.А. Шмойловой, – М. – .Финансы и статистика, 2000.
5. Экономика и статистика фирм: Учебник /В.Е. Адамов, С.Д. Ильенкова, Т.П. Сиротина; под ред. С.Д. Ильенковой. – 2-е изд. – М.: Финансы и статистика, 1997.
Похожие работы
... технологических цепочек; применения общестатистических методов (корреляции, индексного, табличного, графического и др.) к новому объекту исследования — ФПГ. 2. Методика статистического анализа функционирования финансово-промышленной группы и ее технологических цепочек, включающая, разработанные на основе аддитивных, мультипликативных и смешанных моделей, алгоритмы статистического анализа ...
... с каждым годом увеличивается, за счет внедрения новых технологий, научного подхода к делу с помощью Иркутской Сельскохозяйственной Академии. 3. Экономико-статистический анализ себестоимости яиц 3.1. Статистическое наблюдение Статистическое наблюдение представляет собой планомерное, научно организованное и, как правило, систематическое собирание данных о явлениях и процессах общественной ...
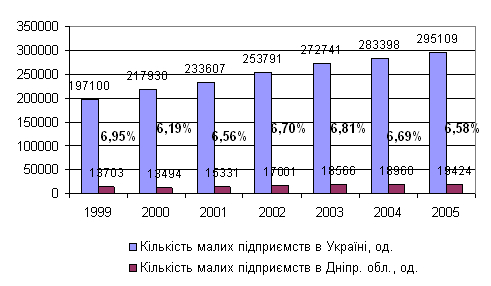
... зменшення розміру малих підприємств, а отже і показників їх фінансової стійкості та здатності вижити при економічних труднощах. Також середньомісячна заробітна плата працівників у середньому по області та на малих підприємствах суттєво різняться. З часом різниця збільшується. У 2005 році середньорічна заробітна плата на малих підприємствах області була вже вдвічі меншою за середньорічну заробітну ...
... полномочий; · методологическое и организационное обеспечение формирования показателей, характеризующих уровень достижения целей социально-экономического развития государства, и показателей деятельности федеральных органов исполнительной власти; · интеграцию статистических информационных ресурсов на основе методологической и технологической совместимости для эффективного их использования при ...
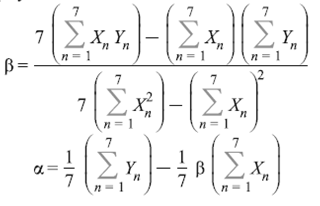
0 комментариев