Статистический анализ выборочного наблюдения

Федеральное агентство по образованию

Кафедра Экономики и финансов

Южно-Уральского Государственного Университета

Статистический анализ выборочного наблюдения

Пояснительная записка к курсовой работе

по курсу «Статистика»

вариант 104

Руководитель

Серебренникова Т.А.

«____»___________2005г.

______________________

Автор проекта

студент группы ЗЭиУ-427

Михайлов А.А.

«____»___________2005г.

______________________

Проект защищен

с оценкой

______________________

«_____»___________2005г.

Челябинск

2005

Аннотация

Михайлов А.А. Статистический анализ выборочного наблюдения. – Челябинск: ЮУрГУ, ЗЭиУ, 2005, 27 с., 5 ил., 11 табл.. Список литературы – 2 наименования.

В данном курсовом проекте исследуется показатель «Площади жилищ, приходящейся в среднем на одного жителя, по регионам Российской Федерации, весь жилищный фонд; кв.м./чел» на конец 2003г., охватываются такие разделы, как «Сводка и группировка данных», «Вариационный анализ», «Выборочное наблюдение», «Ряды динамики».

Применяются различные методы статистики для вычисления показателей. Производится анализ полученных результатов в каждом разделе. Результатом выполнения курсовой работы является умение и навыки работы со статистическими данными

Содержание

Введение

1.         1.Сводка и группировка данных статистического наблюдения

2.         Вариационный анализ

3.         Выборочное наблюдение

4.         Анализ динамики

Заключение

Список литературы

Введение

Многие окружающие нас процессы можно выразить с помощью числовых значений. Однако этих чисел оказывается так много и они носят различный характер, что для обыденного человека не представляют никакой информации. Методы статистики позволяют анализировать такие данные, находить закономерности и даже строить прогнозы.

Основываясь на статистических данных, мы можем предсказывать развитие различных ситуаций. Что помогает нам как в технике, так и в управленческой деятельности при принятии различных решений. Именно поэтому знание основных методов статистики необходимо для того, чтобы успешно решать различного рода задачи.

Количество данных, поступающих к нам из внешнего мира, постоянно растет, поэтому статистические методы, применяемые для упорядочивания этих данных, представления их в удобном для рассмотрения и анализа виде, никогда не теряют своей актуальности.

1.   Сводка и группировка данных статистического наблюдения

Выполним простую сводку по показателю «Площадь жилищ, приходящаяся в среднем на одного жителя, по регионам Российской Федерации, весь жилищный фонд; кв.м/чел» на конец 2003г. Результат сводки представим в таблице 1.1

Таблица 1.1 – Простая сводка по показателю «Площадь жилищ, приходящаяся в среднем на одного жителя, по регионам Российской Федерации, весь жилищный фонд» на конец 2003г.

Название субъекта РФ	Площадь жилищ, кв.м/чел
Российская Федерация	20,2
Центральный федеральный округ	21,5
Белгородская область	22,0
Брянская область	21,9
Владимирская область	22,4
Воронежская область	22,9
Ивановская область	21,5
Калужская область	22,2
Костромская область	22,8
Курская область	22,0
Липецкая область	21,9
Московская область	23,3
Орловская область	21,2
Рязанская область	22,5
Смоленская область	22,8
Тамбовская область	21,6
Тверская область	24,5
Тульская область	22,5
Ярославская область	21,5
г. Москва	18,8
Северо-Западный федеральный округ	22,0
Республика Карелия	21,8
Республика Коми	22,2
Архангельская область	22,5
Вологодская область	23,1
Калининградская область	19,2
Ленинградская область	23,3
Мурманская область	22,3
Новгородская область	23,7
Псковская область	24,5
г. Санкт-Петербург	20,9
Южный федеральный округ	18,4
Республика Адыгея	22,7
Республика Дагестан	15,6
Республика Ингушетия	6,7
Чеченская Республика	...
Кабардино-Балкарская Республика	15,3
Республика Калмыкия	19,8
Карачаево-Черкесская Республика	18,4
Республика Северная Осетия - Алания	24,9
Краснодарский край	18,7
Ставропольский край	19,1
Астраханская область	18,6
Волгоградская область	19,4
Ростовская область	19,1
Приволжский федеральный округ	19,9
Республика Башкортостан	18,6
Республика Марий Эл	20,2
Республика Мордовия	21,1
Республика Татарстан	19,7
Удмуртская Республика	18,1
Чувашская Республика	19,8
Кировская область	20,3
Нижегородская область	21,3
Оренбургская область	19,1
Пензенская область	21,3
Пермская область	18,9
Самарская область	20,0
Саратовская область	21,7
Ульяновская область	20,8
Уральский федеральный округ	19,5
Курганская область	19,1
Свердловская область	20,4
Тюменская область	18,3
Ямало-Ненецкий автономный округ	17,4
Челябинская область	19,8
Сибирский федеральный округ	19,0
Республика Алтай	15,2
Республика Бурятия	17,6
Республика Тыва	12,6
Республика Хакасия	18,9
Алтайский край	19,2
Красноярский край	20,0
Эвенкийский автономный округ	27,5
Иркутская область	19,3
Кемеровская область	19,7
Новосибирская область	18,6
Омская область	19,5
Томская область	19,0
Читинская область	18,2
Дальневосточный федеральный округ	19,8
Республика Саха (Якутия)	19,5
Приморский край	18,9
Хабаровский край	19,5
Амурская область	19,6
Камчатская область	21,2
Магаданская область	25,7
Сахалинская область	21,4
Еврейская автономная область	20,0
Чукотский автономный округ	28,4

Проанализировав все данные можно выделить две республики, данные по которым значительно отличаются от всей совокупности. Вследствие этого, уберем из расчетов Чеченскую республику и республику Ингушетия.

Построим простую группировку, с выделением групп субъектов со значением показателя выше и ниже среднего по Российской Федерации.

Рассчитаем среднее по группе, расчет выполним как простую арифметическую величину по формуле (1):

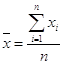, кв.м/чел (1)

где n – число субъектов РФ в данной группе,

X_i – значение по каждому субъекту.

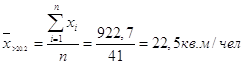
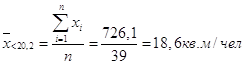
Результат занесем в таблицу 1.2.

Таблица 1.2 – Простая группировка с выделением групп субъектов выше и ниже среднего по Российской Федерации относительно среднего значения по России

Площадь жилищ, кв.м/чел	Количество субъектов	В % к общему числу	Среднее по группе, кв.м/чел
Ниже среднего по РФ (< 20,2 кв.м/чел)	39	48,75	18,6
Выше среднего по РФ (> 20,2 кв.м/чел)	41	51,25	22,5
Итого	80	100,00	20,2

Отобразим полученные результаты на графике, показанном на рисунке 1.1, для простой группировки лучшим образом подойдет круговая диаграмма.

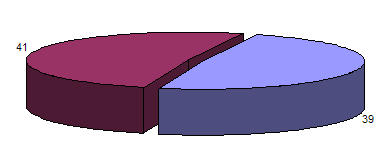
Рисунок 1.1 – Доля субъектов со значением выше и ниже среднего по Российской Федерации

Построим простую группировку, с выделением групп субъектов со значением показателя выше и ниже среднего относительно Челябинской области.

Рассчитаем среднее по группе, расчет выполним как простую арифметическую величину по формуле (1).

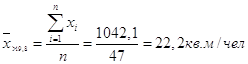
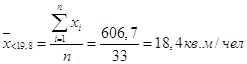
Результат занесем в таблицу 1.3.

Таблица 1.3 – Простая группировка с выделением групп субъектов выше и ниже среднего относительно Челябинской области

Площадь жилищ, кв.м/чел	Количество субъектов	В % к общему числу	Среднее по группе, кв.м/чел
Ниже среднего по ЧО (< 19,8 кв.м/чел)	33	41,25	18,4
Выше среднего по ЧО (> 19,8 кв.м/чел)	47	58,75	22,2
Итого	80	100,00	20,2

Отобразим полученные результаты на графике, показанном на рисунке 1.2. Для простой группировки лучшим образом подойдет круговая диаграмма.

Рисунок 1.2 – Доля субъектов со значением выше и ниже среднего по Челябинской области

Выполнив простые группировки видно, что в среднем значение показателя по РФ не сильно варьируется. Это обусловлено тем, что в каждом субъекте соотношение жителей и жилой площади сопоставимо. Поэтому разброс значений показателя не велик.