Навигация
3. Выборочное наблюдение
Произведем отбор 27 и 35 субъектов из генеральной совокупности.
Будем производить случайный отбор субъектов РФ.
Составим две таблицы из 27 и 35 субъектов соответственно 3.1 и 3.2.
Таблица 3.1 – Бесповторная выборка 27 субъектов РФ
| № п/п | Название субъекта | Площадь жилищ, кв.м/чел | |
| 1 | Владимирская область | 22,4 | |
| 2 | Ивановская область | 21,5 | |
| 3 | Костромская область | 22,8 | |
| 4 | Липецкая область | 21,9 | |
| 5 | Республика Карелия | 21,8 | |
| 6 | Архангельская область | 22,5 | |
| 7 | Калининградская область | 19,2 | |
| 8 | Мурманская область | 22,3 | |
| 9 | Краснодарский край | 18,7 | |
| 10 | Ставропольский край | 19,1 | |
| 11 | Астраханская область | 18,6 | |
| 12 | Волгоградская область | 19,4 | |
| 13 | Республика Башкортостан | 18,6 | |
| 14 | Республика Мордовия | 21,1 | |
| 15 | Удмуртская Республика | 18,1 | |
| 16 | Кировская область | 20,3 | |
| 17 | Курганская область | 19,1 | |
| 18 | Свердловская область | 20,4 | |
| 19 | Магаданская область | 25,7 | |
| 20 | Ямало-Ненецкий автономный округ | 17,4 | |
| 21 | Челябинская область | 19,8 | |
| 22 | Республика Алтай | 15,2 | |
| 23 | Республика Тыва | 12,6 | |
| 24 | Алтайский край | 19,2 | |
| 25 | Иркутская область | 19,3 | |
| 26 | Хабаровский край | 19,5 | |
| 27 | Сахалинская область | 21,4 | |
Таблица 3.2 – Бесповторная выборка 35 субъектов РФ
| № п/п | Название субъекта | Площадь жилищ, кв.м/чел | |
| 1 | Белгородская область | 22,0 | |
| 2 | Брянская область | 21,9 | |
| 3 | Воронежская область | 22,9 | |
| 4 | Калужская область | 22,2 | |
| 5 | Курская область | 22,0 | |
| 6 | Республика Коми | 22,2 | |
| 7 | Вологодская область | 23,1 | |
| 8 | Ленинградская область | 23,3 | |
| 9 | Новгородская область | 23,7 | |
| 10 | Псковская область | 24,5 | |
| 11 | Республика Адыгея | 22,7 | |
| 12 | Республика Дагестан | 15,6 | |
| 13 | Республика Калмыкия | 19,8 | |
| 14 | Карачаево-Черкесская Республика | 18,4 | |
| 15 | Ростовская область | 19,1 | |
| 16 | Республика Марий Эл | 20,2 | |
| 17 | Республика Татарстан | 19,7 | |
| 18 | Нижегородская область | 21,3 | |
| 19 | Пензенская область | 21,3 | |
| 20 | Ямало-Ненецкий автономный округ | 17,4 | |
| 21 | Челябинская область | 19,8 | |
| 22 | Самарская область | 20,0 | |
| 23 | Курганская область | 19,1 | |
| 24 | Свердловская область | 20,4 | |
| 25 | Тюменская область | 18,3 | |
| 26 | Республика Бурятия | 17,6 | |
| 27 | Республика Хакасия | 18,9 | |
| 28 | Кемеровская область | 19,7 | |
| 29 | Новосибирская область | 18,6 | |
| 30 | Томская область | 19,0 | |
| 31 | Приморский край | 18,9 | |
| 32 | Амурская область | 19,6 | |
| 33 | Еврейская автономная область | 20,0 | |
| 34 | Камчатская область | 21,2 | |
| 35 | Республика Саха (Якутия) | 19,5 | |
Посчитаем выборочные средние для двух выборок:
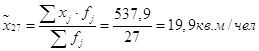
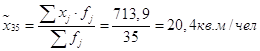
Найдем дисперсию для обеих выборок:
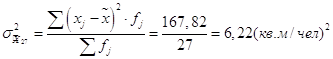
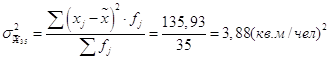
Для определения предельной ошибки возьмем вероятность попадания в интервал 0,99. По таблице в приложении 2, 3 страница 34-37 /1/, найдем значение коэффициента t = 2,58 и tСт=2,779. Подставим значения и посчитаем предельные ошибки для обоих случаев:
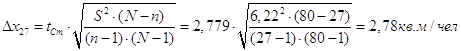
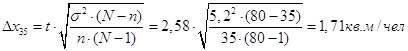
Таким образом, генеральная средняя будет лежать в пределах:
· при малой выборке: ![]()
· при большой выборке: ![]()
По заданию необходимо определить доверительный интервал генеральной средней по выборочным данным с вероятностью 0,689; 0,789; 0,889; 0,959. Для этого необходимо из таблиц приложений /1/ выписать соответствующие значения коэффициентов t и tСт. Подставим значения в формулы и посчитаем, а результаты занесем в таблицы 3.3 и 3.4 для малой выборки и большой соответственно.
Таблица 3.3 – Определение доверительных интервалов генеральной средней для заданных вероятностей для малой (27 субъектов) выборки
| Заданная вероятность | Значение tСт | Значение предельной ошибки, кв.м/чел | Доверительный интервал, кв.м/чел |
| 0,689 | 1,058 | 1,06 | [18,34; 20,46] |
| 0,789 | 1,315 | 1,31 | [18,09; 20,71] |
| 0,889 | 1,706 | 1,70 | [17,70; 21,10] |
| 0,959 | 2,479 | 2,48 | [16,92; 21,88] |
Таблица 3.4 – Определение доверительных интервалов генеральной средней для заданных вероятностей для большой (35 субъектов) выборки
| Заданная вероятность | Значение t | Значение предельной ошибки, кв.м/чел | Доверительный интервал, кв.м/чел |
| 0,689 | 1,01 | 0,67 | [19,73; 21,07] |
| 0,789 | 1,25 | 0,83 | [19,57; 21,23] |
| 0,889 | 1,60 | 1,06 | [19,34; 21,46] |
| 0,959 | 2,05 | 1,36 | [19,04; 21,76] |
Как мы видим, в обеих выборках выборочная средняя величина лежит довольно близко к генеральному среднему. Однако в большей выборке выборочная средняя гораздо ближе к генеральному среднему, это связано с тем, что большая выборка более точная.
Для всех заданных вероятностей значение генеральной средней лежит в доверительном интервале. Это свидетельствует о том, что нами был выбран правильный способ отбора регионов для оценки.
Доверительные интервалы для обеих выборок имеют разную длину из-за получившейся большой выборочной дисперсии в первой (малой) выборке. В целом, мы видим, что при увеличении доверительной вероятности доверительный интервал расширяется и в том и другом случае – мы можем гарантировать, что больший доверительный интервал будет иметь внутри себя генеральную среднюю с высокой вероятностью.
Похожие работы
... нормального распределения равны нулю: и . Вероятность попадания нормально распределенной случайной величины Х в заданный интервал (х1; х2) определяется по формуле (1): , (13) где Ф(х) – функция Лапласа, . (14) 4. Статистический анализ выборочной совокупности Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов. Объемом n выборочной ...
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... данных и по внедрению накопленного арсенала современных методов прикладной статистики. По нашему мнению, широкого внедрения заслуживают, в частности, методы многомерного статистического анализа, планирования эксперимента, статистики объектов нечисловой природы. Очевидно, рассматриваемые работы должны быть плановыми, организационно оформленными, проводиться мощными самостоятельными организациями и ...
... вида выборочного наблюдения; 6) установление сроков проведения наблюдения; 7) определение потребности в кадрах для проведения выборочного наблюдения, их подготовка; 8) оценка точности и достоверности данных выборки, определение порядка их распространения на генеральную совокупность. Представление о статистических данных, как о выборочных, может относиться не только к собственно выборке, но и ...
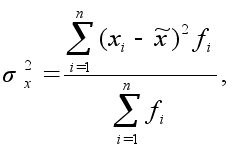
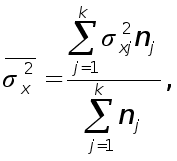
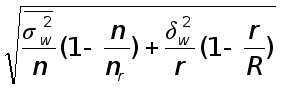
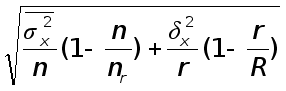
0 комментариев