Навигация
2. Вариационный анализ
Выполним вариационный анализ показателя «Площадь жилищ, приходящаяся в среднем на одного жителя, по регионам Российской Федерации, весь жилищный фонд» на конец 2003г.
Для этого построим вариационный ряд. Так как признак непрерывный, то необходимо разбить все значения на интервалы. Количество интервалов примерно можно определить с помощью формулы Стержесса:
![]() (2)
(2)
где k – количество интервалов,
n – количество субъектов РФ, попадающих в вариационный анализ.
Длину интервалов считаем по формуле (3):
![]() , кв.м/чел
(3)
, кв.м/чел
(3)
Подставим значения и посчитаем количество интервалов и шаг интервалов.
![]()
Примем k = 8.
![]() кв.м/чел
кв.м/чел
Так как в вариационном ряду встречаются максимальные и минимальные значения отличные от общей вариации, посчитаем другую длину интервала.
![]() кв.м/чел
кв.м/чел
Примем длину интервала l = 1,5 кв.м/чел.
Исходя из полученных интервалов и длины построим таблицу 2.1
Отобразим вариационный ряд графически. Для отображения вариационного ряда наиболее подходящим графиком является гистограмма. Построим гистограмму рисунок 2.1 по полученным значениям.
Таблица 2.1 – Распределение количества субъектов РФ
| Площадь жилищ, кв.м/чел | Количество субъектов |
| < 15,0 | 1 |
| 15,0 – 16,5 | 3 |
| 16,5 – 18,0 | 2 |
| 18,0 – 19,5 | 22 |
| 19,5 – 21,0 | 16 |
| 21,0 – 22,5 | 19 |
| 22,5 – 24,0 | 11 |
| > 24,0 | 6 |
| Итого | 80 |
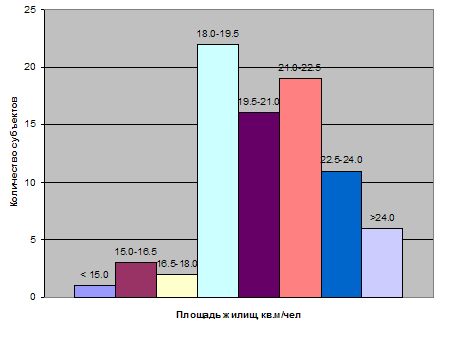
Рисунок 2.1 – Гистограмма распределения числа субъектов РФ в зависимости от площади жилищ, приходящейся на одного жителя
Построим кумуляту и огиву на рисунке 2.2, для этого составим таблицу 2.2 накопленных частот для кумуляты и огивы.
Таблица 2.2 – Накопленные значения для кумуляты и огивы
| Площадь жилищ, кв.м/чел | Количество субъектов | Накопленные частоты для кумуляты | Накопленные частоты для огивы |
| < 15,0 | 1 | 1 | 80 |
| 15,0 – 16,5 | 3 | 4 | 79 |
| 16,5 – 18,0 | 2 | 6 | 76 |
| 18,0 – 19,5 | 22 | 28 | 74 |
| 19,5 – 21,0 | 16 | 44 | 52 |
| 21,0 – 22,5 | 19 | 63 | 36 |
| 22,5 – 24,0 | 11 | 74 | 17 |
| > 24,0 | 6 | 80 | 6 |
| Итого | 80 | - | - |
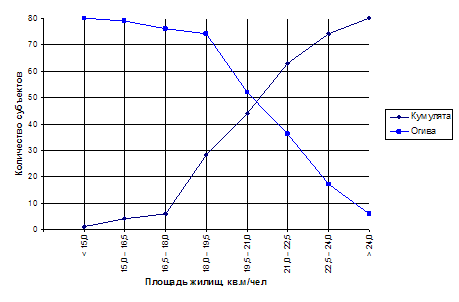
Рисунок 2.2 – Кумулята и огива распределения количества субъектов
Выполним расчет числовых характеристик показателя.
Необходимо рассчитать среднее значение вариационного ряда. Для интервального ряда среднее значение ряда считается по формуле (4):
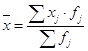 (4)
(4)
где xi – центр интервала,
fi – количество единиц в j-том интервале.
Подставим значения в формулу (4) и получим: ![]()
Для характеристики структуры вариационного ряда рассчитаем моду и медиану, они рассчитываются по формулам (5) и (6) соответственно:
![]() (5)
(5)
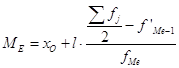 (6)
(6)
Подставим значения и получим:
![]() ,
, ![]()
Оценим также силу и размах вариации, они рассчитываются по формулам (7), (8), (9):
![]() (7)
(7)
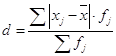 (8)
(8)
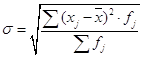 (9)
(9)
Подставим значения в формулы и получим:
![]()
![]()
![]()
Посчитаем все остальные показатели по вариационному ряду.
- дисперсия: ![]()
- относительный размах вариации: ![]()
- относительное линейное отклонение: ![]()
- коэффициент вариации: ![]()
Также необходимо узнать распределение показателя по всему диапазону значений. Для этого вычислим показатели характера вариации:
- коэффициент асимметрии: ![]()
- показатель эксцесса: ![]()
Для удобства и наглядности все полученные значения в ходе вычислений сведем в таблицу 2.3
Таблица 2.3 – Показатели вариации для распределения площади жилищ, приходящейся на одного жителя
| № п/п | Название показателя | Значение показателя |
| 1 | Среднее значение, кв.м/чел | 20,62 |
| 2 | Мода, кв.м/чел | 19,15 |
| 3 | Медиана, кв.м/чел | 21,19 |
| 4 | Размах вариации, кв.м/чел | 15,8 |
| 5 | Среднее линейное отклонение, кв.м/чел | 1,87 |
| 6 | Среднее квадратическое отклонение, кв.м/чел | 2,28 |
| 7 | Дисперсия, (кв.м/чел)2 | 5,20 |
| 8 | Относительный размах вариации | 0,77 |
| 9 | Относительное линейное отклонение, % | 0,09 |
| 10 | Коэффициент вариации, % | 0,11 |
| 11 | Коэффициент асимметрии | 1,55 |
| 12 | Эксцесс | - 0,15 |
Так как выполняется неравенство ![]() , то распределение не симметричное. Коэффициент асимметрии показывает, что существует значительная асимметрия.
, то распределение не симметричное. Коэффициент асимметрии показывает, что существует значительная асимметрия.
Отрицательный показатель эксцесса показывает, что разброс показателя достаточно велик. Цель вариационного анализа достигнута.
Похожие работы
... нормального распределения равны нулю: и . Вероятность попадания нормально распределенной случайной величины Х в заданный интервал (х1; х2) определяется по формуле (1): , (13) где Ф(х) – функция Лапласа, . (14) 4. Статистический анализ выборочной совокупности Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов. Объемом n выборочной ...
... 2272 9862 МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Санкт-Петербургский государственный университет аэрокосмического приборостроения СТАТИСТИКА Выборочные наблюдения Методические указания к практическим занятиям Санкт-Петербург 1999 Составитель Н.А. Богородская Рецензент кандидат экономических наук доцент Л.Г.Фетисова Методические ...
... данных и по внедрению накопленного арсенала современных методов прикладной статистики. По нашему мнению, широкого внедрения заслуживают, в частности, методы многомерного статистического анализа, планирования эксперимента, статистики объектов нечисловой природы. Очевидно, рассматриваемые работы должны быть плановыми, организационно оформленными, проводиться мощными самостоятельными организациями и ...
... вида выборочного наблюдения; 6) установление сроков проведения наблюдения; 7) определение потребности в кадрах для проведения выборочного наблюдения, их подготовка; 8) оценка точности и достоверности данных выборки, определение порядка их распространения на генеральную совокупность. Представление о статистических данных, как о выборочных, может относиться не только к собственно выборке, но и ...
0 комментариев