Расширение системы без использования франчайзинга

1.  Расширение системы без использования франчайзинга.

На начальной стадии развития компания не может создать эффективную франчайзинговую сеть из-за своей малой известности. Пусть P_c^f — доля территории рынка, охваченная предприятиями компании – потенциального франчайзера, обеспечивающая ему достаточную известность и репутацию для начала продажи франшиз (P_c^f < 1). Тогда условиями нахождения компании на первом этапе будут:

P_C(t) £ P_c^f, P_Ф(t) = 0.

2.  Экстенсивное развитие с применением франчайзинга.

Так как для данной работы представляет интерес только случай, когда компании выгодно создавать франчайзинговые точки (  ), то после получения возможности продажи франшиз фирма попытается максимально увеличить количество франчайзинговых предприятий, в том числе продавая во франчайзинг свои точки. Но при снижении доли собственных предприятий в сети ниже определенного уровня (P_Ф > nP_C, n > 0) потенциальные франчайзи могут утратить доверие к этой системе, сделав из такого снижения вывод о невыгодности занятия этим бизнесом.

Поэтому этап экстенсивного развития системы с использованием франчайзинга следует разбить на два подэтапа:

2.1. Увеличение доли франчайзинговых предприятий в системе. Условия нахождения системы на этом подэтапе:

P_Ф(t) < nP_C(t), P_c^f £ P_C(t) + P_Ф(t) < 1.

Обозначим через S — темп, с которым франчайзер может продавать свои собственные предприятия во франчайзинг, то есть .

2.2. Сбалансированный рост. В этой стадии развития системы франчайзер расширяет сеть предприятий, поддерживая максимально возможную долю франчайзинговых предприятий в системе, то есть в этом случае

P_Ф(t) = nP_C(t), P_C(t) + P_Ф(t) < 1.

3.  Функционирование на полностью охваченном сетью предприятий данной системы рынке.

В рамках рассматриваемой модели при полностью охваченном рынке (P_c(t) + P_ф(t) = 1) франчайзер может увеличить прибыль, только выкупая франчайзинговые предприятия или погашая свою задолженность. Хотя на практике франчайзеру выгоднее может быть поиск новых рынков или других сфер деятельности, а также исследования по улучшению производимого товара, повышение затрат на рекламу или совершенствование организационной структуры системы, а соотношение франчайзинговых и собственных предприятий сохранять далее почти неизменным.

Пусть dL — вариация размера задолженности франчайзера, тогда при сохранении полного охвата рынка из (16) и (18) – (20) для вариации доли собственных точек dP_C получим:

adL = (Z – E) dP_C ,

тогда из (17) вариация прибыли

dY = [p_c + rp_ф – r₁(Z – E)/a] dP_C .

Поэтому в рамках модели при ставке по кредиту

r₁ > a(p_c + rp_ф)/(Z – E)

франчайзеру выгодно сначала погашать из прибыли задолженность, а затем уже выкупать франчайзинговые предприятия, а при меньших ставках ему лучше поступить наоборот.

Далее система функционирует в стационарном режиме.

На каждом из рассмотренных этапов задача сводится к решению обыкновенных дифференциальных уравнений, их которых с использованием начальных данных определяются динамика задолженности, доли франчайзинговых и собственных предприятий, прибыль франчайзера и время нахождения системы на данном этапе.

Предложенной модели можно придать несколько иную форму, которая во многих случаях лучше описывает реальную ситуацию.

Сравнивая эффективность организации разных типов предприятий на конкретной территории, можно разбить рынок на две части так, что на одной из них франчайзеру выгодно продавать франшизы, а на другой — создавать собственные предприятия. Тогда можно использовать те же соотношения, считая, что p_ф — доход франчайзинговой единицы на первой части рынка, а p_с — прибыль от собственной единицы на второй. При этом необходимо учитывать размеры франчайзинговой (P_ф^L) и собственной (P_c^L) частей.

При такой трактовке очевидно, что на подэтапе 2.1 (увеличение доли франчайзинговых точек в системе) собственные точки не будут продаваться во франчайзинг, то есть S = 0.

Расширение сети по рассмотренному выше сценарию продолжится до тех пор, пока не будет полностью охвачена одна из частей рынка, иными словами либо P_ф(t) = P_ф^L, либо P_с(t) = P_с^L.

В первом случае оставшаяся часть заполняется собственными предприятиями, следовательно, задача (28) – (31) решается при условии P_ф(t) º P_ф^L.

Во втором случае нельзя по аналогии заполнить оставшаюся часть только франчайзинговыми точками, так как нарушится условие доверия потенциальных франчайзи к системе (доля франчайзинговых предприятий должна удовлетворять условию P_Ф(t) £ nP_C(t) ). Поэтому на неохваченном участке необходимо осуществлять сбалансированное расширение, то есть решать задачу (28) – (31) при условии P_Ф(t) = nP_C(t) и с другими коэффициентами прибыли p_с¹ и затрат E¹ на создание собственных предприятий франчайзера в этом секторе рынка.

Несмотря на существенную упрощенность, модель позволяет найти важные ориентиры для развития франчайзинговой сети.

МИНИМИЗАЦИЯ РИСКА

 

Франчайзер может руководствоваться, вырабатывая свою стратегию, принципом минимизации риска при определенном уровне средней ожидаемой прибыли.

Предположим, что цены внутри рассматриваемой системы различаются слабо и рынок можно разбить на n территориальных сегментов так, что во всех частях одного и того же сегмента динамика спроса одинакова, а собственные и франчайзинговые предприятия сети могут охватить при достаточных средствах любую часть рынка.

Пусть D — случайная величина, равная совокупному спросу на реализуемый рассматриваемой системой товар. Предположим, что спрос в i-ом сегменте можно, взяв совокупный спрос в качестве ведущего фактора, представить в виде:

D_i = a_i + b_iD + e_i,

где e_i — "собственные" некоррелированные случайности с нулевым математическим ожиданием, то есть M{(D-M{d}) e_i} = 0, M{e_i} = 0 и M{e_ie_j} = 0 при i ¹ j, а коэффициенты a_i и b_i определяются методом наименьших квадратов при анализе данных по предшествующим периодам времени. Поэтому для применения рассматриваемого метода необходимо наличие статистических данных о спросе на каждом из сегментов рынка за достаточно длительный промежуток времени.

Будем использовать для описания системы векторы размерностью 2n, обозначая первыми n компонентами характеристики франчайзинговых предприятий, а остальными — собственных предприятий в соответствующих секторах.

Если франчайзинговые предприятия системы охватывают весь сегмент, то прибыль франчайзера от этого сегмента составит

p_i = rD_i,

а ее математическое ожидание

p_i = M{p_i} = r(a_i + b_id),

где d = M{D}. Будем считать, что имеется большой объем данных по совокупному спросу за предшествующие периоды, поэтому можно определять d как среднее от этих величин.

Полагая переменные затраты пропорциональными объему реализации (c — коэффициент пропорциональности), получаем, что при охвате собственными предприятиями франчайзера всего сегмента, его прибыль от этого сегмента:

p_n+j = (1 – c)D_j – S_j,

где S_j — постоянные затраты. Тогда математическое ожидание прибыли:

p_n+j = M{p_n+j} = (1 – c)(a_j + b_jd) – S_j.

Пусть s² = M{(D – d)²} — дисперсия совокупного спроса, которую, также как и M{e_i²}, будет считать, усредняя данные по предшествующим периодам. Тогда ковариационная матрица V возможных прибылей определяется следующим образом:

если iÎ[1, n] и jÎ[1, n], то

V_ij = r²b_ib_js² при i ¹ j, V_ii = r² (b_i²s²+M{e_i²}),

если iÎ[1, n] и jÎ[n+1, 2n], то

V_i,j-n = r (1 – c) b_ib_j-n s², а V_i,i+n = r (1 – c) (b_i²s²+ M{e_i²}),

если iÎ[n+1, 2n] и jÎ[n+1, 2n], то

V_ij = (1 – c)²b_ib_js² при i ¹ j, V_ii = (1 – c)² (b_i²s²+M{e_i²}).

Остальные элементы определяются из условия V_ij = V_ji.

Пусть x_i и x_n+i — доли i-ого сектора, обслуживаемые франчайзинговыми и собственными предприятиями соответственно. Очевидно, что

(1) x ³ 0 ,

x_i + x_n+i £ 1.

Если определить матрицу S = {E, E}, где E — единичная матрица размера nxn, то последнее неравенство примет вид:

(2) Sx £ I ,

 

где I — вектор размерности n, состоящий из единиц.

Обозначим через N_i и N_n+i затраты на создание соответстенно франчайзинговых и собственных предприятий, охватывающих весь i-ый сегмент рынка. Если K — размер инвестиций франчайзера в развитие сети, то

(3) N^tx = K .

Пусть p — определенный франчайзером уровень средней ожидаемой прибыли. Тогда

(4) p^Tx = p.

В качестве меры риска удобно взять вариацию прибыли x^TVx.

Обозначив M^T = {N, p}, h = {K, p}, задача минимизации риска при ограничениях (1) – (4) примет вид

(5) min {x^TVx | Mx = h, x ³ 0, Sx £ I}

Функция Лагранжа рассматриваемой задачи:

L(x, l, m, n) = x^TVx + l^T(Mx – h) – m^Tx + n^T(Sx – I),

где l, m ³ 0, n ³ 0 — множители Лагранжа.

Из условия экстремума = 2Vx + l^TM^T – m + n^TS^T = 0 получим:

x = ½ V^-1(m – l^TM^T – n^TS^T).

Подставляя это выражение в условие Mx = h и выражая оттуда l, имеем:

l = (MV^-1M^T)^-1[MV^-1(m – n^TS^T) – 2h],

поэтому с учетом условий дополняющей нежесткости оптимальное распределение собственных и франчайзинговых предприятий системы x* находится из системы (6) – (7):

(6) x* = ½ V^-1{M^T (MV^-1M^T)^-1 [2h – MV^-1(m – n^TS^T)] + m – n^TS^T},

(7) m_i x*_i = 0, n_i (x*_i + x*_n+i – 1) = 0, m_i ³ 0, n_i ³ 0, x^*_i ³ 0, x*_i + x*_n+i £ 1.

Оценим теперь вероятность убыточной работы франчайзи и франчайзера. Если переменные затраты франчайзи, работающих на i-ом сегменте рынка, пропорциональны объему реализации, то есть равны c_aD_ix_i, то их деятельность будет убыточной при условии (1 - r)D_i < c_aD_i + W_i , где W_i — постоянные затраты франчайзи в случае охвата ими всего i-ого сегмента. Значит, критическая величина спроса D_кр,i = W_i / (1 – r – c_a).

Из гипотезы D_i = a_i + b_iD + e_i следует, что средний ожидаемый спрос на i-ом сегменте рынка d_i = M{D_i} = a_i + b_id, а его дисперсия s_i² = b_i²s² + M{e_i²}. Тогда, считая, естественно, что d_i > D_кр,i, с помощью неравенства Чебышева P{|D_i – d_i| > d} < s_i² / d можно оценить вероятность убыточной работы франчайзи на i-ом сегменте рынка:

.

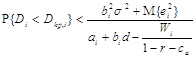Так как “собственные” случайности e_i некоррелированы, то предположим, что в целом по всем сегментам рынка они практически компенсируют друг друга. Тогда условием убыточной деятельности франчайзера будет следующее неравенство:

.

Следовательно, критическая величина совокупного спроса

.

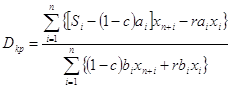Отсюда с помощью неравенства Чебышева получаем оценку вероятности убыточной работы франчайзера:

P{D < D_кр} < s² / (d – D_кр),

при этом, естественно, предполагается, что d > D_кр.

Так как франчайзер регулярно получает от франчайзи и своих управляющих данные по реализации товаров, то он, зная их доли на соответствующих сегментах рынка, может вычислить спрос в отчетном периоде на каждом сегменте. После такой обработки поступивших данных франчайзеру следует заново пересчитать по методу наименьших квадратов коэффициенты a_i и b_i и средний совокупный спрос d. Далее он может с помощью скорректированных значений дать прогноз спроса на каждом секторе рынка по формуле d_i = a_i + b_id, откуда сразу вычисляется и предполагаемое значение спроса для каждого франчайзи и собственных предприятий.

В качестве предполагаемого значения совокупного спроса лучше брать не его среднюю величину по предыдущим периодам, а прогнозную, получаемую франчайзером с помощью технического анализа динамики спроса и с учетом различных факторов, влияющих на него.

В целях более обоснованного планирования деятельности элементов системы прогноз по каждому предприятию сети имеет смысл направлять соответствующему управляющему или франчайзи, так как они обычно не имеют возможности провести столь серьезный анализ, хотя зачастую могут внести в него собственные коррективы, опираясь на информацию регионального уровня.

ЗАКЛЮЧЕНИЕ

Тенденции развития мировой экономики указывают на дальнейшее увеличение использования франчайзинга как эффективной и гибкой формы организации бизнеса, позволяющей снизить риск в малом предпринимательстве и способствующей быстрому продвижению современных технологий как в производственной сфере, так и в сфере услуг. При этом повышается мотивация на нижнем уровне управления.

В России до сих пор франчайзинг применяется крайне редко, хотя потенциальные возможности его использования здесь очень велики.

Наиболее перспективной представляется организация иностранными компаниями, обладающими передовыми технологиями и известной торговой маркой, дилерских или торгово-производственных франчайзинговых сетей для быстрого проникновения на российский рынок. При этом риск и затраты иностранных инвесторов практически минимальны. Нынешнее, явно недостаточное их участие в российской экономике, а, следовательно, и перспектива увеличения притока зарубежных инвестиций позволяют прогнозировать бурный рост франчайзинговых систем в России уже в ближайшее время.

Хотя пока немногие российские компании обладают устоявшейся репутацией и широко известной торговой маркой, некоторые из них могут создавать собственные франчайзинговые сети уже сейчас. Наиболее очевидными видятся возможности использования франчайзинга отечественными нефтяными компаниями для организации системы бензоколонок и автомобильными заводами для торговли и обслуживания производимых ими машин. Часть этих франчайзинговых точек может располагаться и за границей, особенно, в странах СНГ и в Прибалтике.

ЛИТЕРАТУРА

1.   New Developments in Franchising. Washington: Gov. print. off., 1992

2.   Hoffman R., Preble J. Franchising: Selecting a Strategy for Rapid Growth // Long Range Planning, 1991, V.24, ¹4, 74-85

3.   Stigliz J.E. Incentives and Risk-Sharing in Sharecropping // Review of Economic Studies, 1974, V.41, 219-255

4.   Martin R.E. Franchising and Risk Management // American Economic Review, 1988, V.78, ¹5, 954-968

5.   Mathewson G., Winter R.. The Economics of Franchise Contracts // Journal of Law and Economics, 1985, V.28, ¹3, 503-526

6.   Rubin P. The Theory of the Firm and the Structure of Franchise Contract // Journal of Law and Economics, 1978, V.21, ¹1, 223-233

7.   Lal R. Improving Channel Coordination through Franchising // Marketing Science, 1990, V.9, 299-318

8.   Caves R.E., Murphy W.F. Francising: Firms, Markets and Intangible Assets // Southern Economic Journal, 1976, V.42, 572-586

9.   Tirole J. The Theory of Industrial Organization. Cambridge (Mass): MIT Press, 1988

10.   Lafontaine F. Agency Theory and Franchising: Some Empirical Results // RAND Journal of Economics, 1992, V.23, ¹2, 263-283