Навигация
Аналитическое выравнивание проведем по методу скользящей средней. Находим средние значения признака для каждой тройки соседних лет
2.6. Аналитическое выравнивание проведем по методу скользящей средней. Находим средние значения признака для каждой тройки соседних лет.
| Годы | Выпуск продукции, тыс.усл.ед. | Средние значения для тройки соседних лет |
| 1 | 1476 | |
| 2 | 1529 | |
| 3 | 1607 | 1537,3 |
| 4 | 1598 | 1578 |
| 5 | 1673 | 1626 |
| 6 | 1702 | 1657,7 |
| 7 | 1680 | 1685 |
| 8 | 1658 | 1680 |
| 9 | 1612 | 1650 |
| 10 | 1639 | 1636,3 |
Выровненные значения показываем на графике.
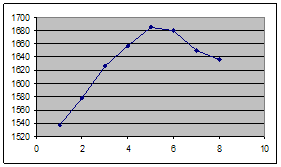
Вывод. При использовании метода аналитического выравнивания динамического ряда и отображения результатов графически прослеживается тенденция увеличения выпуска продукции первые 5 лет и дальнейшее снижение выпуска продукции. Эти результаты подтверждаются расчетом частных средних абсолютных приростов и темпов роста.
2.8. Проанализируем сезонные колебания объема выпуска продукции за три года. Построим динамическую таблицу, содержащую объем выпуска продукции за три года. Таблица В Динамика помесячного выпуска продукции| Месяц | Год | ||
| первый | второй | третий | |
| 1 | 287 | 295 | 302 |
| 2 | 262 | 280 | 292 |
| 3 | 284 | 298 | 314 |
| 4 | 335 | 350 | 327 |
| 5 | 354 | 363 | 329 |
| 6 | 362 | 384 | 392 |
| 7 | 380 | 392 | 397 |
| 8 | 387 | 398 | 403 |
| 9 | 330 | 358 | 411 |
| 10 | 321 | 319 | 403 |
| 11 | 301 | 307 | 364 |
| 12 | 274 | 265 | 315 |
Рассчитаем индексы сезонности по формуле:
 ,
,
где, ![]() - средняя за месяц,
- средняя за месяц, ![]() - средняя за год.
- средняя за год.
Определим осредненные значения уровней для каждого месяца годового цикла, среднюю за год, индексы сезонности.
| Месяц | Осредненное значение уровня | Индексы сезонности | ||
| расчет | итого | 0,860116 | ||
| 1 | (287+295+302)/(31+31+31) | 9,505 | 0,86743 | |
| 2 | (262+280+292)/(29+29+29) | 9,586 | 0,871792 | |
| 3 | (284+298+314 )/(31+31+31) | 9,634 | 1,01748 | |
| 4 | (335+350+327)/(30+30+30) | 11,244 | 1,017739 | |
| 5 | (354+363+329)/(31+31+31) | 11,247 | 1,144162 | |
| 6 | (362+384+392)/(30+30+30) | 12,644 | 1,137416 | |
| 7 | (380+392+397)/(31+31+31) | 12,570 | 1,155903 | |
| 8 | (387+398+403)/(31+31+31) | 12,774 | 1,104951 | |
| 9 | (330+358+411)/(30+30+30) | 12,211 | 1,01482 | |
| 10 | (321+319+403)/(31+31+31) | 11,215 | 0,977263 | |
| 11 | (301+307+364)/(30+30+30) | 10,800 | 0,830927 | |
| 12 | (274+265+315)/(31+31+31) | 9,183 | 0,860116 | |
| Сумма |
| |||
![]()
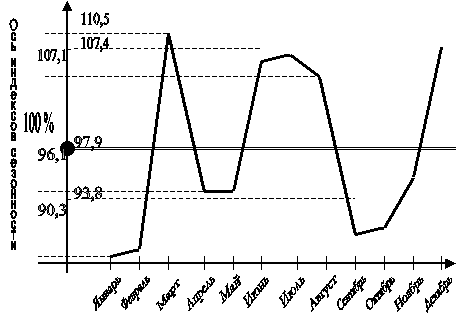
На графике изобразим сезонную волну:
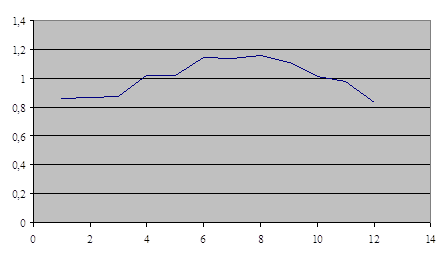
3.1. Рассчитать индивидуальные индексы цен и физического объема.
3.2. Рассчитать общий индекс цен в агрегатной форме по методикам Пааше, Ласпейреса.
3.3. Рассчитать общий индекс физического объема в агрегатной форме.
3.4. Рассчитать общий индекс стоимости. Показать взаимосвязь индексов цены, физического объема и стоимости.
3.5. Рассчитать влияние факторов на изменение общей стоимости товаров.
3.6. Показать методику преобразования общих индексов цен (Пааше, Ласпейреса) и общего индекса физического объема в средние индексы. Рассчитать общие индексы цен методом среднего индекса.
Решение
Исходные данные:
Цены и физический объем реализованной продукции (цена в рублях, физический объем в тысячах условных единицах)
| Товар-представитель | ||||||||
| А | Б | В | Г | |||||
| цена | физ. объем | цена | физ. объем | цена | физ. объем | цена | физ. объем | |
| Базовый период | 13,2 | 400 | 3,8 | 2540 | 25,7 | 184 | 83,5 | 156 |
| Текущий период | 11,2 | 403 | 3,1 | 2564 | 29,5 | 194 | 80,9 | 175 |
3.1. Индивидуальные индексы находим по формулам:
![]() -индивидуальный индекс цен,
-индивидуальный индекс цен,
![]() -индивидуальный индекс физического объема продаж.
-индивидуальный индекс физического объема продаж.
Результаты вычислений представляем в таблице:
| Товар- представитель | Базовый период | Текущий период | Индиви-дуальный индекс цен | Индивидуальный индекс физического объема продаж
| ||
| цена.
| объем
| цена
| объем
| |||
| А | 13,2 | 400 | 11,2 | 403 | 0,848 | 1,008 |
| Б | 3,8 | 2540 | 3,1 | 2564 | 0,816 | 1,009 |
| В | 25,7 | 184 | 29,5 | 194 | 1,148 | 1,054 |
| Г | 83,5 | 156 | 80,9 | 175 | 0,969 | 1,122 |
3.2. Рассчитаем общий индекс цен в агрегатной форме по методикам Пааше, Ласпейреса.
| Товар- предс-тавитель | Базовый период | Текущий период | Стоимость продукции | |||||
| в текущих ценах | текущего периода в сопоста-вимых ценах | базового периода в текущих ценах | ||||||
| цена, руб. | объем, тыс. ед. | цена, руб. | объем, тыс. ед. | 2003 года | 2004 года | |||
| Символ |
|
|
|
|
|
|
|
|
| А | 13,2 | 400 | 403 | 11,2 | 5280 | 4513,6 | 5319,6 | 4480 |
| Б | 3,8 | 2540 | 2564 | 3,1 | 9652 | 7948,4 | 9743,2 | 7874 |
| В | 25,7 | 184 | 194 | 29,5 | 4728,8 | 5723 | 4985,8 | 5428 |
| Г | 83,5 | 156 | 175 | 80,9 | 13026 | 14157,5 | 14612,5 | 12620,4 |
| Сумма | 3280 | 3336 | 32686,8 | 32342,5 | 34661,1 | 30402,4 | ||
Общий индекс цен Пааше:
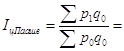 30402,4/ 32686,8=0,93 (93%).
30402,4/ 32686,8=0,93 (93%).
Цены снизились на 7%. Общий индекс цен Ласпейреса:
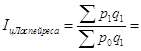 32342,5/ 34661,1=0,933 (93,3%).
32342,5/ 34661,1=0,933 (93,3%).
Цены снизились на 6,7%.
3.3. Общий индекс физического объема в агрегатной форме:
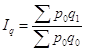 = 34661,1/ 32686,8= 1,06 (106%).
= 34661,1/ 32686,8= 1,06 (106%).
Физический объем увеличился на 6%.
3.4. Общий индекс стоимости:
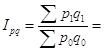 32342,5/ 32686,8 =0,989 (98,9%).
32342,5/ 32686,8 =0,989 (98,9%).
Стоимость уменьшилась на 1,1%. Взаимосвязь индексов:![]()
3.5. Рассчитаем влияние факторов на изменение общей стоимости товаров. Абсолютная сумма изменения общей стоимости товаров:
![]() 32342,5 – 32686,8 = -344,3
32342,5 – 32686,8 = -344,3
- общая стоимость товаров уменьшилась на 344,3 руб.
Абсолютная сумма изменения общей стоимости товаров за счет изменения цен:
![]() 32342,5 - 34661,1 = -2318,6
32342,5 - 34661,1 = -2318,6
- за счет изменения цен общая стоимость товаров уменьшилась на 2318,6 руб.
Абсолютная сумма изменения общей стоимости товаров за счет изменения количества товаров:
![]() 34661,1- 32686,8 = 1974,3
34661,1- 32686,8 = 1974,3
- за счет изменения количества товаров стоимость товаров увеличилась на 1974,3 руб.
3.6. Методик преобразования общих индексов в средние.
Общий индекс цен Пааше:
 .
.
Общий индекс цен Ласпейреса:
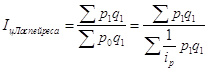 .
.
Общий индекс физического объема:
 .
.
Рассчитать предельную ошибку выборки для средней и для доли с вероятностью, указанной для варианта и границы, в которые попадает генеральная средняя или генеральная доля.
Решение
Исходные данные:
Генеральная численность единиц совокупности N = 48400.
Выборочная численность единиц совокупности п = 200.
Средняя ![]() =11,26.
=11,26.
Среднее квадратическое отклонение ![]() =3,27
=3,27
Выборочная доля W = 0,042.
Вероятность, с которой гарантируется результат F(t) = 0,997.
Среднюю ошибку выборки для средней вычисляем по формуле:
![]() .
.
Среднюю ошибку выборки для доли вычисляем по формуле
 .
.
Так как вероятность, с которой гарантируется результат равна 0,997, то уровень коэффициента доверия ![]() .
.
Получаем среднюю ошибку выборки для средней: ![]()
Получаем среднюю ошибку выборки для доли:
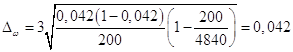
Предельную ошибку выборки вычисляем по формуле:
![]() .
.
Получаем предельную ошибку выборки для средней:
![]()
Границы, в которые попадает генеральная средняя вычисляем по формуле: ![]() Получаем
Получаем ![]() ,
, ![]()
Генеральная средняя с вероятностью 0,997 находится в интервале от 10,58 до 11,94.
Границы, в которые попадает генеральная генеральная доля вычисляем по формуле:. ![]() . Получаем:
. Получаем: ![]() .
.
Доля единиц, обладающих определенным свойством с вероятностью 0,997 находится в интервале от 0 до 0,082.
Список литературы
1. Боярский А.Я., Громыко Г.Л. "Общая теория статистики" М.: изд. Московские университеты, 1985 г.
2. Гришин А.Ф. Статистика: Учеб. Пособие. – М.: Финансы и статистика, 2003. – 240с
3. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник.-М.:ИНФРА – М., 1996.- 416 с.
4. Ефремова М.Р. "Общая теория статистики"; М.: "Инфра-М", 1996
5. Кильдишев и др. "Общая теория статистики" М.: Финансы и Статистика, 1994 г
6. Переяслова И.Г., Колбачев Е.Б., Переяслова О.Г.Статистика. Серия "Высшее образование". – Ростов н/Д: "Феникс", 2003.- 288 с.
7. Сборник задач по теории статистики: Учебное пособие/Под ред. проф. В.В.Глинского и к.э.н. Л.К.Серга. – М.: ИНФРА-М; 2002.-257 с.
8. Статистика: Учебное пособие/Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; под ред. В.Г.Ионина. – Изд.2-е, перераб. и доп. – М.: ИНФРА-М, 2001.
9. Статистический словарь (под. ред. Ю.А.Юркова) М.: Финстатинформ, 1996
10. Экономическая статистика (под. ред. Ю.Н. Иванова) М.:ИНФРА-М, 1998 Кильдишев и др. "Общая теория статистики" М.: Финансы и Статистика, 1994 г
Похожие работы
... соответственно; q1, q2 - объем отчетного, базисного периодов соответственно) для величины (цены) по каждому виду товара для величины q (объема) по каждому виду товаров: Найдем общие индексы по формулам: представляет собой среднее значение индивидуальных индексов (цены, объема), где j – номер товара. Общий индекс товарооборота равен: Найдем абсолютное ...
... экономико-рыночных отношений в нашей стране ставит перед школой новые задачи. Умение анализировать, сравнивать различные ситуации необходимо на сегодняшний день каждому современному человеку. Элективный курс «Общая теория статистики» с помощью математического аппарата даст начальные понятия о статистике, которые необходимы при решении управленческих задач. Курс рассчитан для учащихся 11 класса ...
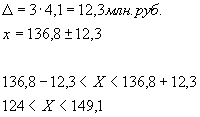
0 комментариев