Навигация
Принципи розв’язання статистичних задач
34952
знака
11
таблиц
1
изображение
1.3 Принципи розв’язання статистичних задач
Розглянемо гру з природою: у нас (сторона А) є т можливих стратегій 
; що стосується обстановки, то про неї можна зробити п припущень: 
. Розглянемо їх як «стратегії природи». Наш виграш 
при кожній парі стратегій 
заданий матрицею (таблиця 1.3.1).[2, c. 196-199]
Таблиця 1.3.1
|
|
|
|
|
| ||||
|
|
|
|
|
|
Необхідно вибрати таку стратегію гравця А (чисту, або можливо, змішану, якщо це можливо), яка є більш вигідною в порівнянні з іншими.
Найпростіший випадок вибору розв’язку в грі з природою — це випадок коли якась із стратегій гравця А перевершує інші («домінує» над ними), як, наприклад, стратегія А2 в таблиці 1.3.2.
Тут виграш при стратегії А2 при будь-якому стані природи не менше ніж при інших стратегіях, а при деяких — більше; значить потрібний вибирати саме цю стратегію.
Таблиця 1.3.2
 |
|
|
|
| ||||
|
|
|
|
|
|
Якщо навіть в матриці гри з природою немає однієї домінуючій над всіма іншими стратегії, все ж таки корисно подивитися, чи немає в ній дублюючих стратегій і поступливих іншим за всіх умов. Але тут є одна тонкість: так ми можна зменшити тільки число стратегій гравця А, але не гравця П. Припустимо, що «чищення» матриці проведено, і ні дублюючих, ні явно невигідних гравцю А стратегій в ній немає. Припустимо, що виграш 
при нашій стратегії Aiі стані природа 
більше, ніж при нашій стратегії Ak і стані природи 
: 
>
. Але за рахунок чого більше? За рахунок того, що вдало вибрали стратегію Ai? Необов'язково. Можливо, просто стан природи вигідніше, ніж . Наприклад, стан природи «нормальні умови» для будь-якої операції вигідніше, ніж «повінь», «землетрус» і т.п. Бажано ввести такі показники, які не просто давали б виграш при даній стратегії в кожній ситуації, але відображали б «вдачність» або «невдачність» вибору даної стратегії в даній ситуації. З цією метою в теорії рішень вводиться поняття «ризику». Ризиком 
гравця А при користуванні стратегією Ai в умовах називається різниця між виграшем, який ми отримали б, якби знали умови , і виграшем, який ми отримаємо, не знаючи їх і вибираючи стратегію Ai :
Для прикладу візьмемо матрицю виграшів ()(таблиця 1.3.3) і побудуємо для неї матрицю ризиків (
) (таблиця 1.3.4). При погляді на матрицю ризиків (таблиця 1.3.4) стають яснішими деякі риси даної «гри з природою». Так, в матриці виграшів () (таблиця 1.3.3) в другому рядку перший і останній елементи були рівні один одному: 
.
Таблиця 1.3.3
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
| 4 | 8 | 6 | 9 |
Таблиця 1.3.4
|
|
|
|
|
|
|
|
|
|
|
|
Проте ці виграші зовсім не рівноцінні в значенні вдалого вибору стратегії: при стані природи 
могли виграти найбільше 4, і вибір стратегії А2 майже абсолютно добрий; а ось при стані 
могли б, вибравши стратегію А1 отримати на цілі 6 одиниць більше, тобто вибір стратегії А2дуже поганий. Ризик — це «платня за відсутність інформації»: в таблиці 1.3.4 r21 = 1, r24= 6. Природно, хотілося б мінімізувати ризик, супроводжуючий вибір розв’язку.
Найпростіший випадок невизначеності — це «доброякісна або стохастична невизначеність», коли стани природи мають якісь вірогідності і цю вірогідності 
нам відомі. Тоді вибираємо ту стратегію, для якої середнє значення виграшу, узяте по рядку, максимально:
А середній ризик повинен бути мінімальним:
Припустимо, що вірогідність у принципі існує, але невідомі. Іноді в цьому випадку припускають всі стани природи рівноімовірними (так званий «принцип недостатньої підстави» Лапласа), але взагалі-то це робити не рекомендується. Все-таки звичайно більш менш ясно, які стани більш, а які — менш вірогідні. Для того, щоб знайти орієнтовні значення вірогідностей , можна, наприклад, скористатися методом експертних оцінок.
Візьмемо випадок «поганої невизначеності», коли вірогідність станів природи або взагалі не існують, або не піддаються оцінці навіть приблизно. Тут все залежить від точки зору на ситуацію, від позиції дослідника, від того, якими бідами загрожує невдалий вибір рішення. Опишемо декілька можливих підходів, точок зору (або, як то кажуть, декілька «критеріїв» для вибору рішення).
1. Максимінний критерій Вальда. [2, c. 196] Згідно цьому критерію гра з природою ведеться як гра з розумним, причому агресивним супротивником, що робить все для того, щоб перешкодити нам досягти успіху. Оптимальною вважається стратегія, при якій гарантується виграш у будь-якому випадку не менший, ніж «нижня ціна гри з природою»:
.
Якщо керуватися цим критерієм, що втілює «позицію крайнього песимізму», треба завжди орієнтуватися на гірші умови, знаючи напевно, що «гірше цього не буде». Очевидно, такий підхід — «перестраховочный», природний для того, хто дуже боїться програти, — не є єдино можливим, але як крайній випадок він заслуговує розгляду.
Похожие работы
... методи екологічного виховання необхідно змінювати, чергувати залежно від змісту, мети вивчення теми, рівня підготовки учнів. 2.3 Виховання бережливого ставлення до природи у процесі гри У становленні емоційно-ціннісного, відповідального ставлення молодшого школяра до природи важливу роль відіграє гра. Найважливішим результатом гри є глибока емоційна задоволеність дитини її процесом, що найб ...
... значення має ігра для величезної кількості збиткових, нерозвинених дітей, яких необхідно виховувати сьогодні, оскільки завтра буде пізно. 5. Ігра одночасно - розвиваюча діяльність, принцип, метод і форма життєдіяльності, зона соціалізації, захищеності, самореабілітації, співпраці, співдружності, співтворчості з дорослими, посередник між світом дитини і світом дорослого. 6. Сучасна гуманістична ...
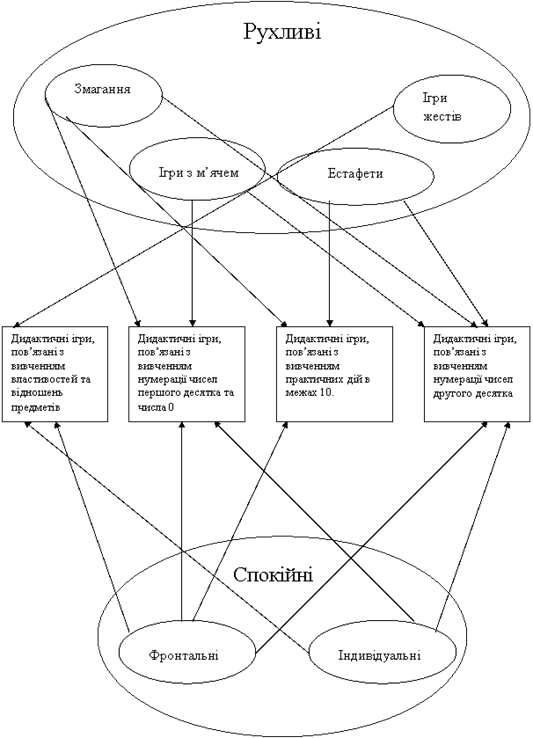
... учнів буде більш раціональною і продуктивною за умови оптимального застосування системи дидактичних ігор. Важливою умовою підвищення ефективності навчального процесу є використання розвивального потенціалу дидактичної гри у початковій школі, яка б допомагала здійснювати оптимальну навчально-пізнавальну діяльність молодших школярів. Проведений аналіз наукової літератури засвідчив, що проблема ...
... , і умова, що дають змогу повніше використовувати можливості учнів. Пізнавальна самостійність формується у різних навчальних ситуаціях: сприйнятті готового матеріалу, спрямованій пізнавальній активності, дослідницькій пізнавальній діяльності. Ігри створюють певний емоційний фон в учнівському колективі, але й потребують певного емоційного настрою. Одним з принципів навчання є позитивне емоційне ...
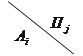
0 комментариев