Навигация
Критерій мінімаксного ризику Севіджа
2. Критерій мінімаксного ризику Севіджа.
Поняття ризику виявляється корисним і для введення інших принципів поведінки в іграх з природою. На ньому, зокрема, заснований критерій Севіджа, відповідно до якого в умовах невизначеності (вірогідність станів природи невідома) слід вибирати таку стратегію i0, яка гарантує мінімальний ризик, тобто
![]()
Цей критерій — теж украй песимістичний, але при виборі оптимальної стратегії радить орієнтуватися не на виграш, а на ризик. Сутність такого підходу в тому, щоб всіляко уникати великого ризику при ухваленні рішення. В значенні «песимізму» критерій Севіджа схожий з критерієм Вальда, але самий «песимізм» тут розуміється по-іншому.
Покажемо на прикладі, що критерій Севіджа, взагалі кажучи, відрізняється від критерію Вальда. Розглянемо матрицю:
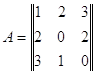
Для неї оптимальною по Вальду є перша стратегія:
![]() .
.
Відповідна матриці А матриця ризику є:
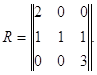
Оптимальною по Севіджу тут є друга стратегія: ![]() , тобто критерії Вальда і Севіджа в даному прикладі приводять до різних результатів (хоча можна навести і приклади, в яких виходять однакові результати).
, тобто критерії Вальда і Севіджа в даному прикладі приводять до різних результатів (хоча можна навести і приклади, в яких виходять однакові результати).
3. Критерій песимізму-оптимізму Гурвіца. Цей критерій рекомендує при виборі рішення не керуватися ні крайнім песимізмом, ні крайнім, легковажним оптимізмом. Згідно цьому критерію вибирається стратегія з умови
![]()
де ![]() — «коефіцієнт песимізму», вибраний між нулем і одиницею.
— «коефіцієнт песимізму», вибраний між нулем і одиницею.
При ![]() = 1 критерій Гурвіца перетворюється на критерій Вальда; при
= 1 критерій Гурвіца перетворюється на критерій Вальда; при ![]() = 0 — в критерій «крайнього оптимізму», що рекомендує вибрати ту стратегію, при якій найбільший виграш в рядку максимальний. При 0 <
= 0 — в критерій «крайнього оптимізму», що рекомендує вибрати ту стратегію, при якій найбільший виграш в рядку максимальний. При 0 <![]() < 1 виходить щось середнє між тим і іншим. Коефіцієнт
< 1 виходить щось середнє між тим і іншим. Коефіцієнт ![]() вибирається з суб'єктивних міркувань — чим небезпечно ситуація, чим більше ми хочемо в ній «підстрахуватися», чим менша наша схильність до ризику, тим ближче до одиниці вибирається
вибирається з суб'єктивних міркувань — чим небезпечно ситуація, чим більше ми хочемо в ній «підстрахуватися», чим менша наша схильність до ризику, тим ближче до одиниці вибирається ![]() .
.
При бажанні можна побудувати критерій, аналогічний Н, виходячи не з виграшу, а з ризику, але ми на цьому не зупинятимемося.
На перший погляд здається, що вибір критерію — суб'єктивний, вибір коефіцієнта ![]() — теж суб'єктивний, значить і рішення теж приймається суб'єктивно, тобто, грубо кажучи, довільно.
— теж суб'єктивний, значить і рішення теж приймається суб'єктивно, тобто, грубо кажучи, довільно.
В якійсь мірі це дійсно так — вибір рішення в умовах невизначеності завжди умовний, суб'єктивний. Та все ж в якійсь (обмеженої) мірі математичні методи корисні і тут. Перш за все, вони дозволяють привести гру з природою до матричної форми, що далеко не завжди буває просто, особливо коли стратегій багато (в наведених прикладах їх було дуже мало). Крім того, вони дозволяють замінити просту матрицю виграшів (або ризиків), послідовним чисельним аналізом ситуації з різних точок зору, вислухати рекомендації кожній з них і, нарешті, зупинитися на чомусь визначеному. Це аналогічно обговоренню питання з різних позицій, а в суперечці, як відомо, народжується істина. Отже не слід чекати від теорії рішень остаточних, незаперечних рекомендацій — єдине, чим вона може допомогти — це порадою.
Якщо рекомендації, витікаючі з різних критеріїв, співпадають — тим краще, значить, можна сміливо вибрати рішення, що рекомендується: воно швидше за все не «підведе». Якщо ж, як це часто буває, рекомендації суперечать один одному, то треба з'ясувати, наскільки до різних результатам вони приводять, уточнити свою точку зору і провести остаточний вибір. Не треба забувати що в будь-яких задачах в обгрунтовуванні розв’язків деяке свавілля неминуче — хоча б при побудові математичної моделі, виборі показника ефективності. Вся математика, вживана в дослідженні операцій, не відміняє цього свавілля, а дозволяє тільки «поставити його на своє місце».
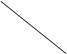
Розглянемо елементарний приклад «гри з природою» 4 ![]() 3, матриця виграшів якої (
3, матриця виграшів якої (![]() ) дана в таблиці 1.3.5.
) дана в таблиці 1.3.5.
Таблиця 1.3.5
 |
|
|
| ||||
|
|
|
|
|
Виберемо оптимальну стратегію користуючись критеріями Вальда, Севіджа і Гурвіца, причому в останньому візьмемо ![]() = 0,6 (перевага трохи у бік песимізму).
= 0,6 (перевага трохи у бік песимізму).
1. Застосуємо критерій Вальда. Підрахуємо мінімуми по рядках (див. таблицю 1.3.6) і виберемо ту стратегію, при якій мінімум рядка максимальний (рівний 25). Це — стратегія A3.
Таблиця 1.3.6
 |
|
|
|
| ||||
|
|
|
|
|
|
2. Застосуємо критерій Севіджа. Перейдемо від матриці виграшів (таблиця 1.3.6) до матриці ризиків (таблиця 1.3.7), в правому додатковому стовпці запишемо максимальне в рядку значення ризику ![]() .
.
З чисел правого стовпця мінімальне (60) відповідає стратегіям А2 і Аз; значить, обидва вони оптимальні по Севіджу.
Таблиця 1.3.7
 |
|
|
|
| ||||
|
|
|
|
|
|
3. Застосуємо критерій Гурвіца (при ![]() = 0,6). Знову перепишемо таблицю 1.3.5, але цього разу в правих трьох додаткових стовпцях поставимо: мінімум рядка
= 0,6). Знову перепишемо таблицю 1.3.5, але цього разу в правих трьох додаткових стовпцях поставимо: мінімум рядка ![]() , його максимум
, його максимум ![]() , і величину
, і величину ![]() , округлену до цілих одиниць (див. таблицю 1.3.8). Максимальне значення hi = 47 відповідає стратегії А3.
, округлену до цілих одиниць (див. таблицю 1.3.8). Максимальне значення hi = 47 відповідає стратегії А3.
Отже, в даному випадку всі три критерії однозначно говорять на користь стратегії А3, яку є всі підстави вибрати.
Таблиця 1.3.8
 |
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
Розглянемо випадок, коли між критеріями виникає «суперечка». Матриця виграшів (![]() ) (з наперед виписаними стовпцями мінімумів рядків
) (з наперед виписаними стовпцями мінімумів рядків ![]() , максимумами рядків
, максимумами рядків ![]() , і значеннями
, і значеннями ![]() (при
(при ![]() = 0,6)) дана в таблиці 1.3.9.
= 0,6)) дана в таблиці 1.3.9.
По критерію Вальда оптимальною є стратегія ![]() , по критерію Гурвіца з
, по критерію Гурвіца з ![]() = 0,6 — стратегія
= 0,6 — стратегія ![]() .
.
Таблиця 1.3.9
 |
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
По критерію Севіджа матриця ризиків з додатковим стовпцем, що містить максимуми рядків ![]() , дана в таблиці 1.3.10. Мінімальним в останньому стовпці є число 38, так що критерій Севіджа, так само як і критерій Гурвіца, показує стратегію
, дана в таблиці 1.3.10. Мінімальним в останньому стовпці є число 38, так що критерій Севіджа, так само як і критерій Гурвіца, показує стратегію ![]() .
.
Таблиця 1.3.10
 |
|
|
|
|
| ||||
|
|
|
|
|
|
|
Відзначимо наступне: всі три критерії (Вальда, Севіджа і Гурвіца) були сформульовано для чистих стратегій, але кожний з них може бути поширений і на змішані, подібно тому, як це робиться в теорії ігор. Проте змішані стратегії в грі з природою мають лише обмежене (головним чином, теоретичне) значення. Якщо в грі проти свідомого супротивника змішані стратегії іноді мають сенс як «трюк», що вводить в оману супротивника, то в грі проти «байдужої природи» цей резон відпадає. Крім того, змішані стратегії придбавають значення тільки при багатократному повторенні гри. А якщо вже її повторюємо, то неминуче починають вимальовуватися якісь риси вірогідності ситуації, і ми ними можемо скористатися для того, щоб застосувати «стохастичний підхід» до задачі, а він змішаних стратегій не дає.
Крім того, в ситуаціях з «поганою невизначеністю», коли болісно не вистачає інформації, головна задача — цю інформацію отримати, а не вигадувати хитромудрі методи, що дозволяють без неї обійтися. Одна з основних задач теорії статистичних рішень — це якраз планування експерименту, мета якого — з'ясування або уточнення якихось даних.
2. Практична частина Приклад 1
Уряд планує будівництво чотирьох типів електростанцій: ![]() (теплових),
(теплових), ![]() (пригребельних),
(пригребельних), ![]() (безшлюзових) і
(безшлюзових) і ![]() (шлюзових). Ефективність кожного з типів залежить від різних чинників: режиму річок, вартості палива і його перевезення і т.п. Необхідно вибрати самий оптимальний варіант.
(шлюзових). Ефективність кожного з типів залежить від різних чинників: режиму річок, вартості палива і його перевезення і т.п. Необхідно вибрати самий оптимальний варіант.
Розв‘язання
Припустимо, що виділено чотири різні стани, кожний з яких означає певне поєднання чинників, що впливають на ефективність енергетичних об'єктів. Стани природи позначимо через ![]() і
і ![]() . Економічна ефективність будівництва окремих типів електростанцій змінюється залежно від станів природи і задана матрицею:
. Економічна ефективність будівництва окремих типів електростанцій змінюється залежно від станів природи і задана матрицею:
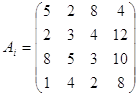
Згідно критерію Вальда:
![]()
![]()
![]()
![]()
Тоді оскільки ![]() , то слід передбачити будівництво безшлюзової ГЕС (А3).
, то слід передбачити будівництво безшлюзової ГЕС (А3).
Скористаємося критерієм Севіджа. Побудуємо матрицю ризиків:
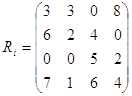
Покажемо як були отримані елементи матриці ризиків.
Оскільки ![]() , то:
, то:
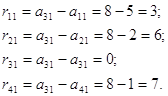
Поскольку ![]() , то:
, то:
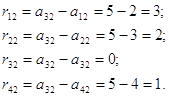
Поскольку ![]() , то:
, то:
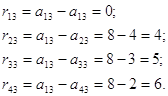
Поскольку ![]() , то:
, то:
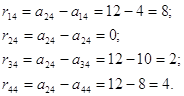
Згідно критерію Севіджа визначаємо ![]() . Відповідно до цього критерію також передбачається будівництво безшлюзової ГЕС (А3).
. Відповідно до цього критерію також передбачається будівництво безшлюзової ГЕС (А3).
Скористаємося критерієм Гурвіца. Припустимо ![]() ;
;
тоді:
![]()
![]()
![]()
![]()
![]()
Отримаємо ![]() , тобто слід прийняти рішення про будівництво пригребельних ГЭС(
, тобто слід прийняти рішення про будівництво пригребельних ГЭС(![]() ). Якщо ж припустити відомим розподіли вірогідності для різних станів природи, наприклад, якщо вважати ці стани рівноімовірними (
). Якщо ж припустити відомим розподіли вірогідності для різних станів природи, наприклад, якщо вважати ці стани рівноімовірними (![]() ), то для ухвалення рішення слід знайти математичне очікування виграшу:
), то для ухвалення рішення слід знайти математичне очікування виграшу:
![]()
![]()
![]()
![]()
Оскільки максимальне значення має М 3, то слід вибрати рішення А3.
Відповідно до даних отриманих в розв’язку можна зробити загальний висновок: використовуючи при розв’язку критерій Вальда і Севіджа була отримана рекомендація про будівництво безшлюзовой гідроелектростанції (А3), використовуючи при розв’язку критерій Гурвіца була отримана рекомендація про будівництво пригребельної гідроелектростанції(![]() ), але якщо ж припустити відомим розподіли вірогідності для різних станів природи, то дана рекомендація про будівництво безшлюзовой гідроелектростанції (А3) .
), але якщо ж припустити відомим розподіли вірогідності для різних станів природи, то дана рекомендація про будівництво безшлюзовой гідроелектростанції (А3) .
Приклад 2
Інвестор планує великі капіталовкладення в підприємство. Був проведений аналіз руху і технічного стану основних засобів. Дані приведені у таблиці 2.1.
| Підприємство | Коефіцієнт оновлення | Коефіцієнт придатності | Коефіцієнт приросту |
|
| 0,15 | 0,64 | 0,12 |
|
| 0,27 | 0,65 | 0,27 |
|
| 0,3 | 0,7 | 0,24 |
Таблиця 2.1 Дані про рух і технічний стан основних засобів
На основі цих даних інвестору необхідно зробити вибір.
Роз'вязання
Припустимо, що виділено три різні стани, кожний з яких означає певне поєднання чинників, що впливають на ефективність і прибутковість підприємства . Стани позначимо через ![]() . Складемо матрицю на основі отриманих даних :
. Складемо матрицю на основі отриманих даних :
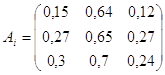
Згідно критерію Вальда:
![]()
![]()
![]()
Тоді оскільки ![]() , то слід на основі даних інвестувати в друге підприємство.
, то слід на основі даних інвестувати в друге підприємство.
Скористаємося критерієм Севіджа. Побудуємо матрицю ризиків:
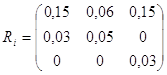
Покажемо як були отримані елементи матриці ризиків.
Оскільки ![]() , то:
, то:
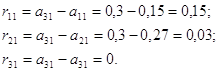
Поскольку ![]() , то:
, то:
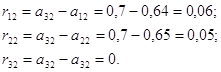
Поскольку ![]() , то:
, то:
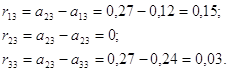
Згідно критерію Севіджа визначаємо
![]() .
.
Відповідно до цього критерію слід інвестувати у третє підприємство.
Скористаємося критерієм Гурвіца. Припустимо ![]() ;
;
тоді:
![]()
![]()
![]()
Отримаємо ![]() , тобто слід інвестувати у друге підприємство.
, тобто слід інвестувати у друге підприємство.
Відповідно до даних отриманих в розв’язку можна зробити загальний висновок: використовуючи при розв’язку критерій Вальда і Гурвіца була отримана рекомендація про інвестування у підприємство ![]() , використовуючи при розв’язку критерій Севіджа була отримана рекомендація про інвестування у підприємство
, використовуючи при розв’язку критерій Севіджа була отримана рекомендація про інвестування у підприємство ![]() .
.
Висновки
Специфічним видом ігор, що мають велике значення при аналізі різних практичних ситуацій, є статистичні ігри. Вони мають ряд істотних відмінностей від стратегічних ігор. В основі теорії стратегічних ігор лежить припущення, що інтереси двох гравців протилежні. Кожний з гравців прагне так вибрати свою стратегію, щоб отримати для себе найбільшу вигоду і звести до мінімуму вигоду супротивника. В таких іграх кожний гравець діє активно і прагне по можливості використовувати оптимальну стратегію. Під стратегією природи розуміється повна сукупність зовнішніх умов, в яких доводиться ухвалювати рішення. Цю сукупність зовнішніх умов називають станом природи ![]() . В загальному випадку існує деяка множина можливих станів природи
. В загальному випадку існує деяка множина можливих станів природи ![]() яка називатиметься простором стану природи, а елемент
яка називатиметься простором стану природи, а елемент ![]() цього простору – чистими стратегіями природи. Задача статистика полягає в тому, щоб ухвалити яке-небудь рішення або виконати яку-небудь дію з сукупності рішень або дій. Статистик повинен уміти оцінити кожну з своїх дій. Функція L(
цього простору – чистими стратегіями природи. Задача статистика полягає в тому, щоб ухвалити яке-небудь рішення або виконати яку-небудь дію з сукупності рішень або дій. Статистик повинен уміти оцінити кожну з своїх дій. Функція L(![]() , а) називається функцією втрат. Знання функції втрат дозволяє статистику зробити дії, які є якнайкращими в умовах інформації, яку він має про стан природи. Знання апріорного розподілу вірогідності дозволяє визначити середні втрати, які несе статистик, виконуючи ту або іншу дію. Статистична гра може бути представлена у вигляді еквівалентної S-гри абсолютно таким же чином, як це робилося в стратегічних іграх. Не існує універсального правила, що дозволяє вибрати, певний образ дії незалежно від ситуації, що склалася. Принципом вибору називають правило, що дозволяє визначити якнайкращу, змішану стратегію статистика. В різних випадках статистик може користуватися різними принципами вибору своєї стратегії. Одним з можливих принципів вибору стратегії може бути принцип мінімакса, який успішно застосовують в стратегічних іграх, коли гра ведеться проти розумного супротивника, охочого заподіяти нам найбільший збиток. Проте у ряді випадків доцільно використовувати цей принцип і в статистичних іграх. Мінімаксні принципи, витікаючі з припущення, що природа діє якнайгіршим для статистика чином, є виправданими в стратегічних іграх, але в статистичних іграх вони виражають точку зору дуже обережної людини, що прагне отримати доступне і що не ганяється за нездійсненним, щоб не потерпіти випадково великого збитку. Недоліком мінімаксних принципів слід рахувати також те, що вони не враховують апріорної інформації про стани природи і тим самим обмежують той виграш, який ця інформація може дати. Іншим принципом вибору стратегії, що враховує апріорний розподіл вірогідності, є байесовський принцип. Байесовський принцип, природно, можна застосовувати як до повних, так і до додаткових втрат. Найпростіший випадок вибору рішення в грі з природою — це випадок коли якась із стратегій гравця А перевершує інші («домінує» над ними). Тут виграш домінуючої стратегії при будь-якому стані природи не менше ніж при інших стратегіях, а при деяких — більше; значить потрібний вибирати саме цю стратегію. Якщо навіть в матриці гри з природою немає однієї домінуючої над всіма іншими стратегії, все ж таки корисно подивитися, чи немає в ній дублюючих стратегій і поступливих іншим за всіх умов. Згідно критерію Вальда гра з природою ведеться як гра з розумним, причому агресивним супротивником, що робить все для того, щоб перешкодити нам досягти успіху. Оптимальною вважається стратегія, при якій гарантується виграш у будь-якому випадку не менший, ніж «нижня ціна гри з природою».
, а) називається функцією втрат. Знання функції втрат дозволяє статистику зробити дії, які є якнайкращими в умовах інформації, яку він має про стан природи. Знання апріорного розподілу вірогідності дозволяє визначити середні втрати, які несе статистик, виконуючи ту або іншу дію. Статистична гра може бути представлена у вигляді еквівалентної S-гри абсолютно таким же чином, як це робилося в стратегічних іграх. Не існує універсального правила, що дозволяє вибрати, певний образ дії незалежно від ситуації, що склалася. Принципом вибору називають правило, що дозволяє визначити якнайкращу, змішану стратегію статистика. В різних випадках статистик може користуватися різними принципами вибору своєї стратегії. Одним з можливих принципів вибору стратегії може бути принцип мінімакса, який успішно застосовують в стратегічних іграх, коли гра ведеться проти розумного супротивника, охочого заподіяти нам найбільший збиток. Проте у ряді випадків доцільно використовувати цей принцип і в статистичних іграх. Мінімаксні принципи, витікаючі з припущення, що природа діє якнайгіршим для статистика чином, є виправданими в стратегічних іграх, але в статистичних іграх вони виражають точку зору дуже обережної людини, що прагне отримати доступне і що не ганяється за нездійсненним, щоб не потерпіти випадково великого збитку. Недоліком мінімаксних принципів слід рахувати також те, що вони не враховують апріорної інформації про стани природи і тим самим обмежують той виграш, який ця інформація може дати. Іншим принципом вибору стратегії, що враховує апріорний розподіл вірогідності, є байесовський принцип. Байесовський принцип, природно, можна застосовувати як до повних, так і до додаткових втрат. Найпростіший випадок вибору рішення в грі з природою — це випадок коли якась із стратегій гравця А перевершує інші («домінує» над ними). Тут виграш домінуючої стратегії при будь-якому стані природи не менше ніж при інших стратегіях, а при деяких — більше; значить потрібний вибирати саме цю стратегію. Якщо навіть в матриці гри з природою немає однієї домінуючої над всіма іншими стратегії, все ж таки корисно подивитися, чи немає в ній дублюючих стратегій і поступливих іншим за всіх умов. Згідно критерію Вальда гра з природою ведеться як гра з розумним, причому агресивним супротивником, що робить все для того, щоб перешкодити нам досягти успіху. Оптимальною вважається стратегія, при якій гарантується виграш у будь-якому випадку не менший, ніж «нижня ціна гри з природою».
Відповідно до критерію Севіджа в умовах невизначеності слід вибирати таку стратегію, яка гарантує мінімальний ризик. Критерій Гурвіца рекомендує при виборі рішення не керуватися ні крайнім песимізмом, ні крайнім, легковажним оптимізмом. В курсовій роботі розглянуто практичне застосування критеріїв Вальда, Севіджа і Гурвіца на прикладі вибору оптимального варіанту будівництва гідроелектростанції і об’єктів інвестування. Відповідно до даних отриманих в розв’язку прикладу 1 можна зробити загальний висновок: використовуючи при розв’язку критерій Вальда і Севіджа була отримана рекомендація про будівництво безшлюзовой гідроелектростанції (А3), використовуючи при розв’язку критерій Гурвіца була отримана рекомендація про будівництво пригребельної гідроелектростанції(![]() ), але якщо ж припустити відомим розподіли вірогідності для різних станів природи, то дана рекомендація про будівництво безшлюзовой гідроелектростанції (А3).
), але якщо ж припустити відомим розподіли вірогідності для різних станів природи, то дана рекомендація про будівництво безшлюзовой гідроелектростанції (А3).
Відповідно до даних отриманих в розв’язку прикладу 2 можна зробити загальний висновок: використовуючи при розв’язку критерій Вальда і Гурвіца була отримана рекомендація про інвестування у підприємство ![]() , використовуючи при розв’язку критерій Севіджа була отримана рекомендація про інвестування у підприємство
, використовуючи при розв’язку критерій Севіджа була отримана рекомендація про інвестування у підприємство ![]() .
.
Список літератури
1. Бутинець Ф.Ф. Економічний аналіз: Навч. посібник для студентів ВНЗ.-Житомир:ПП «Рута», 2003.-680с.
2. Вентцель Е.С. Исследование операций: задачи, принципы, методология.-2-е изд.-М.: Наука. Гл. ред. физ.- мат. литературы, 1988.-208с.
3. Вентцель Е.С. Элементы теории игр. – М.: Физ.-мат. издательство, 1961.- 69с.
4. Гермейер Ю.Б. Игры с непротивоположными интересами.- М.: Главная редакция физ.-мат. литературы из-ва «Наука», 1976.
5. Горелин В.А. Исследование операций: Учебник.- М. «Машиностроение»,1986.-288с.
6. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. -М.: Высшая школа, 1976.
7. Партхасаратхи Т., Рагхаваи Т. Перевод с англ. Доманского П.П. Некоторые вопросы теории игр двух лиц.- М.: «Мир», 1974.-280с.
8. Савицька Г.В. Економічний аналіз діяльності підприємств: Навч. посібник.-2-ге видання, випр. і допов.- К.:Знання, 2005.-662с.
Похожие работы
... методи екологічного виховання необхідно змінювати, чергувати залежно від змісту, мети вивчення теми, рівня підготовки учнів. 2.3 Виховання бережливого ставлення до природи у процесі гри У становленні емоційно-ціннісного, відповідального ставлення молодшого школяра до природи важливу роль відіграє гра. Найважливішим результатом гри є глибока емоційна задоволеність дитини її процесом, що найб ...
... значення має ігра для величезної кількості збиткових, нерозвинених дітей, яких необхідно виховувати сьогодні, оскільки завтра буде пізно. 5. Ігра одночасно - розвиваюча діяльність, принцип, метод і форма життєдіяльності, зона соціалізації, захищеності, самореабілітації, співпраці, співдружності, співтворчості з дорослими, посередник між світом дитини і світом дорослого. 6. Сучасна гуманістична ...
... учнів буде більш раціональною і продуктивною за умови оптимального застосування системи дидактичних ігор. Важливою умовою підвищення ефективності навчального процесу є використання розвивального потенціалу дидактичної гри у початковій школі, яка б допомагала здійснювати оптимальну навчально-пізнавальну діяльність молодших школярів. Проведений аналіз наукової літератури засвідчив, що проблема ...
... , і умова, що дають змогу повніше використовувати можливості учнів. Пізнавальна самостійність формується у різних навчальних ситуаціях: сприйнятті готового матеріалу, спрямованій пізнавальній активності, дослідницькій пізнавальній діяльності. Ігри створюють певний емоційний фон в учнівському колективі, але й потребують певного емоційного настрою. Одним з принципів навчання є позитивне емоційне ...
0 комментариев