Навигация
Метод Монте-Карло в условиях управления рыночными рисками
2. Метод Монте-Карло в условиях управления рыночными рисками.
Метод Монте-Карло, или метод стохастического моделирования (Monte Carlo simulation), основан на моделировании случайных процессов с заданными характеристиками. В отличие от метода исторического моделирования, в методе Монте-Карло изменения цен активов генерируются псевдослучайным образом в соответствии с заданными параметрами распределения, например математическим ожиданием μ и волатильностью σ. Имитируемое распределение может быть, в принципе, любым, а количество сценариев — весьма большим (до нескольких десятков тысяч). Выделяют:
метод Монте-Карло для одного фактора риска;
метод Монте-Карло для портфеля активов.
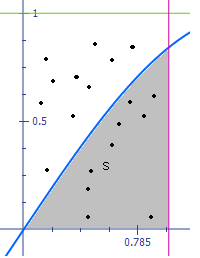
Рассмотрим Метод Монте-Карло для одного фактора риска. Моделирование траектории цен производится по различным моделям. Например, распространенная модель геометрического броуновского движения дает в итоге следующие выражения для моделирования цен S на каждом шаге процесса, состоящего из очень большого количества шагов, охватывающих период Т:
dSt = St (μdt + σdzt), (1)
, где dzt — винеровский случайный процесс.
Воспользовавшись определением винеровского процесса, уравнение (1) можно записать в дискретной форме:
σσ∆St= St-1 (μ∆t + σε√∆t) , (2)
т. е.
St+1 = St + St (μ∆t + σε1√∆t), (3)
St+1 = St+1 + St+1 (μ∆t + σε2√∆t), (4)
ST = St+n.
Если траектория цен состоит из n равных шагов (например, n дней), то один шаг ∆t = 1/n, а случайная величина ε подчиняется стандартному нормальному распределению (μ = 0, σ = 1). Можно использовать и иные модели эволюции цен, например экспоненциальную.
Траектория цен — это последовательность псевдослучайным образом смоделированных цен, начиная от текущей цены и заканчивая ценой на некотором конечном шаге, например на тысячном или десятитысячном. Чем больше число шагов, тем выше точность метода.
Каждая траектория представляет собой сценарий, по которому определяется цена на последнем шаге исходя из текущей цены. Затем производится полная переоценка портфеля по цене последнего шага и расчет изменения его стоимости для каждого сценария. Оценка VaR производится по распределению изменений стоимости портфеля.
Генерация случайных чисел в методе Монте-Карло состоит из двух шагов. Сначала можно воспользоваться генератором случайных чисел, равномерно распределенных на интервале между 0 и 1 (рассмотрено выше). Затем, используя как аргументы полученные случайные числа, вычисляют значения функций моделируемых распределений.
Однако следует помнить, что генераторы случайных чисел работают на детерминированных алгоритмах и воспроизводят так называемые «псевдослучайные числа», поскольку с некоторого момента последовательности этих псевдослучайных чисел начинают повторяться, т. е. они не являются независимыми. В простейших генераторах это происходит уже через несколько тысяч генераций, а в более сложных— через миллиарды генераций. Если массив случайных чисел начинает повторяться слишком быстро, то метод Монте-Карло перестает моделировать случайные, независимые сценарии и оценка VaR начинает отражать ограниченность генератора, а не свойства портфеля. Оптимальное количество шагов в процессе зависит от объема выборки, состава портфеля и сложности составляющих его инструментов и др.
Рассмотрим пример: элементы расчета VaR методом Монте-Карло на современном российском рынке. Для расчета VaR можно использовать различные модификации метода Монте-Карло; в данном случае метод описывается следующим образом:
По ретроспективным данным рассчитываются оценки математического ожидания х и волатильности σ.
С помощью датчика случайных чисел генерируются нормально распределенные случайные числа ε с математическим ожиданием, равным х, и стандартным отклонением σ.
Полученными на предыдущем шаге случайными числами ε заполняется таблица размерностью 500 столбцов на 1000 строк (вообще говоря, размерность таблицы произвольная и зависит, например, от имеющихся вычислительных мощностей, но, чтобы метод обеспечивал приемлемую точность, она должна быть достаточно большой).
Вычисляется траектория моделируемых цен вплоть до S1000 по формуле St= St-1e εt-1, где е — основание натурального логарифма, St— текущая цена (курс) актива.
Производится переоценка стоимости портфеля (состоящего в данном примере из одного актива) по формуле: ∆V= Q (S1000 – S0), где Q — количество единиц актива.
Шаги 4 и 5 выполняются 500 раз для заполнения таблицы 500 х 1000. Полученные 500 значений ∆V сортируются по убыванию (от самого большого прироста до самого большого убытка). Эти ранжированные изменения можно пронумеровать от 1 до 500. В соответствии с желаемым уровнем доверия (1 - α) риск-менеджер может определить VaR как такой максимальный убыток, который не превышается в 500(1 - α) случаях, т. е. VaR равен абсолютной величине изменения с номером, равным 500(1 - α).
Шаги 1-6 повторяются для каждого расчета каждого дневного VaR.
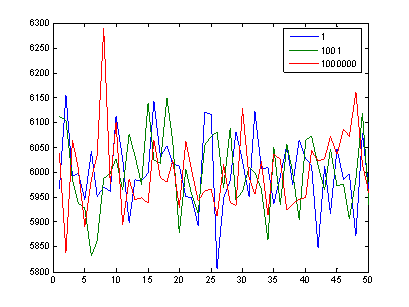
В качестве объекта исследования был выбран индекс РТС. Генерация случайных чисел производилась при помощи встроенного генератора МS Ехсеl.
Метод Монте-Карло является наиболее технически сложным из всех описанных методов расчета VaR. Кроме того, для выполнения расчетов в полном объеме необходимы значительные вычислительные мощности и временные ресурсы. Современные компьютеры пока еще не позволяют обрабатывать информацию в режиме реального времени, как этого требуют трейдеры, если риск-менеджеры хотят устанавливать VaR-лимиты на величину открытых позиций с помощью метода Монте-Карло.
Существует вариант метода Монте-Карло, согласно которому можно не задавать какое-либо конкретное распределение для моделирования цен, а использовать непосредственно исторические данные. Подобно методу исторического моделирования, на основе ретроспективы моделируются гипотетические цены, но их последовательность не является единственной и не ограничена глубиной периода ретроспективы, поскольку выборка производится с возвращением (bootstrap), т. е. возмущение из исторических данных выбирается случайным образом, и каждый раз в выборе участвуют все данные. Такое построение выборки исторических данных позволяет учесть эффект «толстых хвостов» и скачки цен, не строя предположений о виде распределения. Это несомненные достоинства метода, который, в отличие от метода исторического моделирования, позволяет рассмотреть не какую-либо одну траекторию цен (сценарий), а сколь угодно много, что, как правило, повышает точность оценок. Недостатками данной методики являются низкая точность при малых объемах выборки и использование предположения о независимости доходностей во времени.
Теперь рассмотрим метод Монте-Карло для портфеля активов. Чтобы проводить моделирование по Монте-Карло для многофакторного процесса, можно точно так же моделировать каждый из к рассматриваемых факторов исходя из сгенерированных случайных чисел:
dSt,j = μt,j St,j dt + σt,j St,j Sdzt,j, j = 1,2, …, k, (5)
или для дискретного времени:
∆St,j = St-1,j(μj∆t + σjεj√∆t), j = 1,2, …, k. (6)
С целью учета корреляции между факторами необходимо, чтобы случайные величины εi и εj точно так же коррелировали между собой. Для этого используется разложение Холецкого, суть которого состоит в разложении корреляционной матрицы на две (множители Холецкого) и использовании их для вычисления коррелированных случайных чисел.
Корреляционная матрица является симметричной и может быть представлена произведением треугольной матрицы низшего порядка с нулями в верхнем правом углу на такую же транспонированную матрицу. Например, для случая двух факторов имеем:
Отсюда
Коррелированные случайные числа ε1 и ε2 получаются путем перемножения множителя Холецкого и вектора независимых случайных чисел η:
При расчетах необходимо правильно выбрать количество множителей,
чтобы получилась положительно определенная матрица.
Достоинства метода Монте-Карло:
высокая точность расчетов;
высокая точность применительно к инструментам с нелинейными ценовыми характеристиками;
возможность моделирования любых исторических и гипотетических распределений, учет эффекта «толстых хвостов» и скачков цен (вегариска).
Недостатки метода Монте-Карло:
высокая сложность моделей и соответственно высокий риск неадекватности моделей;
высокие требования к вычислительной мощности и значительные затраты времени на проведение расчетов.
Вывод
В данной работе был рассмотрен метод Монте – Карло. Этот метод имитации применим для решения почти всех задач при условии, что альтернативы могут быть выражены количественно. Построение модели начинается с определения функциональных зависимостей в реальной системе, которые в последствии позволяют получить количественное решение, используя теорию вероятности и таблицы случайных чисел.
Модель Монте-Карло не столь формализована и является более гибкой, чем другие имитирующие модели. Причины здесь следующие:
при моделировании по методу Монте-Карло нет необходимости определять, что именно оптимизируется;
нет необходимости упрощать реальность для облегчения решения, поскольку применение ЭВМ позволяет реализовать модели сложных систем;
в программе для ЭВМ можно предусмотреть опережения во времени.
Данный метод является общепризнанным и наилучшим, так как обладает рядом непреодолимых достоинств, в частности использует гипотезу о нормальном распределении доходностей, показывает высокую точность для нелинейных инструментов и устойчив к выбор ретроспективы. К недостаткам можно отнести техническую сложность расчётов и модельный риск.
Список литературы
1. Ильин И. П. «Планирование на предприятии». М: 2002.
2. «Энциклопедия финансового риск-менеджмента» под. ред. Лобанова А. А. М: 2005.
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
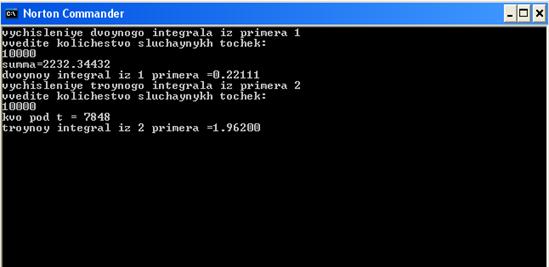
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...

0 комментариев