САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КУРСОВАЯ РАБОТА
ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ МЕТОДОМ МОНТЕ - КАРЛО
Выполнил:
Руководитель:
Саратов, 2009
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. МАТЕМАТИЧЕСКОЕ ОБОСНОВАНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЯ ИНТЕГРАЛА
1.1 Принцип работы метода Монте – Карло
1.2 Применение метода Монте – Карло для вычисления n – мерного интеграла.
1.3 Сплайн – интерполяция 8
1.4 Алгоритм расчета интеграла
2. ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ
2.1 Генератор псевдослучайных чисел применительно к методу Монте – Карло.
2.2 Алгоритм генератора псевдослучайных чисел
2.3 Проверка равномерности распределения генератора псевдослучайных чисел.
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Целью данной работы является создание программного продукта для участия в конкурсе, проводимом группой компаний «Траст» по созданию программных разработок. Для реализации было выбрано следующее технической задание:
Задание 12 Вычисление интегралов методом Монте – Карло.
Цель:
1) Реализация генератора случайных чисел для метода Монте – Карло.
2) Сравнение равномерного распределения и специально разработанного.
3) Вычисление тестового многомерного интеграла в сложной области.
Продукт:
1) Программный код в виде функции на языке С++ или Fortran .
2) Тестовые примеры в виде программы, вызывающие реализованные функции.
3) Обзор использованной литературы.
Для реализации данного технического задания был выбран язык C++. Код реализован в интегрированной среде разработки приложений Borland C++ Builder Enterprises и математически обоснован соответствующий способ вычисления интеграла.
1. МАТЕМАТИЧЕСКОЕ ОБОСНОВАНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЯ ИНТЕГРАЛА 1.1 Принцип работы метода Монте – Карло
Датой рождения метода Монте - Карло признано считать 1949 год, когда американские ученые Н. Метрополис и С. Услам опубликовали статью под названием «Метод Монте - Карло», в которой были изложены принципы этого метода. Название метода происходит от названия города Монте – Карло, славившегося своими игорными заведениями, непременным атрибутом которых являлась рулетка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод.
Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных экономических систем.
Сущность метода состоит в том, что в задачу вводят случайную величину ![]() , изменяющуюся по какому то правилу
, изменяющуюся по какому то правилу ![]() . Случайную величину выбирают таким образом, чтобы искомая в задаче величина
. Случайную величину выбирают таким образом, чтобы искомая в задаче величина ![]() стала математическим ожидание от
стала математическим ожидание от ![]() , то есть
, то есть ![]() .
.
Таким образом, искомая величина ![]() определяется лишь теоретически. Чтобы найти ее численно необходимо воспользоваться статистическими методами. То есть необходимо взять выборку случайных чисел
определяется лишь теоретически. Чтобы найти ее численно необходимо воспользоваться статистическими методами. То есть необходимо взять выборку случайных чисел ![]() объемом
объемом ![]() . Затем необходимо вычислить выборочное среднее
. Затем необходимо вычислить выборочное среднее ![]() варианта случайной величины
варианта случайной величины ![]() по формуле:
по формуле:
 . (1)
. (1)
Вычисленное выборочное среднее принимают за приближенное значение ![]() .
.
Для получения результата приемлемой точности необходимо большое количество статистических испытаний.
Теория метода Монте – Карло изучает способы выбора случайных величин ![]() для решения различных задач, а также способы уменьшения дисперсии случайных величин.
для решения различных задач, а также способы уменьшения дисперсии случайных величин.
Рассмотрим n – мерный интеграл
![]() для
для ![]() . (2)
. (2)
Будем считать, что область интегрирования ![]() , и что
, и что ![]() ограниченное множество в
ограниченное множество в ![]() . Следовательно, каждая точка х множества
. Следовательно, каждая точка х множества ![]() имеет n координат:
имеет n координат: ![]() .
.
Функцию ![]() возьмем такую, что она ограничена сверху и снизу на множестве
возьмем такую, что она ограничена сверху и снизу на множестве ![]() :
: ![]() .
.
Воспользуемся ограниченностью множества ![]() и впишем его в некоторый n – мерный параллелепипед
и впишем его в некоторый n – мерный параллелепипед ![]() , следующим образом:
, следующим образом:
![]() ,
,
где ![]() - минимумы и максимумы, соответственно,
- минимумы и максимумы, соответственно, ![]() - ой координаты всех точек множества
- ой координаты всех точек множества ![]() :
: ![]() .
.
Доопределяем подынтегральную функцию ![]() таким образом, чтобы она обращалась в ноль в точках параллелепипеда
таким образом, чтобы она обращалась в ноль в точках параллелепипеда ![]() , которые не принадлежат
, которые не принадлежат ![]() :
:
![]() (3)
(3)
Таким образом, уравнение (2) можно записать в виде
![]() . (4)
. (4)
Область интегрирования представляет собой n – мерный параллелепипед ![]() со сторонами параллельными осям координат. Данный параллелепипед можно однозначно задать двумя вершинами
со сторонами параллельными осям координат. Данный параллелепипед можно однозначно задать двумя вершинами ![]() , которые имеют самые младшие и самые старшие координаты всех точек параллелепипеда.
, которые имеют самые младшие и самые старшие координаты всех точек параллелепипеда.
Обозначим через ![]() n-мерный вектор, имеющий равномерное распределение в параллелепипеде
n-мерный вектор, имеющий равномерное распределение в параллелепипеде ![]() :
: ![]() , где
, где ![]() .
.
Тогда ее плотность вероятностей ![]() будет определена следующим образом
будет определена следующим образом
 (5)
(5)
Значение подынтегральной функции ![]() от случайного вектора
от случайного вектора ![]() будет случайной величиной
будет случайной величиной ![]() , математическое ожидание
, математическое ожидание ![]() которой является средним значением функции на множестве
которой является средним значением функции на множестве ![]() :
:
![]() . (6)
. (6)
Среднее значение функции на множестве ![]() равняется отношению значения искомого интеграла к объему параллелепипеда
равняется отношению значения искомого интеграла к объему параллелепипеда ![]() :
:
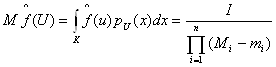 (7)
(7)
Обозначим  объем параллелепипеда
объем параллелепипеда ![]() .
.
Таким образом, значение искомого интеграла можно выразить как произведение математического ожидания функции и объема n- мерного параллелепипеда ![]() :
:
![]() (8)
(8)
Следовательно, необходимо найти значение математического ожидания ![]() . Его приближенное значение можно найти произведя n испытаний, получив, таким образом, выборку
. Его приближенное значение можно найти произведя n испытаний, получив, таким образом, выборку ![]() случайных векторов, имеющих равномерное распределение на
случайных векторов, имеющих равномерное распределение на ![]() . Обозначим
. Обозначим ![]() и
и ![]() . Для оценки математического ожидания воспользуемся результатом
. Для оценки математического ожидания воспользуемся результатом
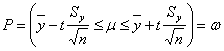 , (9)
, (9)
где ![]() ,
,
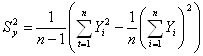 ,
,
![]() - квантиль нормального распределения, соответствующей доверительной вероятности
- квантиль нормального распределения, соответствующей доверительной вероятности ![]() .
.
Умножив двойное неравенство из (9) на ![]() получим интервал для I:
получим интервал для I:
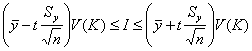 . (10)
. (10)
Обозначим ![]() точечную оценку
точечную оценку ![]() . Получаем оценку (с надежностью
. Получаем оценку (с надежностью ![]() ):
):
![]() . (11)
. (11)
Аналогично можно найти выражение для относительной погрешности ![]() :
:
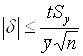 . (12)
. (12)
Если задана целевая абсолютная погрешность ![]() , из (11) можно определить объем выборки, обеспечивающий заданную точность и надежность:
, из (11) можно определить объем выборки, обеспечивающий заданную точность и надежность:
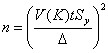 . (13)
. (13)
Если задана целевая относительная погрешность, из (12) получаем аналогичное выражение для объема выборки:
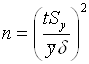 . (14)
. (14)
В данном программном продукте реализована возможность задавать дополнительные ограничения области интегрирования двумя двумерными сплайн – поверхностями (для подынтегральной функции размерности 3). Для задания этих поверхностей используются двумерные сплайны типа гибкой пластинки \4\.
Под сплайном (от англ. spline - планка, рейка) обычно понимают агрегатную функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения. Сплайн – функция имеет следующий вид:
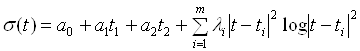 . (15)
. (15)
Исходные данные представляют собой ![]() троек точек
троек точек ![]() .
.
Коэффициенты ![]() и
и ![]() определяются из системы:
определяются из системы:
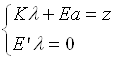 , (16)
, (16)
где ![]() ,
,
![]()
 .
.
Реализованный алгоритм включает следующие шаги:
1) выбирается начальное значение ![]() , разыгрываются случайные векторы из
, разыгрываются случайные векторы из ![]() и определяются
и определяются ![]() и
и ![]() ;
;
2) в зависимости от вида погрешности (абсолютная, относительная) определяется достигнутая погрешность; если она меньше целевой, вычисление прерывается;
3) по формулам (13) или (14) вычисляется новый объем выборки;
4) объем выборки увеличивается на 20%
5) переход к шагу 1;
6) конец.
2. ГЕНЕРАТОР ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ 2.1 Генератор псевдослучайных чисел применительно к методу Монте – Карло.
В любом алгоритме использующем метод Монте – Карло генератор псевдослучайных чисел играет очень важную роль. Степень соответствия псевдослучайных чисел заданному распределению является важным фактором проведения качественных статистических испытаний.
2.2 Алгоритм генератора псевдослучайных чиселВ программе реализован конгруэнтный метод генерации псевдослучайных чисел \3\:
![]() , (17)
, (17)
где ![]() =8192,
=8192,
![]() =67101323.
=67101323.
Авторский код, реализующий защиту от переполнения был, реализован на С++. Перед использование первые три числа последовательности удаляются. Для получении чисел из интервала (0,1) все числа делятся на ![]() .
.
Проверка равномерности распределения псевдослучайных чисел проводилась с помощью стандартного критерия χ2 \2\.
Были использованы 3 последовательности псевдослучайных чисел, определяемых стартовыми значениями 1, 1001, 1000000 длиной 300000.
Интервал (0,1) подразделялся на 50 равных интервалов и программно подсчитывались абсолютные частоты (рис. 1).
Рис. 1
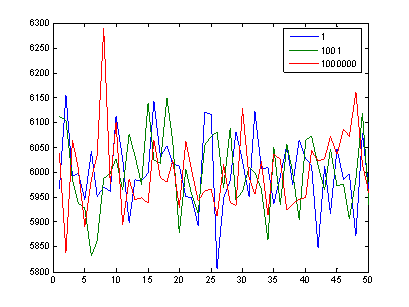
Результаты проверки приведены в Таблице 1.
Таблица 1
| стартовое значение ГСЧ | |||
| 1 | 1001 | 1000000 | |
| хи-квадрат | 44.0533333333333 | 45.007 | 48.618 |
| df | 50 | 50 | 50 |
| p-значение | 0.709735881642893 | 0.673522612551685 | 0.528941919633451 |
Следовательно, равномерность распределения не отвергается на уровне 5%.
ЗАКЛЮЧЕНИЕ
В заключение можно сказать, что поставленная задача была полностью выполнена. То есть на языке С++ были разработаны генератор псевдослучайных чисел, функция рассчитывающая интеграл методом Монте – Карло (Приложение 1); был проведен расчет тестовых многомерных интегралов (Приложение 2); в интегрированной среде разработки приложений Borland C++ Builder Enterprises 7.0 был создан программный продукт «CarloS», реализующий описанные выше алгоритмы (Приложение 3).
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем. – М.: Финансы и статистика, 2001. – 368 с.
2. Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. – М.: Финансы и статистика, 1982. – 278 с.
3. Теннант-Смит Дж. Бейсик для статистиков. – М.: Мир, 1988. – 208 с.
4. Baranger J. Analyse numérique. Hermann, 1991.
5. Маделунг Э. Математический аппарат физики. Справочное руководство. М.: Наука, 1968., с.287.
6. В.Е. Гмурман Теория вероятностей и математическая статистика – М.: Высшая школа, 2003
ПРИЛОЖЕНИЕ 1
ЛИСТИНГИ ОСНОВНЫХ ФУНКЦИЙ
Листинг 1 Функция расчета интеграла
void integral ()
{
// вычисление интеграла методом Монте – Карло
// размерность области интегрирования
unsigned d_int=fun_dim;
//----- 3 d график --------------------------------------------------------
// максимальное число троек
unsigned plot_dim_max=10000;
// матрица троек
pmatd xyz,xyz_tmp;
if (d_int==3) xyz=new matd(plot_dim_max,3);
//-------------------------------------------------------------------------
// индикатор относительной погрешности
mcres.relok=Read1double("error_type.txt");
// целевая погрешность
mcres.dlt_int=Read1double("error_value.txt");
// номер стандартного значения доверительной вероятности (начиная с 0)
int nome_int=Read1double("error_omega.txt");
// ГСЧ
unsigned long b=m_rng*m_rng-d_rng,c,r,i,PSChunk;
// "росток" ГСЧ
mcres.rng_seed=Read1double("rng_seed.txt");
pmatd fun_b, fun_A, con_b, con_A, con_U, con_v, \
a_int, b_int, ba_int, x_int, xyz_top, xyz_bottom;
unsigned j,ii,jj,con_ok;
struct date dat;
struct time tim;
pspl2d sp_top,sp_bottom;
// квантили нормального распределения
double omegas_int[6]={0.9,0.95,0.99,0.999,0.9999,0.99999};
double zs_int[6]={1.64485362695147,1.95996398454005,2.5758293035489, \
3.29052673149191, 3.89059188641317, 4.4171734134667};
mcres.omega_int=omegas_int[nome_int];
mcres.z_int=zs_int[nome_int];
double fun_cd,con_wd,fu_int,con_sum,sum1_int,sum2_int;
// вид интегрируемой функции
// 0 - постоянная
// 1 - линейная
// 2 - квадратичная
mcres.fun_type=Read1double("fun_kind.txt");
// вид системы ограничений
// 0 – отсутствуют (весь параллелепипед)
// 1 - линейные
// 2 - квадратичное
// 3 – сплайн - поверхности
mcres.con_type=Read1double("con_type.txt");
// загрузка параметров интегрируемой функции
switch (mcres.fun_type)
{
case 2: fun_A=new matd("fun_A.txt");
case 1: fun_b=new matd("fun_b.txt");
case 0: fun_cd=Read1double("fun_c.txt");
}
// загрузка параметров ограничений
switch (mcres.con_type)
{
case 3: // сплайн - поверхности
// верхняя
xyz_top=new matd("xyz_top.txt");
// нижняя
xyz_bottom=new matd("xyz_bottom.txt");
// двумерная интерполяция
sp_top=new spl2d(xyz_top);
sp_bottom=new spl2d(xyz_bottom);
break;
case 2: // квадратичная функция ограничений
con_U=new matd("con_U.txt");
con_v=new matd("con_v.txt");
con_wd=Read1double("con_w.txt");
break;
case 1: // линейные ограничения
con_b=new matd("con_b.txt"); con_A=new matd("con_A.txt");
}
// объемлющий параллелепипед
a_int=new matd("con_xmin.txt");
b_int=new matd("con_xmax.txt");
// разность границ параллелепипеда
ba_int=new matd;
ba_int=&(*b_int - (*a_int));
// аргумент интегрируемой функции
x_int=new matd(d_int,1);
//объем объемлющего параллелепипеда
mcres.V0_int=1;
for (j=1; j <= d_int; j++)
{
if (_p(ba_int,j,1) <= 0)
{
DbBox("Нижняя граница объемлющего параллелепипеда выше верхней для \
координаты ",j);
goto clean_exit;
}
mcres.V0_int=mcres.V0_int*_p(ba_int,j,1);
}
// начальный объем выборки
mcres.n1_int=10000;
// основной цикл для достижения заданной точности
// число итераций, потребовавшихся для достижения заданной точности
mcres.n_ite=0;
getdate(&dat); gettime(&tim); mcres.t_start=dostounix(&dat,&tim);
WaitForm->Show();
while (1)
{
mcres.n_ite++;
WaitForm->Edit1->Text=mcres.n_ite;
WaitForm->Edit2->Text=mcres.n1_int;
WaitForm->ProgressBar1->Position=0;
WaitForm->Refresh();
// генерация случайных точек и накопление суммы
sum1_int=0; sum2_int=0;
mcres.in_G_int=0;
PSChunk=long(mcres.n1_int/50.0);
// запуск ГСЧ
r=mcres.rng_seed;
for (i=1; i < 3; i++)
{
c=int(r/m_rng);
r=b*c+m_rng*(r-m_rng*c);
if (r > d_rng) r=r-d_rng;
}
for (i=1; i <= mcres.n1_int; i++)
{
// случайный вектор
for (j=1; j <= d_int; j++)
{
// случайное число
c=int(r/m_rng);
r=b*c+m_rng*(r-m_rng*c);
if (r > d_rng) r=r-d_rng;
_p(x_int,j,1)=_p(a_int,j,1)+_p(ba_int,j,1)*double(r)/d_rng;
}
// прогресс
if (!(i % PSChunk))
{
WaitForm->ProgressBar1->Position=100.0*(i-1)/(mcres.n1_int-1);
WaitForm->Refresh();
}
// проверка ограничения
con_ok=1;
switch (mcres.con_type)
{
case 3: // сплайн – поверхности
if ((_p(x_int,3,1) < sp_bottom->f(_p(x_int,1,1), \
_p(x_int,2,1)))||(_p(x_int,3,1) > sp_top->f(_p(x_int,1,1),_p(x_int,2,1)))) con_ok=0;
break;
case 2: // квадратичная функция ограничений
con_sum=0;
for (ii=1; ii <= d_int; ii++)
for (jj=1; jj <= d_int; jj++)
if (_p(con_U,ii,jj) != 0)
con_sum += _p(x_int,ii,1)*_p(con_U,ii,jj)*_p(x_int,jj,1);
for (ii=1; ii <= d_int; ii++)
if (_p(con_v,ii,1) != 0)
con_sum += _p(con_v,ii,1)*_p(x_int,ii,1);
if (con_sum > con_wd) con_ok=0;
break;
case 1: // линейная функция ограничений
for (ii=1; ii <= con_A->nl; ii++)
{
con_sum=0;
for (jj=1; jj <= d_int; jj++)
con_sum += _p(con_A,ii,jj)*_p(x_int,jj,1);
if (con_sum > _p(con_b,ii,1)) { con_ok=0; break; }
}
}
fu_int=0;
if (con_ok != 0)
{
mcres.in_G_int++;
// точки 3d графика
if (d_int==3)
if (mcres.in_G_int <= plot_dim_max)
{
_p(xyz,mcres.in_G_int,1)=_p(x_int,1,1);
_p(xyz,mcres.in_G_int,2)=_p(x_int,2,1);
_p(xyz,mcres.in_G_int,3)=_p(x_int,3,1);
}
// значение интегрируемой функции
switch (mcres.fun_type)
{
case 2: // квадратичный член
for (ii=1; ii <= d_int; ii++)
for (jj=1; jj <= d_int; jj++)
if (_p(fun_A,ii,jj) != 0)
fu_int += _p(x_int,ii,1)*_p(fun_A,ii,jj)*_p(x_int,jj,1);
case 1: // линейный член
for (ii=1; ii <= d_int; ii++)
if (_p(fun_b,ii,1) != 0)
fu_int += _p(fun_b,ii,1)*_p(x_int,ii,1);
case 0: // постоянная
fu_int += fun_cd;
}
}
sum1_int+=fu_int; sum2_int+=fu_int*fu_int;
}
// оценка мат. ожидания и дисперсии
mcres.f1_int=sum1_int/mcres.n1_int;
mcres.vari_int=(sum2_int-sum1_int*sum1_int/mcres.n1_int)/(mcres.n1_int-1);
// расчет погрешности
if (mcres.relok==0)
{
// абсолютная погрешность
mcres.deltar=mcres.V0_int*mcres.z_int*sqrt(mcres.vari_int/mcres.n1_int);
}
else
{
// относительная погрешность
if (mcres.f1_int!=0)
{
mcres.deltar=mcres.z_int/fabs(mcres.f1_int)*sqrt(mcres.vari_int/mcres.n1_int);
}
else
{
// форма результатов
mcres.inte_int=0;
mcres.deltar=0;
getdate(&dat); gettime(&tim); mcres.t_end=dostounix(&dat,&tim);
mcres.t_calc=mcres.t_end-mcres.t_start;
InfoBox("Оценка интеграла = 0 (выбрана относ. погрешность), вычисление \
прервано.");
ResultForm->Show();
WaitForm->Close();
goto clean_exit;
}
}
WaitForm->Edit3->Text=mcres.deltar;
WaitForm->Refresh();
if (mcres.deltar < mcres.dlt_int)
{
// точность достаточна
mcres.inte_int=mcres.V0_int*mcres.f1_int;
getdate(&dat); gettime(&tim); mcres.t_end=dostounix(&dat,&tim);
mcres.t_calc=mcres.t_end-mcres.t_start;
ResultForm->Show();
break;
}
// вычисление нового объема выборки
if (mcres.relok==0)
{
// абс. погрешность
mcres.n1_int=ceil(mcres.vari_int*pow(mcres.V0_int*mcres.z_int/mcres.dlt_int,2));
}
else
{
// отн.погрешность
mcres.n1_int=ceil(mcres.vari_int*pow(mcres.z_int/mcres.dlt_int/mcres.f1_int,2));
}
// корректировка объема выборки в большую сторону
//для сокращения числа итераций
mcres.n1_int=1.2*mcres.n1_int;
// минимальный объем выборки
if (mcres.n1_int < 1000) mcres.n1_int=1000;
} // конец основного цикла
WaitForm->Close();
// 3d график
if (d_int==3)
{
if (mcres.in_G_int==0)
{
// множество точек пусто
Zero_File("xyz.txt");
}
else
if (mcres.in_G_int < xyz->nl)
{
// точек не набралось, чтобы заполнить матрицу
xyz_tmp=new matd(mcres.in_G_int,3);
for (i=1; i <= mcres.in_G_int; i++)
{
_p(xyz_tmp,i,1)=_p(xyz,i,1);
_p(xyz_tmp,i,2)=_p(xyz,i,2);
_p(xyz_tmp,i,3)=_p(xyz,i,3);
}
xyz_tmp->txprint("xyz.txt");
delete xyz_tmp;
}
else
{
// вся матрица заполнена
xyz->txprint("xyz.txt");
}
} // конец d_int==3
clean_exit:
// очистка памяти
if (d_int==3) delete xyz;
switch (mcres.fun_type)
{
case 2: delete fun_A;
case 1: delete fun_b;
}
switch (mcres.con_type)
{
case 3: delete xyz_top,xyz_bottom,sp_top,sp_bottom; break;
case 2: delete con_U,con_v; break;
case 1: delete con_b,con_A;
}
delete a_int,b_int,ba_int,x_int;
} //integral
Листинг 2 структура для хранения результатов расчета интеграла
struct mcres_struct
{
// индикатор относительной погрешности
int relok;
// целевая погрешность
double dlt_int;
// достигнутая погрешность
double deltar;
// доверительная вероятность
double omega_int;
// квантиль норм. распределения
double z_int;
// "росток" ГСЧ
unsigned long rng_seed;
// ÷число итераций, потребовавшихся для достижения заданной точности
unsigned n_ite;
// объем выборки на последней итерации
unsigned long n1_int;
// число точек попавших в область интегрирования
unsigned in_G_int;
// интеграл
double inte_int;
// объем объемлющего параллелепипеда
double V0_int;
// выборочное среднее
double f1_int;
// выборочная дисперсия
double vari_int;
// время начала счета
time_t t_start;
// время окончания счета
time_t t_end;
// продолжительность вычисления интеграла
time_t t_calc;
// вид интегрируемой функции
int fun_type;
// вид системы огрничений
int con_type;
}; // mcres_struct
ПРИЛОЖЕНИЕ 2
ТЕСТОВЫЕ ПРИМЕРЫ
Пример 1 Интеграл от квадратичной функции по 3-мерному симплексу.
Точное значение интеграла:
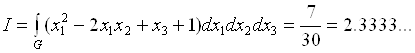
![]()
Приближенное значение ![]() найдено для целевой абсолютной погрешности 0.00001.
найдено для целевой абсолютной погрешности 0.00001.
Погрешность: 0.000034416630896 или 0.014749984670 %.
Примеры 2-10 Объемы многомерных шаров
Точные и приближенные объемы многомерных шаров ![]() приведены в следующей таблице.
приведены в следующей таблице.
|
| Объем точный[1] | Объем | Оценка CarloS[3] | Относительная погрешность, % |
| 2 |
| 3.1415926535897932385 | 3.1504 | 0.280346543342 |
| 3 |
| 4.1887902047863909846 | 4.2032 | 0.344008520578 |
| 4 |
| 4.9348022005446793096 | 4.98099547511312 | .936071451118 |
| 5 |
| 5.2637890139143245968 | 5.18913116403891 | -1.4183290720439 |
| 6 |
| 5.1677127800499700296 | 5.16153372226575 | -.1195704569352 |
| 7 |
| 4.7247659703314011698 | 4.70163814726423 | -.4895019819476 |
| 8 |
| 4.0587121264167682184 | 3.98117943332154 | -1.9102782035357 |
| 9 |
| 3.2985089027387068695 | 3.30542485033746 | .209668908064 |
| 10 |
| 2.5501640398773454440 | 2.55096385956571 | .31363460384e-1 |
[1] Источник [5], с. 287.
[2] Вычислено в Maple (20 значащих цифр).
[3] Расчет с целевой относительной погрешностью 2%
Похожие работы
... , разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) и по ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
... значения интеграла, основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями и , т.е. , (34) Тогда (35) 5. Вычисление интегралов методом Монте-Карло Пусть нам нужно вычислить интеграл: (36) В случае, когда методы Ньютона-Котеса и Гаусса работают плохо, приходится обращаться к вероятностным ...
... в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.). Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой а: (1) ...


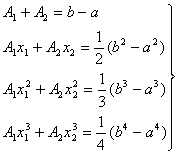




0 комментариев