Навигация
Сущность метода Монте-Карло и моделирование случайных величин
Введение
Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин.
Датой рождение метода Монте-Карло принято считать 1949 г., когда появилась статья под названием «Метод Монте-Карло» (Н. Метрополис, С. Улам). Создателями этого метода считают американских математиков Дж. Неймана и С. Улама. В нашей стране первые статьи были опубликованы в 1955–56 гг. (В.В. Чавчанидзе, Ю.А. Шрейдер, В.С. Владимиров)
Однако теоретическая основа метода была известна давно. Кроме того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т.е. фактически методом Монте-Карло. Однако до появления ЭВМ этот метод не мог найти сколько-нибудь широкого применения, так как моделировать случайные величины вручную – очень трудоёмкая работа. Таким образом, возникновение метода Монте-Карло как весьма универсального численного метода стало возможным только благодаря появлению ЭВМ.
Само название «Монте-Карло» происходит от города Монте-Карло в княжестве Монако, знаменитого своим игорным домом, а одним из простейших механических приборов для получения случайных величин является рулетка.
Первоначально метод Монте-Карло использовался главным образом для решения задач нейтронной физики, где традиционные численные методы оказались малопригодными. Далее его влияние распространилось на широкий круг задач статистической физики, очень разных по своему содержанию. К разделам науки, где всё в большей мере используется метод Монте-Карло, следует отнести задачи теории массового обслуживания, задачи теории игр и математической экономики, задачи теории передачи сообщений при наличии помех и ряд других.
Метод Монте-Карло оказал и продолжает оказывать существенное влияние на развитие методов вычислительной математики и при решении многих задач успешно сочетается с другими вычислительными методами и дополняет их. Его применение оправдано в первую очередь в тех задачах, которые допускают теоретико-вероятностное описание. Это объясняется как естественность получения ответа с некоторой заданной вероятностью в задачах с вероятностным содержанием, так и существенным упрощением процедуры решения.
В подавляющем большинстве задач, решаемых методами Монте-Карло, вычисляют математические ожидания некоторых случайных величин. Так как чаще всего математические ожидания представляют собой обычные интегралы, в том числе и кратные, то центральное положение в теории методов Монте-Карло занимают методы вычисления интегралов.
1. Теоретическая часть
1.1 Сущность метода Монте-Карло и моделирование случайных величин
Предположим, что нам необходимо вычислить площадь плоской фигуры ![]() . Это может быть произвольная фигура, заданная графически или аналитически (связная или состоящая из нескольких частей). Пусть это будет фигура, заданная на рис. 1.1.
. Это может быть произвольная фигура, заданная графически или аналитически (связная или состоящая из нескольких частей). Пусть это будет фигура, заданная на рис. 1.1.
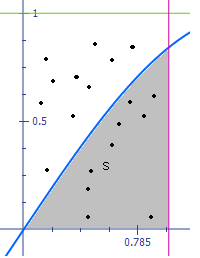
Рис. 1.1
Предположим, что эта фигура расположена внутри единичного квадрата.
Выберем внутри квадрата ![]() случайных точек. Обозначим через
случайных точек. Обозначим через ![]() число точек, попавших внутрь фигуры
число точек, попавших внутрь фигуры ![]() . Геометрически видно, что площадь фигуры
. Геометрически видно, что площадь фигуры ![]() приближенно равна отношению
приближенно равна отношению ![]() . Причем, чем больше число
. Причем, чем больше число ![]() , тем больше точность этой оценки.
, тем больше точность этой оценки.
Для того чтобы выбирать точки случайно, необходимо перейти к понятию случайная величина. Случайная величина ![]() непрерывная, если она может принимать любое значение из некоторого интервала
непрерывная, если она может принимать любое значение из некоторого интервала ![]() .
.
Непрерывная случайная величина ![]() определяется заданием интервала
определяется заданием интервала ![]() , содержащего возможные значения этой величины, и функции
, содержащего возможные значения этой величины, и функции ![]() , которая называется плотностью вероятностей случайной величины
, которая называется плотностью вероятностей случайной величины ![]() (плотностью распределения
(плотностью распределения ![]() ). Физический смысл
). Физический смысл ![]() следующий: пусть
следующий: пусть ![]() - произвольный интервал, такой что
- произвольный интервал, такой что ![]() , тогда вероятность того, что
, тогда вероятность того, что ![]() окажется в интервале
окажется в интервале ![]() , равна интегралу
, равна интегралу
![]() (1.1)
(1.1)
Множество значений ![]() может быть любым интервалом (возможен случай
может быть любым интервалом (возможен случай ![]() ). Однако плотность
). Однако плотность ![]() должна удовлетворять двум условиям:
должна удовлетворять двум условиям:
1) плотность ![]() положительна:
положительна:
![]() ; (1.2)
; (1.2)
2) интеграл от плотности ![]() по всему интервалу
по всему интервалу ![]() равен 1:
равен 1:
![]() (1.3)
(1.3)
Математическим ожиданием непрерывной случайной величины называется число
![]() (1.4)
(1.4)
Дисперсией непрерывной случайной величины называется число:
![]()
Нормальной случайной величиной называется случайная величина ![]() , определённая на всей оси
, определённая на всей оси ![]() и имеющая плотность
и имеющая плотность
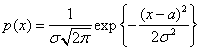 (1.5)
(1.5)
где ![]() - числовые параметры
- числовые параметры
Любые вероятности вида ![]() легко вычисляются с помощью таблицы, в которой приведены значения функции
легко вычисляются с помощью таблицы, в которой приведены значения функции
![]() , называемой обычно интегралом вероятностей.
, называемой обычно интегралом вероятностей.
Согласно (1.1)
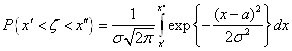
В интеграле сделаем замену переменной ![]() , тогда получим
, тогда получим
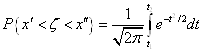 ,
,
где ![]() Отсюда следует, что
Отсюда следует, что ![]() Также
Также ![]()
Нормальные случайные величины очень часто встречаются при исследовании самых различных по своей природе вопросов.
Выбрав ![]() ,
, ![]() , найдём
, найдём ![]() . Следовательно,
. Следовательно,
![]() (1.6)
(1.6)
Вероятность ![]() настолько близка к 1, что иногда последнюю формулу интерпретируют так: при одном испытании практически невозможно получить значение
настолько близка к 1, что иногда последнюю формулу интерпретируют так: при одном испытании практически невозможно получить значение ![]() , отличающееся от
, отличающееся от ![]() больше чем на
больше чем на ![]() .
.
Проводя большое количество опытов, и получая большое количество случайных величин можно воспользоваться центральной предельной теоремой теории вероятностей. Эта теорема впервые была сформулирована П. Лапласом. Обобщением этой теоремы занимались многие выдающиеся математики, в том числе П.Л. Чебышёв, А.А. Марков, А.М. Ляпунов. Её доказательство достаточно сложно.
Рассмотрим ![]() одинаковых независимых случайных величин
одинаковых независимых случайных величин ![]() , так что распределения вероятностей этих величин совпадают. Следовательно, их математические ожидания и дисперсии также совпадают. Величины эти могут быть как непрерывными, так и дискретными.
, так что распределения вероятностей этих величин совпадают. Следовательно, их математические ожидания и дисперсии также совпадают. Величины эти могут быть как непрерывными, так и дискретными.
Обозначим
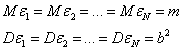
Сумму всех этих величин обозначим через ![]()
Используя соотношения
![]()
получаем
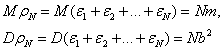
Рассмотрим теперь нормальную случайную величину ![]() с такими же параметрами:
с такими же параметрами: ![]() .
.
В центральной предельной теореме утверждается, что для любого интервала ![]() при больших
при больших ![]()
![]()
Смысл этой теоремы в том, что сумма ![]() большого числа одинаковых случайных величин приближенно нормальна. На самом деле эта теорема справедлива при гораздо более широких условиях: все слагаемые не обязаны быть одинаковыми и независимыми; существенно только, чтобы отдельные слагаемые не играли большой роли в сумме. Эта теорема оправдывает часто встречающиеся нормальные случайные величины. В самом деле, когда встречается суммарное воздействие большого числа незначительных случайных факторов, результирующая случайная величина оказывается нормальной.
большого числа одинаковых случайных величин приближенно нормальна. На самом деле эта теорема справедлива при гораздо более широких условиях: все слагаемые не обязаны быть одинаковыми и независимыми; существенно только, чтобы отдельные слагаемые не играли большой роли в сумме. Эта теорема оправдывает часто встречающиеся нормальные случайные величины. В самом деле, когда встречается суммарное воздействие большого числа незначительных случайных факторов, результирующая случайная величина оказывается нормальной.
Используя эти данные из теории вероятностей можно перейти к описанию общей схемы метода Монте-Карло. Допустим, что требуется вычислить какую-то неизвестную величину ![]() . Попытаемся придумать такую случайную величину
. Попытаемся придумать такую случайную величину ![]() , чтобы
, чтобы ![]() . Пусть при этом
. Пусть при этом ![]() .
.
Рассмотрим ![]() независимых случайных величин
независимых случайных величин ![]() распределения которых совпадают с распределением
распределения которых совпадают с распределением ![]() . Если
. Если ![]() достаточно велико, то, согласно центральной предельной теореме, распределение суммы
достаточно велико, то, согласно центральной предельной теореме, распределение суммы ![]() будет приблизительно нормальным с параметрами
будет приблизительно нормальным с параметрами ![]() . Из (1.6) следует, что
. Из (1.6) следует, что ![]() .
.
Последнее соотношение перепишем в виде:
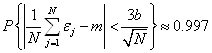 (1.7)
(1.7)
Это соотношение даёт и метод расчёта ![]() , и оценку погрешности.
, и оценку погрешности.
В самом деле, найдём ![]() значений случайной величины
значений случайной величины ![]() . Из (1.7) видно, что среднеарифметическое этих значений будет приближенно равно
. Из (1.7) видно, что среднеарифметическое этих значений будет приближенно равно ![]() . С большой вероятностью погрешность приближения не превосходит величины
. С большой вероятностью погрешность приближения не превосходит величины ![]() . Эта погрешность стремится к нулю с ростом
. Эта погрешность стремится к нулю с ростом ![]() . На практике часто используют не оценку сверху
. На практике часто используют не оценку сверху ![]() , а на вероятную ошибку, которая приближенно равна
, а на вероятную ошибку, которая приближенно равна ![]() Именно такой обычно порядок фактической погрешности расчёта, которая равна
Именно такой обычно порядок фактической погрешности расчёта, которая равна
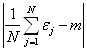 .
.
Для получения случайных чисел используют обычно три способа: таблицы случайных величин, генераторы случайных чисел и метод псевдослучайных чисел.
Таблицы случайных чисел используют предпочтительно при расчётах вручную. Определяющую роль в этом играют два факта: 1) при использовании ЭВМ легче и удобней воспользоваться генератором случайных чисел, получаемых тут же, чем загружать из памяти значения таблицы, которая к тому же, будет занимать там место. 2) При подсчёте вручную нет необходимости использовать ЭВМ, так как часто необходимо выяснить лишь порядок искомой величины.
Генераторы случайных чисел анализируют какой-либо процесс, доступный для них (шумы в электронных лампах, скачки напряжения) и составляют последовательность из 0 и 1, из которых составляются числа с определёнными разрядами, однако такой метод получения случайных величин имеет свои недостатки. Во-первых, трудно проверить вырабатываемые числа. Проверки приходится делать периодически, так как из-за каких-либо неисправностей может возникнуть так называемый дрейф распределения (нули и единицы в каком-либо из разрядов станут появляться не одинаково часто). Во-вторых, обычно все расчёты на ЭВМ проводятся несколько раз, чтобы исключить возможность сбоя. Но воспроизвести те же самые случайные числа невозможно, если их только не запоминать по ходу счёта. А если запоминать, то снова появляется случай таблиц.
Таким образом, самым эффективным способом получения случайных чисел – это использование псевдослучайных чисел.
Числа, получаемые по какой-либо формуле и имитирующие значения случайной величины ![]() , называются псевдослучайными числами.
, называются псевдослучайными числами.
Первый алгоритм для получения псевдослучайных чисел был предложен Дж. Нейманом. Он называется методом середины квадратов.
Пусть задано 4-значное число ![]() . Возведём его квадрат. Получим 8-значное число
. Возведём его квадрат. Получим 8-значное число ![]() . Выберем 4 средние цифры этого числа и положим
. Выберем 4 средние цифры этого числа и положим ![]() .Далее
.Далее ![]() и т.д.
и т.д.
Но этот алгоритм не оправдал себя, так как получается слишком много малых значений. Поэтому были разработаны другие алгоритмы. Наибольшее распространение получил алгоритм, называемый методом сравнений (Д. Лемер): определяется последовательность целых чисел ![]() , в которой начальное число
, в которой начальное число ![]() задано, а все последующие числа
задано, а все последующие числа ![]() вычисляются по одной и той же формуле
вычисляются по одной и той же формуле
![]() при
при ![]() (1.8)
(1.8)
По числам ![]() вычисляются псевдослучайные числа
вычисляются псевдослучайные числа
![]() (1.9)
(1.9)
Формула (1.8) означает, что число ![]() равно остатку, полученному при делении
равно остатку, полученному при делении ![]() на
на ![]() , такой остаток называют наименьшим положительным вычетом по модулю
, такой остаток называют наименьшим положительным вычетом по модулю ![]() Формулы (1.8), (1.9) легко реализовать на ЭВМ.
Формулы (1.8), (1.9) легко реализовать на ЭВМ.
Достоинства метода псевдослучайных чисел довольно очевидны. Во-первых, на получение каждого числа затрачивается всего несколько простых операций, так что скорость генерирования случайных чисел имеет тот же порядок, что и скорость работы ЭВМ. Во-вторых, программа занимает не так много места в памяти. В-третьих, любое из чисел ![]() может быть легко воспроизведено. В-четвёртых, необходимо лишь один раз проверить «качество» такой последовательности, затем её можно много раз безбоязненно использовать при расчёте однотипных задач.
может быть легко воспроизведено. В-четвёртых, необходимо лишь один раз проверить «качество» такой последовательности, затем её можно много раз безбоязненно использовать при расчёте однотипных задач.
Единственный недостаток метода – ограниченность количества псевдослучайных чисел, так как если последовательность чисел ![]() вычисляется на ЭВМ по формуле вида
вычисляется на ЭВМ по формуле вида
![]()
то эта последовательность обязательно периодическая. Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел.
Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет случайная величина ![]() , равномерно распределённая в
, равномерно распределённая в ![]() . Процесс нахождения значения какой-либо случайной величины
. Процесс нахождения значения какой-либо случайной величины ![]() путём преобразования одного или нескольких значений
путём преобразования одного или нескольких значений ![]() называется разыгрыванием случайной величины
называется разыгрыванием случайной величины ![]() .
.
Допустим, что необходимо получать значения случайной величины ![]() , распределённой в интервале
, распределённой в интервале ![]() , с плотностью
, с плотностью ![]() . Докажем, что значения
. Докажем, что значения ![]() можно находить из уравнения
можно находить из уравнения
![]() (1.10)
(1.10)
т.е. выбрав очередное значение ![]() , надо решить уравнение (1.10) и найти очередное значение
, надо решить уравнение (1.10) и найти очередное значение ![]() .
.
Для доказательства рассмотрим функцию
![]() .
.
Из общих свойств плотности (1.2), (1.3) следует, что
![]()
Значит, функция ![]() монотонно возрастает от 0 до 1, и любая прямая
монотонно возрастает от 0 до 1, и любая прямая ![]() , где
, где ![]() , пересекает график
, пересекает график ![]() в одной единственной точке, абсциссу которой мы и принимаем за
в одной единственной точке, абсциссу которой мы и принимаем за ![]() . Таким образом, уравнение (1.10) всегда имеет одно и только одно решение.
. Таким образом, уравнение (1.10) всегда имеет одно и только одно решение.
Выберем теперь произвольный интервал ![]() , содержащийся внутри
, содержащийся внутри ![]() . Точкам этого интервала
. Точкам этого интервала ![]() отвечают ординаты кривой
отвечают ординаты кривой ![]() , удовлетворяющие неравенству
, удовлетворяющие неравенству ![]() .
.
Поэтому, если ![]() принадлежит интервалу
принадлежит интервалу ![]() , то
, то ![]() принадлежит интервалу
принадлежит интервалу ![]() , и наоборот. Значит
, и наоборот. Значит ![]()
Так как ![]() равномерно распределена в
равномерно распределена в ![]() , то
, то
![]() ,
,
итак
![]() ,
,
а это и означает, что случайная величина ![]() , являющаяся корнем уравнения (1.10), имеет плотность вероятностей
, являющаяся корнем уравнения (1.10), имеет плотность вероятностей ![]() .
.
Может оказаться, что разрешить уравнение (1.10) относительно ![]() трудно, например, в случаях, когда интеграл от
трудно, например, в случаях, когда интеграл от ![]() не выражается через элементарные функции или когда плотность
не выражается через элементарные функции или когда плотность ![]() задана графически. Предположим, что случайная величина
задана графически. Предположим, что случайная величина ![]() определена на конечном интервале
определена на конечном интервале ![]() и плотность её ограничена
и плотность её ограничена ![]() .
.
Разыгрывать значение ![]() можно следующим образом:
можно следующим образом:
1) выбираются два значения ![]() и
и ![]() случайной величины
случайной величины ![]() и строится случайная точка
и строится случайная точка ![]() с координатами
с координатами
![]()
2) если точка ![]() лежит под кривой
лежит под кривой ![]() , то полагаем
, то полагаем ![]() , если же точка
, если же точка ![]() лежит над кривой
лежит над кривой ![]() , то пара
, то пара ![]() отбрасывается и выбирается новое значение.
отбрасывается и выбирается новое значение.
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
... в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.). Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой а: (1) ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...
... опыт», учится на своих и чужих ошибках и постепенно выучиваться принимать правильные решения – если не оптимальные, то почти оптимальные. Попробуем проиллюстрировать процесс имитационного моделирования через сравнение с классической математической моделью. Этапы процесса построения математической модели сложной системы: 1. Формулируются основные вопросы о поведении ...





0 комментариев