Навигация
Методика введения показательной функции
2.2 Методика введения показательной функции
Изучение темы «Показательная функция» в курсе алгебры и начала анализа предусматривает знакомство учащихся с вопросами:
Обобщение понятия о степени; понятие о степени с иррациональным показателем; решение иррациональных уравнений и их систем; показательная функция, ее свойства и график; основные показательные тождества:
![]() ;
; ![]() ;
;
тождественные преобразования показательных выражений; решение показательных уравнений, неравенств и систем; понятие об обратной функции; функция, ее свойства и график;
Основная цель – привести в систему и обобщить имеющиеся у учащихся сведения о степени, ознакомить их с показательной функцией и ее свойствами, научить решать несложные показательные уравнения, их системы (содержащие также и иррациональные уравнения).
Рассматриваются свойства и график показательной функции. Систематизация свойств указанной функции осуществляется в соответствии с принятой схемой исследования функций. Приведен краткий обзор свойств степенной функции ![]() в зависимости от различных значений показателя р.
в зависимости от различных значений показателя р.
Особое внимание уделяется показательной функции как той математической модели, которая находит наиболее широкое применение при изучении процессов и явлений окружающей действительности. Рассматриваются примеры различных процессов (например, радиоактивный распад, изменение температуры тела); показывается, что решение дифференциальных уравнений, описывающих эти процессы, является показательная функция. В связи с этим для показательной функции дается формула производной, вывод которой проводится с привлечением интуитивных представлений учащихся.
В ходе изучения свойств показательной функцией учащиеся систематически решают простейшие показательные уравнения и неравенства, а также иррациональные уравнения. По мере закрепления соответствующих умений целесообразно также предлагать им уравнения и неравенства, сводящиеся к простейшим в результате несложных тождественных преобразований.
Появление вычислительной техники в школе открыло возможности, которые связаны с интеграцией новых информационных технологий в учебный процесс по различным школьным предметам. В настоящее время применение различных видов прикладного программного обеспечения носит преимущественно эпизодический характер.
На изучение темы отводится 6 часов. Поурочное планирование следующее:
1 урок – лекция;
2 урок – практикум по решению задач.
Решение показательных уравнений и неравенств:
1 урок – решение типовых задач;
2 урок – практикум по решению задач;
3 урок – практикум по решению задач.
4 урок – закрепление изученного материала по теме «Показательная функция».
Ознакомление учащихся с показательной функцией начиная с изучения свойств степеней.
Курс алгебры знакомит учащихся с понятием степени с рациональным показателем. Таким образом для любого основания степени ![]() (где
(где ![]() ,
, ![]() ). Можно построить функцию:
). Можно построить функцию: ![]() ,
, ![]() , область определения которой – множество действительных чисел, необходимо ввести определение, степени с иррациональным показателем. Используемое свойство степени с основным, например, большим единицы (возрастании), рациональное приближение иррационального числа α: r1< α< r2. Исходя из графического изображения зависимости показателя степени и значения степени, показывается, что найдется такое значение y, которое будет наибольшим среди всех ar1 и наименьшим среди всех ar2, которое можно считать значением aα.
, область определения которой – множество действительных чисел, необходимо ввести определение, степени с иррациональным показателем. Используемое свойство степени с основным, например, большим единицы (возрастании), рациональное приближение иррационального числа α: r1< α< r2. Исходя из графического изображения зависимости показателя степени и значения степени, показывается, что найдется такое значение y, которое будет наибольшим среди всех ar1 и наименьшим среди всех ar2, которое можно считать значением aα.
Затем формируется определение показательной функции: функция, заданная формулой y=ax(![]() ,
, ![]() ), называется показательной функцией с основанием a, и формулируемые основные свойства: D(ax)=R; E(ax)=RТ; ax возрастает при a>1 и ax убывает при 0<a<1; напоминаются основные свойства степеней. Т.о. показательная функция есть систематизация, обобщение и расширение знаний учащихся о свойствах степени.
), называется показательной функцией с основанием a, и формулируемые основные свойства: D(ax)=R; E(ax)=RТ; ax возрастает при a>1 и ax убывает при 0<a<1; напоминаются основные свойства степеней. Т.о. показательная функция есть систематизация, обобщение и расширение знаний учащихся о свойствах степени.
В качестве приложения свойств показательной функции рассматриваются решения простейших показательных уравнений и неравенств.
Функция – новый математический объект для учащихся.
1. Область определения показательной функции множество действительных чисел.
2. Область значений показательной функции множество действительных чисел.
3. При а>1 функция возрастает на всей числовой прямой.
4. При 0<а<1 функция убывает на всей числовой прямой.
5. При любых действительных х и у справедливо равенство а х *ау=аху.
6. Область значения функции у=3х+1 числовой промежуток (-4; 4).
7. Область определения показательной функции у=а х промежуток (-4; 4).
8. Функция у=0,2 х убывает на R.
9. Функция у=0,7х возрастает на R.
10. График функции у=2 х проходит через точку (0; 1).
2.3 Методические особенности изучения степенной функции
Степень с рациональным показателем является наиболее важным этапом изучения степенной функции ![]() , где x>0, α
, где x>0, α![]() , и наиболее трудным для восприятия материалом в школьном курсе алгебры.
, и наиболее трудным для восприятия материалом в школьном курсе алгебры.
Подходы к изучению степенной функции в науке и в школьном курсе математике различны. Существуют различные способы определения степенной функции; наиболее распространенное и наиболее общее из них – аксиоматическое.
Определение. Степенной функцией называется любой непрерывный гамоморфизм группы R в себя, то есть любая функция f, отображающая множество ![]() в себя, обладающая свойствами:
в себя, обладающая свойствами:
1)![]() для всех x, y
для всех x, y![]()
![]()
2) ![]() – непрерывна.
– непрерывна.
Для некоторых значений α степенная функция допускает продолжение на более широкую область определения, чем ![]() . Например, при
. Например, при ![]() на
на ![]() , кроме этого
, кроме этого ![]() ; если же
; если же ![]() , где
, где ![]() , то только на
, то только на ![]() .
.
При α>0 можно доказать, что lim![]() =0 при
=0 при ![]() , поэтому, чтобы не нарушалась непрерывность функции
, поэтому, чтобы не нарушалась непрерывность функции ![]() , и в этомслучае полагают, что
, и в этомслучае полагают, что ![]() .
.
При нечетном ![]() и
и ![]() функция
функция ![]() допускает естественное продолжение на всю числовую прямую; при четном n – это невозможно.
допускает естественное продолжение на всю числовую прямую; при четном n – это невозможно.
Равенство 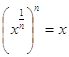 по сути задает функцию
по сути задает функцию![]() как функцию, обратную функции
как функцию, обратную функции ![]() , поэтому функцию
, поэтому функцию ![]() , например, можно считать определенной для всех
, например, можно считать определенной для всех ![]() , а функцию
, а функцию ![]() только для неотрицательных
только для неотрицательных ![]() .
.
В общем виде на ![]() не накладывается никакие условия, поэтому функция
не накладывается никакие условия, поэтому функция ![]() считается определенной на множестве
считается определенной на множестве ![]() .
.
При изучении степенной функции в школьном курсе математики подходят совсем с других позиций: постепенно расширяются значения числа ![]() , причем рассматриваются не функции, например,
, причем рассматриваются не функции, например, ![]() ,
, ![]() , а вводится понятие степени определенного вида.
, а вводится понятие степени определенного вида.
Получаем следующую последовательность: степень с натуральным показателем (7 класс) – степень с нулевым и целым отрицательным показателем (7 класс) – степень с рациональным нецелым показателем (11 класс) – степень с иррациональным показателем (11 класс).
Основным мотивом введения показателей является выполнение свойств степеней.
![]()
![]()
![]()
![]()
![]()
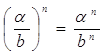 ,
, ![]() .
.
Такое расмотрение приводит к ограничениям на ![]() и
и ![]() . Подход достаточно естественный и мотивированный, но только до момента рассмотрения степени с рациональным показателем.
. Подход достаточно естественный и мотивированный, но только до момента рассмотрения степени с рациональным показателем.
Введению степени с рациональным показателем в школьном курсе математики предшествует рассмотрение действий с корнями. Уже на этом этапе проявляются разногласия автором различных учебников и учебных пособий по математике. Большинство из них определяют корень n – ой степени из положительного числа ![]() для всех
для всех ![]() (например, «Математика в понятиях, определениях и терминах» из серии «библиотека учителя математики», учебники по математике К.О. Ананченко и др.). Авторы же учебного пособия по алгебре для 11 класса дают следующее определение.
(например, «Математика в понятиях, определениях и терминах» из серии «библиотека учителя математики», учебники по математике К.О. Ананченко и др.). Авторы же учебного пособия по алгебре для 11 класса дают следующее определение.
Пусть k – целое число, n – натуральное число, не равное 1. Степенью положительного числа ![]() с рациональным показателем
с рациональным показателем ![]() называется положительный корень n – ой степени из числа
называется положительный корень n – ой степени из числа ![]() .
.
![]() .
.
Такие разногласия вряд ли желательны, поэтому учителю приходится объяснять, что при n=1 получаем равенство.!!!!!
Некоторые задания авторов данного учебного пособия сформулированы, с нашей точки зрения, некорректно. Например, задание 1.134: Запишите корни в виде степени с рациональным показателем: ![]()
![]() ,
, ![]() ,
, ![]() .
.
Выполнить это задание можно только для первого примера, во всех остальных случаях выражения имеют смысл при всех значениях переменных (в последнем примере ![]() ), переход от корней к степеням с рациональным показателем сужает область значений, при которых выражения имеют смысл.
), переход от корней к степеням с рациональным показателем сужает область значений, при которых выражения имеют смысл.
Невозможно выполнить и упражнение 1.138.
Вычислите 8) ![]() , так как выражение
, так как выражение![]() не имеет смысла.
не имеет смысла.
Возникает также правомерный вопрос: почему степень с рациональным нецелым показателем определяется только для положительного числа ![]() . Возникает мысль, что можно было бы разделить рациональные не целые показатели
. Возникает мысль, что можно было бы разделить рациональные не целые показатели ![]() на две группы: p – целое число, q – натуральное нечетное число и вторая группа – p – целое число, q – натуральное нечетное число, и получить различные ограничения на переменную
на две группы: p – целое число, q – натуральное нечетное число и вторая группа – p – целое число, q – натуральное нечетное число, и получить различные ограничения на переменную ![]() , например,
, например, ![]() , где
, где ![]() , но
, но ![]() , где не понятно, почему
, где не понятно, почему ![]() .
.
Учащимся можно пояснить, что без ограничения ![]() невозможно бы провести цепочку преобразований, например, следующих:
невозможно бы провести цепочку преобразований, например, следующих: ![]() .
.
Такие пояснения делают для учащихся более понятным, почему при рассмотрении степени с рациональным нецелым показателем основание должно быть положительным, и при каком показателе основание может быть равным нулю. Хорошо бы также привести и графическую иллюстрацию, показать, что область определения функции ![]() – вся числовая прямая, область определения функции
– вся числовая прямая, область определения функции ![]() – множество неотрицательных чисел.
– множество неотрицательных чисел.
После этого целесообразно выполнить упражнение 1.137. Имеет ли смысл выражение: ![]() ,
, ![]() ,
, ![]() ,
, ![]() и так далее.
и так далее.
Полезно использовать при доказательстве свойств степени с рациональным показателем таблицу «Степени и корни» авторов М.Г. Шраера, В.С. Дувановой «Таблицы по алгебре и началам анализа, 11 классс». Для удобства ссылок в таблице слева помещены свойства арифметических корней, что делает доказательство для учащихся более простым.
Заметим, что свойство 6 степеней с рациональным показателем (при![]() ,
, ![]() , при r>0;
, при r>0; ![]() при r<0) можно в дальнейшем трактовать как возрастание степенной функции
при r<0) можно в дальнейшем трактовать как возрастание степенной функции ![]() на промежутке
на промежутке ![]() при r>0 и ее убывание на этом же промежутке при r<0.
при r>0 и ее убывание на этом же промежутке при r<0.
Таким образом, подводя итоги можно отметить, что изучение степенной функции – одна из наиболее сложных проблем в дидактике математики.
При построении методики изучения вопросов, связанных со степенной функцией целесообразно направлять учебную деятельность на освоение общих способов действий.
Необходимо выявлять происхождение вводимых понятий с точки зрения теоретического познания основ математики.
Изучение учебного материала полезно выстроить по принципу содержательного обобщения, при этом с самого начала формировать учебную деятельность как научно-теоретическую.
3. Практическая часть
3.1 Урок по теме «Показательная функция»
Тема урока: «Степень с действительным показателем. Показательная функция.»
Продолжительность: 45 минут.
Тип урока: лекция.
Цели урока:
1. Образовательная: ввести понятие показательной функции, рассмотреть ее свойства и построить график. Применить изученные свойства показательной функции в решении конкретных заданий и упражнений.
2. Развивающая: совершенствовать умения сравнивать, анализировать, обобщать, развивать навыки компьютерной обработки информации с помощью электронных таблиц.
3. Воспитательная: воспитывать информационную культуру и культуру общения, готовить обучающихся к жизни в современном информационном обществе.
Структура урока:
1. Организационный момент.
2. Актуализация опорных знаний.
3. Изучение нового материала.
4. Первичное закрепление нового материала.
5. Домашнее задание.
Ход урока.
| 1. | Организационный момент. Учитель: (Организует внимание учащихся, предлагает присесть). Здравствуйте, присаживайтесь. | Учащийся присаживаются за парты, в классе устанавливается рабочая атмосфера. |
| 2–3. | Актуализация опорных знаний и изучение нового материала. Учитель: Нам уже известно, что такое степень с рациональным показателем. Теперь определим степень с иррациональным показателем при основании а>0. Пусть s-иррациональное число. Возьмем такие числа r и t, что Опр. Пусть а>0. Степенью числа a с иррациональным показателем s называется такое число b, что Аналогично доказывается и для положительного числа а<0. Опр. Пусть Теорема. Для любых значений
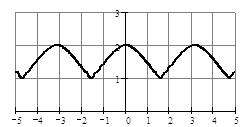
Пример: Расставить числа в порядке убывания чисел: Решение: Сравним числа 3, 3.5, Показательная функция: Рассмотрим выражение Опр. Показательной называется функция вида Область определения показательной функции – это натуральное множество определения выражения На рисунке 1 показан график функции с основанием
На рисунке 1 показан график функции с основанием
Теорема (о свойствах показательной функции Свойства показательной функции: 1. Область определения функции − вся числовая прямая. 2. Область значений функции − промежуток (0;+ 3. Показательная функция наименьшего и наибольшего значения не имеет. 4. График показательной функции пересекается с осью ординат в точке (0; 1) и не пересекается с осью обсцисс. 5. Показательная функция не имеет нулей функции. 6. Показательная функция принимает положительные значениях на всей числовой прямой; все точки ее графика находятся выше оси Ох в I и II координатных углах. 7. Показательная функция не является ни четной ни нечетной. 8. При 9. Показательная функция не является переодической. Данные свойства показательной функции примем без доказательства, график функции позволяет наглядно доказать некоторые свойства. Пример 1: Записать наибольшее и наименьшее значение функции (если они существуют): a) Решение: а) т.к. 3 >0 и 3>1, то большему значению показателя б) т.к. 0<0,7<1, то большему значению показателя sin x соответствует меньшее значение степени
| Определения и все свойства учащиеся записывают в тетради, а остальной материал, излагаемый учителем, слушают и запоминают. За материалом можно следить в учебнике. Учитель: Объясняет, что любой график показательной функции проходит через точку (0; 1). Построение графиков функции происходит по табличному (по точечному) способу. |
| 4. | Первичное закрепление нового материала. 2.10. Является ли показательной функцией (устно): 1. 2. 3. 2.12 Схематически изобразите график функции: 1. 3. 4. | При выполнении упражнений если возникает трудность, то учитель объясняет сложности в выполнении задания. В 2.12 главное в выполнении это определение показательной функции. |
| 5. | Домашнее задание: Домашнее задание включает в себя задания из тех упражнений, которые выполнялись в классе. Также учащимся необходимо усвоить новый материал про показательную функцию. |
3.2 Урок закрепления изученного материла на тему «Показательная функция»
Урок 2. Показательная функция её свойства и график
Продолжительность: 45 минут.
Тип урока: лекция.
Цели урока:
1. Образовательная: обучить основным свойствам показательной функции и графика функции ![]() .
.
2. Развивающая: совершенствовать умения сравнивать, анализировать, обобщать, развивать навыки компьютерной обработки информации с помощью электронных таблиц.
3. Воспитательная: воспитывать информационную культуру и культуру общения, готовить обучающихся к жизни в современном информационном обществе.
Структура урока:
6. Организационный момент.
7. Актуализация опорных знаний и проверка домашнего задания.
8. Закрепление изученного материала.
9. Домашнее задание.
Ход урока:
1. Первый этап: Организационный момент.
Учитель организует внимание и предлагает присесть.
2. Второй этап. Актуализация опорных знаний и проверка домашнего задания.
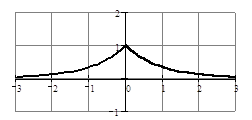
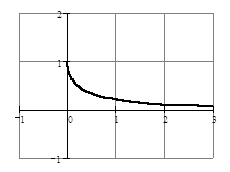
Двое учащихся описывают свойства показательной функции по графикам, построенным на доске.
| График показательной функции | |
|
|
|
|
|
|
Пока учащиеся работают у доски, учитель с остальными учениками отвечают на вопросы:
1) функцию какого вида называют показательной;
2) какова область определения показательной функции;
3) каково множество значений показательной функции;
4) что можно сказать о монотонности показательной функции в зависимости от основания а;
5) Область определения функции:
1. у = ![]() 2. у =
2. у = ![]() 3.у =
3.у = ![]() 4. у =
4. у = ![]() .
.
На заранее подготовленных листах, изображены графики функций. Указать область определения и область значений функций (можно в виде карточек раздать нескольким ученикам и добавить задания, например все свойства данных функций).
|
|
|
|
|
| ||
|
|
|
|
|
|
Проверяется работа учеников у доски и исправляются ошибки, если они есть.
Похожие работы
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...
... материал, который их интересует, повторять материал столько раз, сколько им нужно, и это помогает устранить многие препятствия их индивидуальному восприятию. Использование информационно-коммуникационных технологий при изучении темы «Показательная функция». В настоящее время разработана компьютерная поддержка курса любого предмета, в том числе и математики. Не подменяя собой, учебник или другие ...
... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...
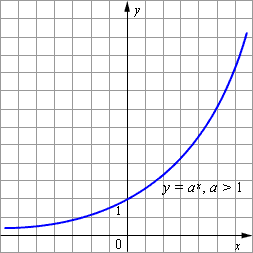 рис. 1.
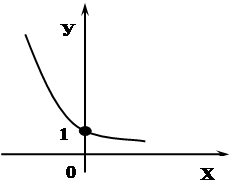
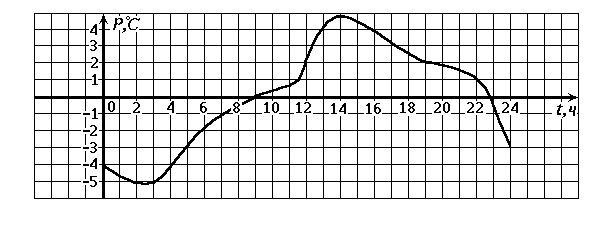
рис. 1. рис. 2.
рис. 2.

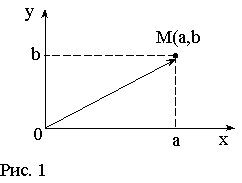
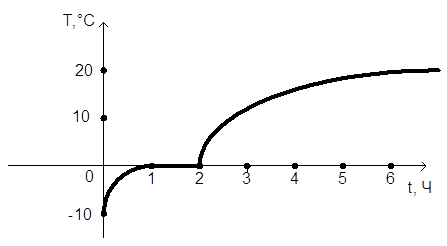
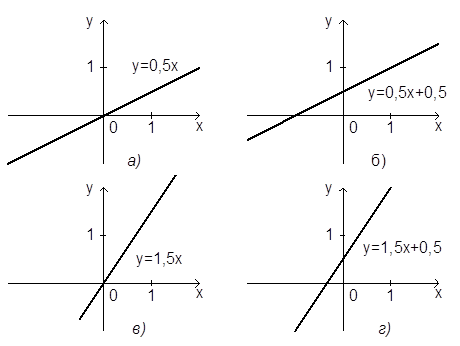
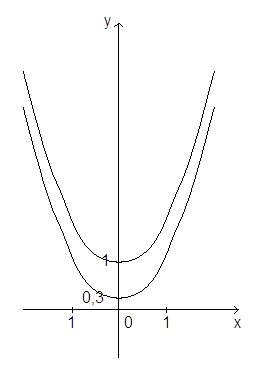
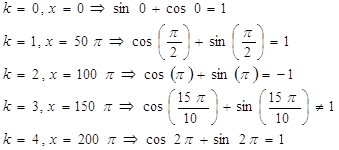
0 комментариев