Навигация
Контрольное исследование качества умений и навыков учащихся в решении составных задач
3.4 Контрольное исследование качества умений и навыков учащихся в решении составных задач
Задачи контрольного эксперимента:
- Выяснить с помощью срезовой контрольной работы уровень умения решать составные задачи каждого ученика;
- Выяснить с помощью контрольной работы умение детей преобразовывать задачи;
По окончании формирующего эксперимента нами были проведены ещё 3 контрольных работы.
Контрольная работа №3.
Итоговая контрольная работа создавалась по типу первой стартовой контрольной работы. Все задания и типы задач остались те же, изменилась лишь сюжетная сторона задач.
Результаты выполнения контрольных работ представлены в Приложении 11.
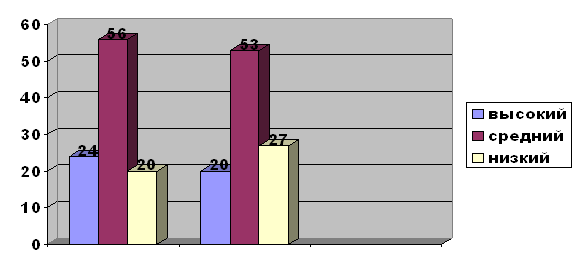
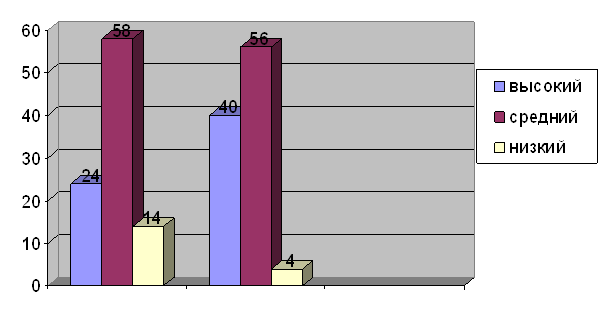
Анализ работ дал следующие результаты: 1 человек остался на низком уровне, 3 человека – на среднем и 14 человек – на высшем. Наглядно это можно увидеть на графике (Приложение11).
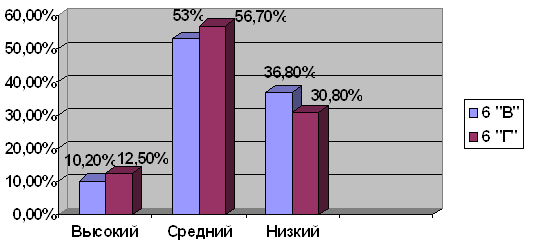
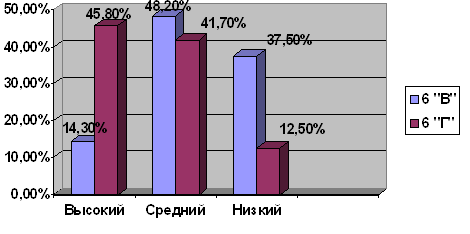
Сравним результаты стартовой и итоговой контрольных работ на едином графике (Приложение 12). При сопоставлении результатов мы видим, что до начала эксперимента все показатели были значительно ниже, но после целенаправленного обучения преобразованию задач результаты заметно улучшились. Исходя из полученных результатов, можно утверждать, что дети лучше стали решать составные задачи.
Контрольная работа №4.
Цель данной контрольной работы выяснить, повысилось ли умение учащихся преобразовывать задачи после проведения данного эксперимента. По сравнению с контрольной работой №2 эта контрольная работа имеет большее количество заданий: здесь предлагается решить две составные задачи и в одной из них изменить условие, а в другой – требование.
Результаты показали, что все учащиеся безошибочно решили обе составные задачи, но с заданием на преобразование условия и требования справились только 14 человек.
Если сравнить полученные данные с контрольной работой №2, то можно увидеть, что решать составные задачи учащиеся стали лучше, количество человек справившихся с заданием на преобразование возросло.
Контрольная работа №5.
Последняя контрольная работа проводилась с целью определить, насколько дети усвоили понятие «преобразовать задачу».
Учащимся было предложено задание: преобразовать задачу, а затем решить преобразованную задачу. Особенность этого задания в том, что учащийся самостоятельно выбирает, что он будет преобразовывать: условие, требование или условие и требование. Таким образом, 16 учащихся справились с заданием, правильно преобразовав и решив задачу.
3.5 Интерпретация и анализ полученных результатов
Сопоставительный анализ полученных данных по итогам написания контрольных работ позволяет сделать вывод о том, что уровень умений решать составную задачу в исследуемом нами классе стал выше, мыслительные операции детей в процессе решения задач стали более осознанными и обоснованными. Подтверждением тому стала таблица сравнения уровней умения решать составные задачи (см. Приложение 12).
Таким образом, подведя итоги нашего исследования, имеет смысл отметить следующее. Результаты проведенного нами исследования доказывают истинность высказанной нами гипотезы: если на уроках математики в начальной школе вести работу по обучению преобразованию задач, то это будет эффективным средством повышения уровня умения решать задачи.
Преобразуя составные задачи, учащиеся уделяют много внимания связи между данными и искомым, что помогает школьнику осознать приемы получения новых задач и постепенно снимает трудности в решении каждой новой задачи.
Заключение
При написании данной курсовой работы перед нами была поставлена цель: изучить специфические особенности и пути усовершенствования процесса обучения школьников решению составных задач.
Для реализации заданной цели в соответствии с поставленными задачами на основе анализа психолого-педагогической и методической литературы по был выявлен понятийный аппарат исследуемой проблеме, систематизирован теоретический материал по работе над составной задачей, а также приемы работы над составной задачей, учитывая опыт учителей начальной школы. Составление, проведение и анализ диагностических данных по исследуемой проблеме являлось решением последней поставленной нами задачей. Таким образом, необходимо сказать, что цель курсовой работы достигнута, поставленные задачи решены.
Итак, в данной курсовой работе исследовалась методика решения составных задач. В результате проведенного исследования можно сделать следующие выводы.
У всех авторов определение задачи сформулировано по-разному, но все авторы сходятся в том, что у решателя должна быть определенная цель, стремление получить ответ на вопрос, в задаче есть условие и требование, необходимые для решения задачи. Условие задачи составляют объекты задачи и отношения между ними. Анализ условия подводит к пониманию известных и к поискам неизвестного. Этот поиск идет в процессе решения задачи. Детям надо объяснить, что решать задачу - это значит понять и рассказать, какие действия нужно выполнить над данными в ней числами, чтобы получить ответ. В тексте задачи указываются связи между данными числами, а также между данными и искомыми. Эти связи и определяют выбор арифметического действия. Все арифметические задачи по числу действий, выполняемых для их решения, делятся на простые и составные.
Решение задач разными способами, получение из нее новых, более сложных задач и их решение в сравнении с решением исходной задачи создает предпосылки для формирования у ученика умения находить свой «оригинальный» способ решения задачи, воспитывает стремление вести «самостоятельно поиск решения новой задачи», той, которая раньше ему не встречалась.
Методика работы над задачей подразумевает несколько этапов. Мы изучали этап работы над задачей после ее решения, на котором одним из видов деятельности является преобразование задач. Используемая нами методика обучения преобразованию задач состоит из трех этапов: подготовительная работа, обучение и закрепление. Мы провели 8 уроков, на которых велась работа по данному направлению. В результате проведенных уроков и последующих контрольных работ мы выяснили, что методика действует, подтверждая выдвинутую нами гипотезу.
Результаты проведенного эксперимента показывают, что обучение с применением метода преобразования задач повышает активность мыслительной деятельности учащихся, помогает понять задачу, осознать выбор действия, найти самостоятельно рациональный путь решения, установить нужный способ проверки, определить условия, при которых задача имеет или не имеет решения.
Исследования доказали, что если на уроках математики в начальной школе вести работу по обучению преобразованию задач, то это будет эффективным средством повышения общего уровня умения решать составные задачи.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Алмазова, И.Р. Сборник задач и примеров по математике для начальных классов / И.Р. Алмазова. – М.: Просвещение, 2003. – 170с.
Белошистая, А. В. Методика преподавания математики в начальной школе / А.В. Белошистая. – М.: Владос, 2005. – 455с.
Белошистая, А.В. Прием графического моделирования при обучении решению задач / А.В. Белошистая // Начальная школа. – 2006. – №8. – С. 36–39.
Волкова, С.И. Карточки с математическими заданиями 4 кл. / С.И. Волкова. – М.: Просвещение, 1993. – 207с.
Далингер, В.А. Методика реализации внутрипредметных связей при обучении математике / В.А. Далингер. – М.: Просвещение, 1991. – 149с.
Демидова, А.Е. Обучение решению некоторых видов составных задач / А.Е. Демидова // Начальная школа: плюс до и после. – 2003. –№4. – С.34–37.
Жиколкина, Т.К. Математика. Книга для учителя. 2 кл. / Т.К. Жиколкина. – М.: Дрофа, 2000. –213с.
Зайцев, В.В. Математика для младших школьников. Методическое пособие для учителей и родителей/ В.В. Зайцев. –М.: Владос, 1999. – 307с.
Истомина, Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и высш. пед. учеб. заведений / Н.Б. Истомина – М.: Издательский центр "Академия", 2002. – 512с.
Казько, Е.С. Работа над текстом задачи с пропорциональными величинами/ Е.С. Казько // Начальная школа. – 1998. –№5. – С.28–33.
Колоскова О.П. Формирование учебных умений младших школьников в процессе обучения решению текстовых задач / О.П. Колоскова // Начальная школа. – 2008. –№9.– С.29–32.
Лавриненко, Т.А. Как научить детей решать задачи / Т.А. Лавриненко. – Саратов: Лицей, 2000. – 264с.
Мамыкина, М.Ю. Работа над задачей / М.Ю. Мамыкина // Начальная школа. – 2003. – №4. – С.17–21.
Матвеева, А. Н. Использование различного построения моделей в процессе обучения решению текстовых задач / А.Н. Матвеева // Начальная школа: плюс до и после. – 2005. – №9. – С.77–79.
Моршнева, Л.Г. Дидактический материал по математике / Л.Г. Моршнева, З.И. Альхова. – Саратов: Лицей, 1999. – 129с.
Никифорова Е.Ю. Активизация мыслительной деятельности в процессе работы над задачей / Е.Ю. Никифоорова // Начальная школа. – 2008. – №8. – С.45–47
Носова, Е.А. Логика и математика для дошкольников / Е.А. Носова, Р.Л. Непомнящая.– С-П.: Детство Пресс, 2000. – 158с.
Петерсон, Л.Г. Математика 1 класс. Методические рекомендации / Л.Г. Петерсон – М.: Баласс, 2005. – 397с.
Сергеев, И.Н. Примени математику / И.Н. Сергеев, С.Н. Олехин, – М.: Наука, 1991. – 113с.
Скворцова, С.С. Урок на тему «Составные задачи» / С.С. Скворцова // Начальная школа. –2008. – №8. – С.52–54.
Сурикова, С.В. Использование графовых моделей при решении задач / С.В. Сурикова, М.В. Анисимова // Начальная школа. – 2000. – №4. – С.67–74.
Темербекова, А.А. Методика преподавания математики: Учеб. пособие для студ. высш. учеб. Заведений / А.А. Темербекова. – М.: Гуманит. изд. центр ВЛАДОС, 2003. – 490с.
Тонких, А.П. Математика: Учебное пособие для студентов факультетов подготовки учителей нач. кл-в.: В 2-х книгах. Кн. 1. – М.: Книжный дом "Университет", 2002. – 472с.
Узорова, А.И. 3000 задач и примеров по математике / А.И. Узорова. –М.: Просвещение, 1996. – 598с.
Фонин, Д.С. Моделирование как важное средство обучения решению задач / Д.С. Фонин, И.И. Целищева // Начальная школа. – 1990. – №3. –С. 55– 62.
Фридман, Л.М. Методика обучения решению математических задач / Л.М. Фридман // Математика в школе. – 1991.– №5. – С.27–29.
Царева, С.В. Обучение решению задач / С.В. Царева // Начальная школа. – 2000. – №12. – С.64–67.
Целищева, И.И. Использование моделирования в процессе работы с текстовой задачей / И.И. Целищева // Начальная школа. – 2008. – №1. С.55– 62.
Чванов, В. Г. Переформулировка задачи / В.Г. Чванов // Математика в школе. – 1997. – №5. – С.23–27.
Шикова, Р.Н. Использование моделирования в процессе обучения математике / Р.Н. Шикова // Начальная школа. – 2004. – №12. – С.54–58.
Шикова, Р.Н. Методика обучения решению задач, связанных с движением тел / Р.Н. Шикова // Начальная школа. – 2000. – №5. – С.64–69.
Шикова, Р.Н. Решение задач на движение в одном направлении / Р.Н. Шикова // Начальная школа. – 2000. – №12. – С.39–42.
Шилова, О.А. "Симпатичные" задачи / О.А. Шилова // Начальная школа: приложение к газете "Первое сентября".– 2002. – №3. – С.18–19.
ПРИЛОЖЕНИЯ
Приложение 1
Памятка работы над задачей
1. Читай задачу и представляй себе то, о чем говорится в задаче.
2. Запиши задачу кратко или выполни чертеж.
3. Объясни, что показывает каждое число, и назови вопрос задачи.
4. Подумай, какое число получится в ответе: большее или меньшее, чем данные числа.
5. Подумай, можно ли сразу ответить на вопрос задачи, если нет, то почему? Что можно узнать сначала, что потом?
6. Составь план решения задачи.
7. Выполни решение.
8. Ответь на вопрос задачи.
9. Проверь решение.
Приложение 2
Классификация задач на нахождение четвертого пропорционального
| № вида задачи | Величины | ||
| 1-я величина (например - цена) | 2-я величина (например - количество) | 3-я величина (например - стоимость) | |
| 1 | Постоянная | Даны два значения | Дано одно значение, а другое является искомым |
| 2 | Постоянная | Дано одно значение, а другое является искомым | Даны два значения |
| 3 | Даны два значения | Постоянная | Дано одно значение, а другое является искомым |
| 4 | Дано одно значение, а другое является искомым | Постоянная | Даны два значения |
| 5 | Даны два значения | Дано одно значение, а другое является искомым | Постоянная |
| 6 | Дано одно значение, а другое является искомым | Даны два значения | Постоянная |
Приложение 3
Таблицы для решения задач на нахождение четвертого пропорционального
| № вида задачи | Величины | ||
| 1-я величина (например - цена) | 2-я величина (например - количество) | 3-я величина (например - стоимость) | |
| 1 | Одинакова | А | С |
| В | ? | ||
| 2 | Одинакова | С | А |
| ? | В | ||
| 3 | А | Одинакова | С |
| В | ? | ||
| 4 | С | Одинакова | А |
| ? | В | ||
| 5 | А | С | Одинакова |
| В | ? | ||
| 6 | С | А | Одинакова |
| ? | В | ||
Приложение 4
Конспект урока математики для 3 класса по теме:
«Решение задач на нахождение четвертого пропорционального»
Задачи урока:
Обучающие:
познакомить детей с новым видом задач на нахождение четвертого пропорционального;
показать приемы кратного сравнения чисел;
совершенствовать навыки решения задач.
Воспитывающие:
воспитывать интерес к математике.
воспитывать самостоятельность, аккуратность в ведении рабочих тетрадей.
Развивающие:
развивать внимание, логическое мышление, математическую речь.
План работы:
1. Организационный момент.
2. Устный счёт.
Игра «Цепочка».
Игра «День - ночь».
3. Актуализация познавательной деятельности.
4. Работа по новой теме.
Введение новой темы.
Первичное закрепление.
Физкультминутка.
Закрепление.
5.Итог урока.
6.Домашнее задание.
Ход урока:
1. Организационный момент.
- Здравствуйте, дети! Сегодня мы с вами продолжаем закреплять таблицу умножения на 2, на 3, на 4, на 5, на 6, а также мы сегодня познакомимся с новым видом решения задач.
2. Устный счет.
Игра «Цепочка».
Учитель задает примеры, совершая действия с предыдущим ответом:
1. 56 – 32 = 24
2. 24 : 6 = 4
3. 4 * 4 = 16
4. 16 : 2 = 8
5. 8 + 32 = 40
6. 40 : 10 = 4
7. 4 + 37 = 41
8. 41 – 11 = 30
9. 30 : 3 = 10
10. 10 + 26 = 36
11. 36 : 9 = 4
12. 4 * 7 = 28
13. 28 - 14 = 14
14. 14 : 7 = 2
15. 2 * 0 = 0
16. 0 + 55 = 55
17. 55 - 33 = 22
18. 22 – 4 = 18
19. 18 : 9 = 2
20. 2 + 18 = 20
21. 20 : 2 = 10
22. 10 * 4 = 40
23. 40 - 17 = 23
24. 23 + 7= 30
25. 30 + 45 = 75
26. 75 + 25 = 100
Игра «День – ночь».
Когда учитель говорит “ночь”, учащиеся закрывают глаза. В уме они должны решить цепочку примеров, например: 20+26-30-8+7+15+50-14+9=? А когда учитель говорит “день”, ученики открывают глаза, те которые решили, поднимают руки.
27 + 9 : 4 + 6 : 5 * 7 + 19 : 10 = 4
Продолжение приложения 4
45 : 5 – 3 * 6 : 4 * 5 -20 = 20
54 : 9 * 5 – 15 : 5 * 9 = 27
60 : 6 + 14 : 6 * 8 + 4 : 6 = 6
32 : 8 * 4 : 2 * 6 – 3 : 5 = 9
5 * 7 – 5 : 6 * 5 – 1 : 4 * 7 = 42
3. Актуализация познавательной деятельности.
- Открыли свои учебники на странице 64 № 3 выполняем устно.
Таким образом, уменьшить в несколько раз – разделить; увеличить в несколько раз – умножить; уменьшить на несколько единиц – вычесть; увеличить на несколько единиц – сложить.
- Сейчас посмотрите на № 4. В этом номере даны два отрезка. Измерьте длины этих отрезков.
- Какой длины получились отрезки? (АВ = 3 см, МК = 9 см)
- Во сколько раз отрезок АВ короче отрезка МК? (В 3 раза)
- Как мы это узнали? (9 : 3)
- Откройте страницу 62 и прочитайте правило.
- А теперь скажите на сколько один отрезок длиннее другого? (На 6 см)
- Как вы это узнали? (6 – 3)
- Запишите задачу в тетрадь.
Похожие работы
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...
... системы развивающего обучения - свойства вариантности, учитывающего прежде всего индивидуальные особенности школьников. самоконтроль школьник тестовый орфографический Глава 3. Опытно-экспериментальная работа по формированию навыков орфографического самоконтроля у младших школьников на уроках русского языка Опытно-экспериментальная работа по проверке теоретически выделенных методов и ...
... задача: «Туристы шли с одинаковой скоростью и за 2 дня прошли расстояние 36 км. В первый день они были в пути 4ч, а во второй – 5ч. С какой скоростью шли туристы?» При решении задач на движение в качестве средств наглядности, как правило, используются схематические чертежи. Однако в некоторых задачах на чертеже не всегда удается показать все величины и связи между ними, а также обозначить вопрос. ...
... нового и сложного типа проблем или когда надо осветить проблему, самостоятельное решение которой учащимся недоступно. 1.2 Психологические основы исследовательского обучения школьников К фундаментальным идеям, на которых строится исследовательское обучение, могут быть отнесены следующие принципы. Принцип ориентации на познавательные интересы учащегося. Исследование – процесс творческий, ...
0 комментариев