Организация процесса повторения в курсе геометрии 7-9 классов

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет

Математический факультет

Кафедра математического анализа и МПМ

Выпускная квалификационная работа

Организация процесса повторения в курсе геометрии 7-9 классов

Выполнила:

студентка V курса математического факультета

Шестакова Ирина Валерьевна

Научный руководитель:

кандидат педагогических наук, доцент кафедры математического анализа и МПМ И.В. Ситникова

Рецензент:

кандидат педагогических наук З.В. Шилова

Допущена к защите в государственной аттестационной комиссии

«___» __________2005 г. Зав. кафедрой М.В. Крутихина

«___»___________2005 г. Декан факультета В.И. Варанкина

Киров

2005

Содержание

Введение. 3

§1 Требования к организации повторения. 6

§2 Виды повторения. 10

2.1. Повторение пройденного в начале года. 10

2.2. Текущее повторение ранее пройденного. 12

2.3. Тематическое повторение. 15

2.4. Заключительное повторение. 19

2.5. Классификация повторения в зависимости от содержания повторяемого материала 24

§3 Подготовка учителя к урокам повторения. 28

§4 Методы, формы и средства повторения. 34

Заключение. 53

Библиографический список. 54

Приложение. 56

Введение

В процессе обучения математике повторению изученного материала отводится важное место. Правильно организованное повторение – один из факторов, способствующих интеллектуальному развитию каждого школьника, достижению им глубоких и прочных знаний. Без сохранения приобретенных знаний, без умения применить пройденный материал в необходимый момент - изучение нового материала всегда сопряжено с большими трудностями и не дает надлежащего эффекта. Таким образом, цель повторения – установить логические связи между вновь изучаемым и ранее изученным материалом, обогатить память, расширить кругозор, привести знания в систему, самоорганизовать ученика.

Необходимость повторения обусловлена задачами обучения, требующими прочного и сознательного овладения им.

Указывая на важность процесса повторения учебного материала, современные исследователи показали значительную роль при этом таких дидактических приемов, как сравнение, классификация, анализ, синтез, обобщение, содействующих интенсивному протеканию процесса запоминания. При этом вырабатываются гибкость, подвижность ума, обобщенность знаний.

В процессе повторения память у учащихся развивается. Эмоциональная память, опирающаяся на наглядно-образные процессы, постепенно уступает памяти с логическими процессами мышления, которая основана на умении устанавливать связи между известными и неизвестными компонентами, сопоставлять абстрактный материал, классифицировать его, обосновывать свои высказывания.

Повторение учебного материала по математике осуществляется во время всего учебного процесса: при изложении учителем новых понятий, при закреплении изученного ранее, при организации самостоятельных работ различных видов, при проверке знаний учащихся и т. д.

Необходимость повторения изученного ранее материала вызвана самой структурой программы учебного курса математики. Изучение некоторых вопросов школьного курса математики осуществляется постепенно, а развитие ее основных идей продолжается на протяжении всего периода обучения в школе, и вследствие этого учащиеся в подавляющем большинстве своем недостаточно видят эти идеи, являющиеся остовом, на котором закрепляются все другие вопросы курса. Поэтому возникает необходимость работы над ведущими идеями, что успешно осуществляется при повторении.

В процессе изучения геометрии повторение имеет особое значение. Специфика предмета повторения состоит в том, что материал каждого урока логически связан с ранее пройденным, иногда далеко отстоящим по времени от изучаемого. Ученик лишь в том случае станет активным участником учебного процесса, если при получении новых знаний у него будет иметься соответствующая база знаний. Ее наличие во многом определяется систематическим и правильно организованным повторением.

Однако повторению в курсе геометрии 7-9 класс уделяется мало внимания.

В связи с этим особо важное значение для организации успешного обучения учащихся геометрии имеет систематическое повторение ранее изученного, связанного с данным уроком, с материалом предшествующих лет, т. е. систематическое возвращение к ранее изученному.

Таким образом, актуальность темы работы обусловлена:

-     необходимостью развития творческого мышления учащихся и обучения основным методам научного познания: обобщению, конкретизации, аналогии и т. д.;

-     отсутствием достаточно-разработанной методики организации повторения в курсе геометрии 7-9 класс;

-     недостаточным умением учащихся самостоятельно систематизировать знания, полученные в разное время, пользоваться ими при необходимости;

-     недооценкой роли повторения в процессе обучения.

Объект исследования: процесс изучения геометрии в 7-9 классах.

Предмет исследования: организация повторения при изучении геометрии в 7-9 классах.

Цель работы: изучить цели и возможности организации повторения в курсе геометрии 7-9 классов.

Поставленная цель определила следующие задачи исследования:

1.    изучить учебно-методическую и психолого-педагогическую литературу по теме исследования;

2.    определить требования к организации повторения;

3.    рассмотреть различные подходы к классификации видов повторения;

4.    выделить основные формы и методы повторения;

5.    перечислить требования к подготовке уроков повторения.

Гипотеза исследования: систематическая организация повторения при изучении геометрии в 7-9 классах, в соответствии с выделенными требованиями, видами и формами будет способствовать более прочному усвоению материала, его обогащению и расширению.

§1 Требования к организации повторения

Чтобы обеспечить прочность знаний и навыков, приобретаемых учащимися в процессе изучения математики, нужно правильно организовать повторение, т. е. возвращение к уже пройденному материалу, преследуя две цели, а именно: окончательную доработку программного материала, его, так сказать, отшлифовку, и вместе с тем его закрепление в памяти учащихся.

Цели и время повторения тесно связаны и взаимообусловлены и в свою очередь определяют методы и приемы повторения.

Поэтому задачи повторения и методика его проведения могут быть выражены в трех следующих вопросах, по существу исчерпывающих смысл повторения: Что повторять? Как повторять? Когда повторять?

Первый из этих вопросов касается выбора материала для повторения, второй имеет в виду систему и методы повторения, а третий вопрос тесно связан с организацией педагогического процесса.

При планировании повторения необходимо отобрать материал, установить последовательность и время повторения, распределить отобранный материал по урокам, установить формы и методы для осуществления повторения, разумеется, надо учитывать и свойства памяти.

Основные требования к организации повторения должны исходить из целей повторения, специфики математики как учебного предмета, ее методов.

Первое требование к организации повторения, исходящее из его целей, это определение времени: Когда повторять? Самый общий ответ на поставленный вопрос таков: повторение следует проводить в течение всего учебного года. Оно должно осуществляться по принципу: «Учить новое, повторяя, и повторять, изучая новое» (В. П. Вахтеров) [3].

Это не означает, однако, что нельзя специально отводить уроки для повторения, скажем, для таких вопросов программы, которые трудно усваиваются и которые вместе с тем не всегда удается увязать с текущим материалом.

План повторения и выбор тем для повторения учитель должен составлять в каждом отдельном случае на основании общих теоретических соображений с учетом того, как усвоен учащимися материал соответствующих разделов.

К сказанному добавим еще то, что характер урока математики в связи с переходом учащихся из одного класса в другой значительно меняется.

В старших классах существенно перестраивается закрепление и повторение учебного материала. Увеличивается объем фактического материала, выносимого на закрепление и повторение; поурочное закрепление в ряде случаев переходит в тематическое или перерастает в обобщающее повторение, увеличивается доля самостоятельности учащихся при закреплении и повторении.

Второе требование к организации повторения должно отвечать на вопрос: Что повторять? Исходя из высказываний классиков педагогики, положительного опыта дореволюционной и советской школ, можно выдвинуть следующие положения при отборе учебного материала по различным видам повторения:

1.    Не следует повторять все, ранее пройденное. Нужно выбрать для повторения наиболее важные вопросы и понятия, вокруг которых группируется учебный материал.

2.    Выделять для повторения такие темы и вопросы, которые по трудности своей недостаточно прочно усваиваются.

3.    Выделять для повторения надо то, что необходимо обобщить, углубить и систематизировать.

4.    Не следует повторять все в одинаковой степени. Повторять основательно надо главное и трудное. При отборе материала для повторения необходимо учитывать степень его связи с вновь изучаемым материалом. [3]

Третье требование к организации повторения математики должно отвечать на вопрос, как повторять, т. е. осветить те методы и приемы, которыми должно осуществляться повторение. Методы и приемы повторения должны находиться в тесной связи с видами повторения.

При повторении необходимо применять различные приемы и методы, сделать повторение интересным, путем внесения? как в повторяемый материал, так и в методы изучения некоторых элементов новизны.

По поводу полезности многообразия методов и приемов весьма удачно выразился немецкий математик-педагог Керр: «Лучше одну теорему разобрать десятью способами, чем десять теорем одним способом» [3]. К сожалению, этому хорошему принципу следуют далеко еще не все преподаватели математики.

Только разнообразием методов повторения можно устранить то противоречие, которое возникает, с одной стороны, ввиду отсутствия желания у части учащихся повторять то, что ими усвоено однажды, а с другой — в силу необходимости повторять с целью углубления, обобщения и систематизации ранее изученного материала.

Для успешности повторения необходимо соблюдать следующие условия:

1.    Повторять надо в течение всего учебного года, т. е. чтобы повторение не было работой от случая к случаю, чтобы повторение входило органической частью в саму методику изучения математики.

2.    Должна быть четкая целеустремленность в работе, сознательное отношение учащихся к повторению, осознание ими задач и результатов, которых они должны добиться при повторении.

3.    Тщательно отбирать материал и продумывать планирование его при повторении.

4.    Стимулировать самостоятельность и активность в процессе повторения, что достигается разнообразием форм и. методов повторения.

5.    Правильно дозировать и распределять материал повторения во времени.

6.    Соблюдать установку: «Учить, чтобы усвоить и запомнить».

Без целевой установки даже многократное повторение может не дать желаемого результата.

7.    Органически связывать и продумывать сочетание отдельных видов повторения. Основные виды повторения должны дополнять друг друга, представлять стройную систему педагогически целесообразного повторения.

Работа на уроках повторения и на уроках первичного усвоения различна. Это объясняется своеобразием работы ученика по усвоению нового материала от работы при повторении пройденного, усвоенного уже однажды. Повторением, которое должно помочь учителю в приведении в систему знаний и умений учащихся, мы должны:

а)    устранить недочеты в знаниях учащихся;

б)    углубить и расширить знания учащихся по данному вопросу;

в)    предупредить забывание основного содержания материала;

г)    воспроизвести ранее пройденный материал на более высокой ступени в новых связях и комбинациях;

д)    обобщить, систематизировать и окончательно закрепить наиболее существенное из учебного материала.

При повторении математики значительную часть времени приходится уделять теории, так как у учащихся возникает много вопросов, требующих более полного и глубокого освещения.

8.    Уроки повторения должны быть продуманы как с точки зрения содержания, так и организации их. Постановка самих вопросов и разбор упражнений по своей форме и характеру должны заставлять несколько по-иному осмысливать прежний материал. [3]

Различные виды повторения тесно взаимодействуют; от своевременного и успешного проведения одного из видов повторения, например тематического или текущего, зависит продолжительность и успешность повторения другого вида — заключительного повторения или повторения в конце учебного года. Перейдем к краткой характеристике видов повторения.

§2 Виды повторения.

В существующей методической литературе, в той или иной мере систематизирующей вопросы повторения школьного курса математики, встречается различная терминология при классификации видов повторения.

Наиболее часто встречается следующая классификация видов повторения:

1.    Повторение в начале учебного года.

2.    Текущее повторение всего, ранее пройденного:

а)    повторение пройденного в связи с изучением нового материала (сопутствующее повторение);

б)    повторение пройденного вне связи с новым материалом.

3.    Тематическое повторение (обобщающее и систематизирующее повторение законченных тем и разделов программы).

4.    Заключительное повторение (организуемое при окончании прохождения большого раздела программы или в конце учебного года). [2]

Охарактеризуем более подробно каждый и выделенных видов.

2.1. Повторение пройденного в начале года

При повторении в начале учебного года на первый план должно выдвигаться повторение тем, имеющих прямую связь с новым учебным материалом. Новые знания, приобретаемые на уроке, должны опираться на прочный фундамент уже усвоенных.

При повторении в начале года необходимо наряду с повторением тем, тесно связанных с новым материалом, повторить и другие разделы, которые пока не примыкают к вновь изучаемому материалу. Здесь необходимо сочетать обе задачи: провести общее повторение в порядке обзора основных вопросов из материала прошлых лет и более глубоко повторить вопросы, непосредственно связанные с очередным материалом по программе нового учебного года.

Само повторение следует проводить как в классе, так и дома. При решении вопроса, какой материал должен быть повторен в классе и какой оставлен учащимся для самостоятельного повторения дома, надо исходить из особенностей материала. Наиболее трудный материал повторять в классе, а менее трудный давать на дом для самостоятельной работы.

Например, в IX классе на уроках вводного повторения следует повторить понятия вектора, суммы и разности векторов, произведения вектора на число, их свойства. Полезно также повторить некоторые свойства треугольников и четырехугольников: теорему Пифагора, свойство средней линии треугольника, формулы вычисления площади треугольника, понятия медианы, биссектрисы и высоты треугольника, понятия параллелограмма и трапеции, свойства и признаки параллелограмма, ромба, прямоугольника. Цель этого повторения напомнить учащимся сведения, необходимые для изучения геометрии в IX классе.

Повторение можно организовать в ходе решения следующих задач:

1.    В треугольниках ABC и A_lB_lC_l дано: АВ = А₁В₁ AC = A₁C₁, точки D и D_l лежат соответственно на сторонах ВС и В₁С₁, AD = A₁D_l. Докажите, что данные треугольники равны, если AD и A₁D₁. а) высоты; б) медианы.

2.    Докажите, что центр окружности, вписанной в равнобедренный треугольник, лежит на высоте, проведенной к основанию.

3.    Докажите, что центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к его основанию, или на ее продолжении.

4.    Докажите, что треугольник является равнобедренным, если две его медианы равны.

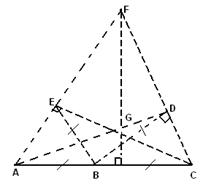
5.    Докажите, что если в треугольнике две высоты равны, то центр вписанной в него окружности лежит на одной из медиан этого треугольника, а центр описанной окружности — на той же медиане или ее продолжении.

6.    Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.

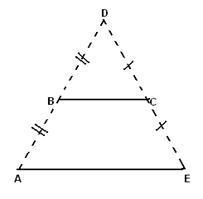
7.    Докажите, что отрезки, соединяющие середины противоположных сторон равнобедренной трапеции, взаимно перпендикулярны.

8.    Найдите длины отрезков, соединяющих середины сторон трапеции с равными диагоналями, если ее основания равны 7 см и 9 см, а высота равна 8 см.

9.    Диагонали параллелограмма ABCD пересекаются в точке М. Упростите выражение: a) ; б) ; в) ; г) ; д) ; e) .

10.  Точка М — середина отрезка АВ, а О — произвольная точка плоскости. Докажите, что .

11.  Точки М и Р — середины диагоналей АС и BD трапеции ABCD с основаниями AD и ВС. Докажите, что .

12.  Даны попарно неколлинеарные векторы ,  и . Постройте векторы: a) ; б) .