Навигация
Содержание внеклассной работы
2.3 Содержание внеклассной работы
Традиционная тематика внеклассных занятий ограничивалась обычно рассмотрением таких вопросов, которые хотя и выходили за рамки официальной программы, но имели много точек соприкосновения с рассматриваемыми в ней вопросами.
Так, например, при изучении в 6 классе признаков делимости натуральных чисел на занятиях математического кружка рассматривались признаки делимости чисел, не предусмотренные программой (признаки делимости на 7, на 11 и т.д.); при изучении геометрических задач на построение циркулем и линейкой на занятиях математического кружка рассматривались геометрические построения при помощи одной линейки и т.п.
Также традиционным для рассмотрения на внеклассных занятиях по математике были исторические экскурсии по той или иной теме, математические софизмы, задачи повышенной трудности и т.д.
За последние десятилетия в математике возникли новые направления, имеющие не только большое практическое значение, но и большой познавательный интерес. Экспериментальные исследования, проведенные в ряде школ, показали, что многие весьма серьезные вопросы математики (в объеме своих начальных понятий) вполне доступны и весьма интересны для изучения их учащимися, даже начиная с 5 класса.
Обновление содержания основного курса математики привело к возникновению тенденции обновления содержания внеклассных занятий по математике, однако, это означает, что следует полностью отказаться от тех или иных традиционных вопросов, которые составляли до сих пор содержание внеклассных занятий и вызывают у учащихся неизменный интерес (например, функции и графики, математические парадоксы и софизмы, неопределенные уравнения, логические и исторические задачи и т.д.).
2.4 Основные формы организации внеклассной работы
Внеклассная работа проводится учителем со своими учениками. Может быть использована одна или несколько конкретных форм: математический кружок; неделя или месячник математики; математические вечера, утренники; различные соревнования, игры, викторины, конкурсы, командные соревнования; школьные олимпиады по математике; школьная и классная математическая печать; клубы веселых математиков; математические экскурсии и кино-экскурсии; внеклассное чтение научно-популярной математической литературы; школьные научные конференции; подготовка учащимися докладов, рефератов и сочинений по математике; изготовление математических моделей и др.
Указанные формы работы часто пересекаются, и поэтому трудно провести между ними резкие границы. Более того, элементы многих форм могут быть использованы при организации работы в основном по какой-либо одной из них. Например, при проведении математического вечера можно использовать соревнования, конкурсы, доклады и т.д.
2.5 Общая характеристика и методика проведения основных форм внеклассной работы
Одной из распространенных форм внеклассной работы является математический кружок. Вопросы организации, содержания и методики его работы достаточно полно освещены в методической литературе. В ней можно найти рекомендации по построению занятий, перечень тематики и библиографию источников, домашние и творческие задания для участников кружка и т.д.
В работе математических кружков можно выделить два направления. Первое в основном ориентированно на развитие мышления и формирование первоначального интереса к математике, второе на углубление знаний по математике и параллельно с этим на дальнейшую работу по развитию мышления.
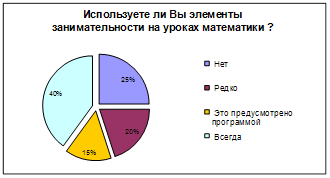
В работе математического кружка большое значение имеет занимательность материала и систематичность его изложения. Занимательность повышает интерес к предмету и способствует осмыслению важной идеи: математика окружает нас, она есть везде. Систематичность изложения материала может быть направлена на общее умственное развитие учащихся.
Каждая из форм внеклассной работы обладает своими особенно ценными качествами. Математические соревнования, например, привлекательны тем, что участвовать в них стремятся почти все ученики. Это учитель может использовать как для повышения интереса к математике, так и для организации коллективной умственной деятельности учеников. Последнее мы считаем, особенно существенным, поскольку в изучении математики потребность в объединении усилий нескольких равноправных участников, встречается нечасто.
Математический кружок – одна из наиболее действенных и эффективных форм внеклассных занятий. В основе кружковой работы лежит принцип строгой добровольности. Обычно кружковые занятия организуются для хорошо успевающих учащихся. Однако следует иметь в виду, что иногда и слабо успевающие учащиеся изъявляют желание участвовать в работе математического кружка и нередко весьма успешно занимаются там; учителю математике не следует этому препятствовать. Необходимо лишь более внимательно отнестись к таким учащимся, постараться укрепить имеющиеся у них ростки интереса к математике, проследить за тем, чтоб работа в математическом кружке оказалась для них посильной. Конечно, наличие слабо успевающих учащихся среди членов математического кружка затрудняет работу учителя, однако путем индивидуализации заданий, предлагаемых учителем кружковцам, можно в некоторой степени ослабить эти трудности. Главное – сохранить массовый характер кружковых занятий по математике, являющийся следствием доступности посещения кружковых занятий всеми желающими.
Уже при организации математического кружка, необходимо заинтересовать учащихся, показать им, что работа в кружке не является дублированием классных занятий, четко сформулировать цели и раскрыть характер предстоящей работы (для этого целесообразно выделить часть времени на одном из уроков математики, с тем, чтобы обратиться с сообщением об организации кружка по всему классу).
На первом занятии кружка надо наметить основное содержание работы, выбрать старосту кружка, договориться с учащимися о правах и обязанностях члена кружка, составить план работы распределить поручения за те или иные мероприятия (выпуск математической стенной газеты, ведение документации работы кружка и т. п.).
Занятия кружка целесообразно проводить один раз в неделю, выделяя на каждое занятие по одному часу. К организации работы математического кружка целесообразно привлекать самих учащихся (поручать им подготовку небольших сообщений по изучаемой теме, подготовку справок исторического характера, изготовление моделей и рисунков к данному занятию и т. д.). На занятиях математического кружка учитель должен создать атмосферу свободного обмена мнениями и активной дискуссии.
Одной из форм организации внеклассной работы являются факультативные занятия. Главной целью факультативных занятий по математике является углубление и расширение знаний, развитие интереса учащихся к предмету, развитие их математических способностей, привитие школьниками интереса и вкуса к самостоятельным занятиям математикой, воспитание и развитие их инициативы и творчества.
Программа факультативных занятий по математике составлена так, что все вопросы ее могут изучаться синхронно с изучением основного курса математики в школе. В тех случаях, когда в данном классе основной курс математики ведет один учитель, а факультатив другой, изучение тем факультатива может проводиться независимо от основного курса программы.
Для того чтобы факультативные занятия по математике были эффективными, необходимо их организовать там, где есть:
высококвалифицированные учителя или другие специалисты, способные вести занятия на высоко научно-методическом уровне;
не менее 15 учащихся, желающих изучать данный факультативный курс.
Проведение факультативных занятий по математике не означает отказа от других форм внеклассной работы (математические кружки, вечера, олимпиады и т.д.). Они должны дополнять эти формы работы с учащимися, которые интересуются математикой.
Возможность 1-2 часа в неделю дополнительно работать со школьниками, проявляющими повышенный интерес к математике, представляет собой одно из проявлений новой формы обучения математике – дифференциального обучения.
По существу факультативные занятия являются наиболее динамичной разновидностью дифференциации обучения.
Факультативные занятия содействуют профессиональной ориентации учащихся в области математики и ее приложений, облегчая тем самым выбор специальности и дальнейшее совершенствование в ней.
Различия в деятельности факультативных занятий и математических классов с тем, что первые не требуют перестройки системы обучения математике. Они работают на базе общего курса математики. Организация факультативных занятий значительно проще, чем математического класса. Поэтому факультативные занятия – более массовая форма повышенной математической подготовки школьников.
Факультативные занятия играют большую роль в совершенствовании школьного, в том числе математического, образования. Они позволяют производить поиск и экспериментальную проверку нового содержания, новых методов обучения.
В какой бы форме, и какими бы методами не проводились факультативные занятия по математике, они должны строиться так, чтобы быть для учащихся интересными, увлекательными, а подчас занимательными. Необходимо использовать естественную любознательность школьника для формирования устойчивого интереса к своему предмету.
Основными формами проведения факультативных занятий по математике являются в настоящее время изложения узловых вопросов данного факультативного курса лекционным методом, семинары, собеседования (дискуссии), решение задач, рефераты учащихся как по теоретическим, так и по решению цикла задач, математические сочинения, доклады учащихся и т.д.
Одной из важных форм ведения факультативных занятий по математике является разделение каждого занятия на две части. Первая часть посвящается изучению нового материала в самостоятельной работе учащихся по заданиям теоретического и практического характера. По окончании этой части занятия учащимся предлагается домашнее задание по изучению теории и ее приложений. Вторая часть каждого занятия посвящена решению задач повышенной трудности и обсуждению решений особенно трудных или интересных задач. Эта форма проведения факультативных занятий может способствовать успешному переходу от форм и методов обучения в школе к формам и методам обучения в высших учебных заведениях.
Естественно также при проведении факультативных занятий в основном использовать методы изучения (а не обучения) математики, а также проблемную форму обучения.
При выборе методов и приемов обучения на факультативных занятиях необходимо учитывать содержание факультативного курса, уровень развития и подготовленности учащихся, их интерес к тем или иным разделам программы. Одно из главнейших требований к методам состоит в активизации мышления учащихся, развитие самостоятельности в различных формах ее проявления.
Как и в работе с математическими классами, на факультативах могут использоваться разнообразные формы и методы проведения занятий: лекции, практические работы, обсуждение заданий по дополнительной литературе, экскурсии и т.п. Рассмотрим некоторые из них.
Часть материала может быть изложена лекционно, особенно при синтезе и обобщении. Цель учителя показать – как проводить подобную организацию материала: некоторые детали доказательств можно опустить, из определений привести только самые главные, но конкретные методы решения задач изложить в таком виде, чтоб ясно прослеживался путь решения. Такие лекции полезно проводить по материалу, в котором уделяется большое внимание отработки навыков.
Иной тип лекций используется, когда целью служит не систематизация навыков, а общее развитие школьников, например, в отношении понимания прикладной роли математики. Здесь важно выделить не методы решения отдельных типов задач, а идеи, служащие основой для них, или же сами методы, но в обобщенной форме. В таких лекциях большое место занимает история, примеры из современной жизни и производства.
При проведении лекции возможны беседы с учениками, обсуждение возникающих по ходу рассказа вопросов, постановка задач и др.
Последняя форма работы – подготовка учениками рефератов, выполнение таких заданий важно, прежде всего, в отношении развития навыков самообразования, удовлетворение индивидуальных интересов учеников. Одновременно индивидуальное задание должно иметь ценность для всех участников факультативной группы. Следует стремиться к тому, чтобы подготовительные доклады заслушивались и обсуждались. К подготовке доклада можно привлечь несколько ребят, заранее изучивших его. Они могут выполнять роль ассистентов лектора или его оппонентов.
Очень большое значение для успешности усвоения материала подбор задач. Вводные задачи на факультативных занятиях преследуют цель включения учащихся в самостоятельную творческую работу; подчас учитель может намеренно привести задачу, способную поставить учеников в тупик.
Следует предусмотреть также в нужных местах изложения проблемные задачи, циклы для самостоятельного решения, задачи для закрепления и формирования навыков, исследовательские задачи.
Время выделенное программой для решения задач повышенной трудности, можно распределить в течении всего учебного года. Более сложные задачи можно рассмотреть на заключительных занятиях по темам. На этих же занятиях целесообразно ознакомить школьников с программами вступительных экзаменов и особенностям обучения в вузах.
Остановимся вкратце на использовании наглядных и технических средств обучения на факультативных занятиях. Оно во многих случаях позволяет активизировать познавательную деятельность, не говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения.
Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась в отдельных крупных городах благодаря энтузиазму математиков – ученых и учителей, студентов и аспирантов. Кажется, именно математики первыми заговорили о подготовке математической молодежи. А все другие предметные олимпиады возникли уже вслед за математическими.
К концу ХХ в. олимпиада превратилась в целое общественное движение со сложной иерархической организацией. Это движение берет начало в школах, проходит районный, городской, региональный этапы, общероссийский этап и завершается на международном уровне.
К середине 30-х годов многие советские ученые-математики пришли к мысли о необходимости сотрудничества со школой в деле подготовки математической смены. Будущего математика необходимо воспитывать с детства, и чем раньше – тем лучше. Никого не удивляет, что подготовка будущих балерины или музыканта начинается чаще всего в раннем детстве с 6-8 – летнего возраста. Объясняется это тем, что успешное овладение тонкостями балетного искусства или музыки в юношеском возрасте невозможно без специализированной подготовки в детстве, обеспечивающей развитие слуха и чувства ритма, гибкость суставов или подвижность пальцев и т.д. И каждый год, упущенный в детстве, впоследствии удается возместить лишь многими годами упорной работы.
Не следует думать, что в науке, и особенно в математике, дело обстоит как-либо иначе. Разумеется, подготовку будущего математика вовсе не обязательно (хотя вполне возможно) начинать с 6-8 – летнего возраста. Однако перекладывать эту работу целиком на Университет тоже нецелесообразно. Здесь, так же как в балетном искусстве или музыке, годы, упущенные в детстве, трудно компенсировать впоследствии. Дело в том, что работа в области математики требует известной гибкости ума, умение абстрактно мыслить, требует определенной логической культуры, отсутствие которых к моменту поступления в Университет невозможно компенсировать даже упорной работой в студенческие годы. Разумеется, все эти данные (в совокупности составляющие то, что обычно называют «математическими способностями») могут развиваться у подростка в период обучения в общеобразовательной школе без какой бы то ни было специализированной подготовки. Это – стихийный процесс появления математических самородков, конечно имевшие место во все времена и во всех странах. Например, известнейших индийский математик С. Рамануджан (1887-1920) воспитывался в атмосфере враждебности ко всему европейскому (и особенно английскому) и не получил в детстве, по существу, никакого математического образования.
Однако в 30-е годы стало ясно, что этот процесс стихийного формирования ученых не может удовлетворять все возрастающие потребности страны в квалифицированных математиках. Правда, всеобщее среднее образование позволяет надеяться на то, что одаренные, способные дети будут замечены школьным учителем, поддержка которого создаст стимулы для углубленной дополнительной работы. Однако эти надежды не всегда оправдываются. Ведь круглые «пятерки» по всем математическим предметам – весьма маловыразительный критерий, в котором отражается не только (а иногда и не столько!) математические способности, но и внимательность, аккуратность в работе, прилежание и даже хороший почерк. Напротив, скромные оценки по математическим предметам далеко не всегда свидетельствуют о математической не одаренности. Достаточно упомянуть о том, что видный советский математик, лауреат Ленинской премии, профессор М.М. Постников (да не обидится он на нас за разглашение этого секрета!) в школьные годы не входил в числе первых математиков школы; в его дневнике, бывало, проглядывали и «двойки» по математическим дисциплинам. Но даже в тех случаях, когда учитель правильно подмечает математическую «искру» в своем ученике, он не всегда может помочь ему в подборе дополнительных задач и дополнительной литературы, помочь раздуть эту искру в большой огонь, освещающий дорогу в будущее.
Между тем математические дарования, подобно музыкальным, проявляются обычно довольно рано. Более того, при правильном развитии ученого-математика наиболее крупные открытия зачастую делаются в весьма молодом возрасте. Так, например, убитый на дуэли в возрасте 20 лет французский математик Эварист Галуа (1811-1832) успел за свою короткую жизнь создать замечательную по глубине алгебраическую теорию, произведшую целый переворот в последующем развитии математики. Девятнадцатилетний К.Ф. Гаусс (1777-1855) успел опубликовать свои классические исследования о построениях циркулем и линейкой, а через несколько лет подарил миру книгу «Disquisitiones arithmeticae», равных которой можно немного указать в истории математической науки! Закон двойственности, прославивший замечательного советского математика, академика Л.С. Понтрягина, был найден им еще в студенческие годы.
Эти обстоятельства делают необходимым участие ученых-математиков в работе со школьниками. Инициаторами такой работы выступили в Ленинграде член-корреспондент АН СССР, профессор Б.Н. Делоне и профессор В.А. Тартаковский, а в Москве член-корреспондент АН СССР, профессор Л.Г. Шнирельман и профессор (ныне член-корреспондент АН СССР) Л.А. Люстерник. Весной 1934 г. в Ленинграде была проведена первая в Советском Союзе школьная математическая олимпиада. Одновременно по инициативе Л.А. Люстерника начала выходить серия математических книг, переназначенных специально для школьников («Популярная библиотека по математике»). С осени 1934 г. в Москве, в Институте математики АН СССР, начали регулярно читаться лекции по математике для учащихся старших классов. Но, не смотря на то, что к чтению лекций привлекались крупнейшие советские математики, посещались эти лекции довольно слабо – достаточно эффективные формы работы со школьниками не были еще найдены!
В этих условиях Правление Московского Математического Общества подхватило инициативу ленинградцев и приняло решение о проведении I Московской школьной математической олимпиады. К этому мероприятию математики отнеслись с большим воодушевлением. Достаточно сказать, что почти все профессора-математики МГУ вошли в оргкомитет олимпиады (А.Н. Колмогоров, Л.А. Люстерник, Л.Г. Шнирельман, В.Ф. Каган, С.Л. Соболев, С.А. Яновская и др.); председателем оргкомитета был президент Московского Математического Общества, член-корреспондент АН СССР (ныне академик) П.С. Александров.
В олимпиаде приняли участие 314 школьников, что считалось тогда большим успехом. Во втором, заключительном туре олимпиады приняли участие 120человек, из которых трое (Игорь Зверев, Коля Коробов и Аня Мышкис) получили первые премии и пятеро – вторые премии. В качестве премий победителям были вручены небольшие математические библиотечки. Кроме того, 44 школьника получили похвальные отзывы.
В 1934 году Ленинградским университетом по инициативе группы преподавателей (профессора Б. Н. Делоне, профессора Г. М. Фихтенгольц и др.) была проведена первая в нашей стране математическая олимпиада школьников. Этот почин был подхвачен математическими коллективами многих других городов. Уже в следующем (1935 г) году математическая олимпиада была проведена в Москве. Математические олимпиады и в отдельных классах. В последнее время проводятся областные, краевые, республиканские и всесоюзные математические олимпиады.
Говоря об олимпиаде, следует отметить, что до сих пор эта форма внеклассной работы с учащимися является своеобразным итогом проделанной работы (чаще всего кружковой). Олимпиада – соревнование, которое, несомненно, стимулирует рост учащихся в смысле математического образования, воспитывает у них математическое мышление, интерес к математике, настойчивость – желание не отступать от тех, которые успешно справляются с олимпиадным заданием; часто именно участие в олимпиаде и подготовка к ней побуждает учащихся к самостоятельной работе, вырабатывает умение работать с научно-популярной литературой и т.д.
Математические олимпиады проводятся на различных уровнях: школьные, районные, городские, областные, республиканские, общесоюзные и международные. В проведении областных и республиканских олимпиад активно участвуют педагогические институты и университеты; общесоюзная олимпиада проводится под эгидой Московского государственного университета им. М. В. Ломоносова.
Олимпиады также оказывают положительное влияние и на общий уровень преподавания математики, во многом позволяют выявить качество математических знаний учащихся и, кроме того, в какой-то степени ориентируют учителя, характеризуя уровень той математической подготовки, которая считается высокой. Однако следует обратить внимание на то не мало важное обстоятельство, что олимпиады не являются серьезным источником новой, интересующих учащихся информации и потому не могут считаться основной формой углубленной математической подготовки молодежи.
Для руководства всей подготовительной работой внутришкольных олимпиад нужно уже в начале учебного года выделить оргкомитет. В состав его входят обычно два-три учителя математики и несколько учеников – представителей математических кружков.
Оргкомитет проявляет инициативу в организации математического вечера, лекций и других внеклассных мероприятий внутри школы, отбирает задачи для олимпиады и для подготовки к ней, отбирает победителей олимпиады и т.д.
Отбор задач для олимпиады необходимо начать заблаговременно, задолго до олимпиады, проводить его с учетом того, какие задачи предложены учащимся для подготовке к олимпиаде. Всей этой работой ведает специально выделенный член оргкомитета (учитель). К отбору задач к олимпиаде привлекаются также другие учителя математики.
Задачи, предлагаемые на олимпиаде, не требуют знаний, выходящих за рамки школьной программы. Обычно это задачи, требующие для своего решения проявление смекалки, самостоятельной мысли, хорошего пространственного воображения, известных навыков к логическому мышлению, а также твердого и неформального знания основных понятий и методов школьного курса математики. Задачи с громоздкими решениями, чисто тренировочные, требующие лишь формального применения теорем и формул, обычно не включаются в олимпиадные задания.
Математические экскурсии – исключительно интересная, но сравнительно редко применяемая форма внеурочных занятий. Не следует думать, что они сводятся только к геодезическим работам на местности. Во время экскурсии ученик видит, где на практике встречаются и применяются различные геометрические фигуры, изученные им в школе, знакомится с применениями математики в различных областях народного хозяйства. На экскурсии ученик видит немало случаев, когда приходится использовать известные ему формулы для вычисления тех или иных геометрических величин (длин, площадей, объемов). Хорошо поставленные экскурсии укрепят уверенность учащегося в том, что с математикой действительно сталкиваешься на каждом шагу, что «математика всюду», что она действительно необходима человечеству. У учащихся значительно повышается интерес к этому предмету. Хорошо подготовленные экскурсии приводят к лучшему пониманию учащимися отдельных вопросов курса математики.
Полезной формой внеклассной работы является также стенная математическая печать. Важно, чтобы она была действительной, т.е. содержащиеся в ней материалы использовались активно. Хорошо, когда часть материалов в газете представляет учебный интерес для всего класса; другая часть основывается на недавно пройденном в классе материале, углубляя его в определенном отношении, и, наконец, имеются занимательные задачи и задачи повышенной трудности, по которым систематически проводятся конкурсы решений.
Важное место во внеклассной работе по математике может занять изготовление учащимися различных моделей и наглядных пособий. Этот вид работы имеет большое воспитательное значение, кроме того, в процессе изготовления этих пособий учащиеся могут связать изучение математики с выработкой трудовых навыков. Желательно, чтобы подготовительные модели и пособия использовались в учебном процессе.
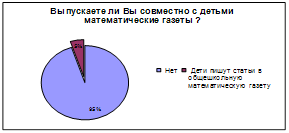
Для выпуска математической стенгазеты не обязательно наличие математического кружка. Иногда математическая стенгазета выпускается в период организации кружка, когда нужно привлечь внимание учащихся по кружку. Специальный номер математической стенгазеты выпускается к школьному математическому вечеру.
Однако мы будем ориентироваться на тот наиболее важный и наиболее реальный случай, когда газета выходит как орган кружка. Основная цель такой газеты – пропаганда математических знаний среди учащихся, не состоящих в кружке, повышение их интереса к математике, привлечение их к кружку, освещение опыта работы кружка. Известную часть газеты занимают материалы, которые не рассматриваются на заседаниях кружка. Газета как бы дополняет кружковые занятия.
Школьникам, выпускающим газету, эта работа приносит большую пользу, так как приходится подбирать материалы для газеты, а для этого они знакомятся с различными книгами, выбирают из них нужный материал, отделяют самое главное, литературно обрабатывают отобранное. Все это благотворно сказывается на расширении математического кругозора учащихся, на их речи и грамотности.
Содержание стенгазеты должно быть разнообразным, в противном случае она очень скоро надоест учащимся.
Каждый номер стенной газеты должен состоять из передовой статьи, посвященной какой-нибудь определенной теме или событию, ряда небольших заметок и конкурсных задач.
Если номер приурочен к юбилейной дате ученого-математика, то предложенные задачи и заметки должны быть по возможности связаны с именем этого ученого.
В коротких заметках обычно сообщают о новом в науке и технике, о результатах конкурсов и олимпиад. Полезно помещать решение отдельных задач с обязательным указанием фамилий учеников, решивших эти задачи. Конкурсные задачи должны быть разной степени трудности. Легкие задачи нужны для того, чтобы заинтересовать более равнодушных и заставить поверить в свои силы более слабых.
С интересом читают учащиеся коротенькие сообщения под рубрикой «А знаете ли вы?» Материал для этих заметок, а также сообщения о новостях науки и техники можно подбирать из различных журналов, газет, из книг по занимательной математике, физике, астрономии и механике.
С повышенным интересом относятся учащиеся к различного рода софизмам. Парадоксальный вывод привлекает учащихся и заставляет невольно искать ошибку.
Математическая газета должна выпускаться регулярно и не реже одного раза в месяц.
В математической фотогазете помещаются фотографии выдающихся математиков, фотографии людей, старинных книг по математике, фотографии победителей математических соревнований и т.д. Каждая фотография снабжается кратким объяснительным текстом.
Фотомонтажи обычно бывают на определенную тему. На большом листе бумаги, располагают фотографии, и под каждой помещается, краткая биография ученого.
Относительно содержания альбомов можно повторить все то, что было сказано относительно монтажей. Заслуживает внимание изготовление альбома.
Интересные высказывания о математике могут быть использованы в математических беседах учителями, на занятиях математических кружков, при проведении других видов внеурочных занятий. В школе можно повесить отдельные плакаты с высказываниями выдающихся людей о математической науке.
Любителям математики может быть предложено в течении сравнительно большого промежутка времени (недели, месяца) выполнить определенное задание. Учащийся имеет право выполнить это задание где и когда хочет, лишь бы в срок. Такой вид состязания называется математическим конкурсом. Победителем конкурса объявляется тот, кто лучше других справится с этим заданием. Часто темой конкурса является решение всякого рода задач. Они предлагаются иногда учителем и вывешиваются в классе. Все задание желательно разбить на несколько частей (серий), по 3-5 задач в каждой серии. Полное решение каждой задачи оценивается в определенное число очков. Отбор победителей лучше производить по числу набранных очков. Темой конкурса могут быть некоторые вопросы истории математики, изготовление моделей и составление задач. Конкурсы могут сыграть немалую роль в привитии учащимся вкуса к математическому чтению. Полезны конкурсы на лучшее математическое сочинение учащихся.
Математические викторины это одна из наиболее легко организуемых форм математических соревнований. Математическую викторину можно провести на математическом вечере, на общешкольных и классных вечерах, посвященных математике, на некоторых заседаниях математического кружка.
В викторине может принять участие каждый желающий. Предлагают обычно 6-12 вопросов и задач. Викторина проводится по-разному, в зависимости от числа участников.
Первая форма. Каждый вопрос или задача зачитывается учителем или школьником, проводящим викторину. На обдумывание ответа дается несколько минут. Отвечает тот, кто первым поднимет руку. Если ответ не полный, то можно предоставить возможность высказаться еще и другому ученику викторины. За полный ответ присуждается два очка, за неполный, но удовлетворительный - одно очко. Побеждают те ученики, которые набрали больше всего очков. Некоторые задачи и вопросы только зачитываются, условия других задач могут быть записаны на доске.
Вторая форма. Тексты всех вопросов и задач записываются (предварительно) на доске, или на отдельных плакатах, или раздаются школьникам, написанных на отдельных листах. Каждому участнику выдается лист бумаги, на котором они записывают ответ и краткое объяснение к каждому вопросу и задаче, а также свою фамилию, имя, класс. Этот листок он сдает в жюри викторины. Через определенный срок после начала викторины (минут через 30) прием листков от участников викторины прекращается, жюри проверяет решения и выявляет победителей викторины.
Задачи для викторины должны быть с легко обозримым содержанием, не громоздкие, не требующие сколько-нибудь значительных выкладок или записей, в большинстве своем доступные для решения в уме. Помимо задач, в викторину можно включить также различного рода вопросы по математике и по истории математики.
Среди различных источников новых знаний по математике одно из первых мест занимает книга. Всю литературу, знакомящую школьников с основами математики и с их применением, можно разделить на учебную (стабильные учебники, дидактические материалы, сборники задач, справочники) и дополнительную (научно-популярные книги и статьи, сборники задач олимпийского характера).
В процессе обучения математике учащиеся весьма широко используют основную учебную литературу; однако дополнительную литературу по математике все еще читают весьма немногие, причем это чтение не носит организационного характера.
Между тем обучающее значение работы учащихся с дополнительной литературой по математике весьма велико, так как именно эта работа способствует не только повышению качества знаний учащихся, но и развитию у них устойчивого интереса к математике.
Немалое обучающее и развивающее значение имеют также умения и навыки работы с математической литературой.
Опыт, приобретаемый школьниками в процессе работы с учебной литературой, оказывается недостаточным для успешной работы с дополнительной литературой. Поэтому умения и навыки работы школьников с математической литературой необходимо целенаправленно развивать, причем развивать систематически.
Эффективность самостоятельной работы учащихся с учебной и дополнительной литературой вообще (и математической в частности) зависит и от некоторых факторов (установка, вдохновение, интерес, волевое усилие, самостоятельность, трудолюбие и т.п.).
Одним из важнейших условий успешной работы с книгой является наличие особого состояния умственной деятельности, называемого установкой.
Под установкой, понимают готовность к действию в определенном направлении, т.е. своеобразное состояние психики, возникающее при единстве мотива деятельности (потребности в ней) и ситуации, которая ему соответствует.
Применительно к работе с книгой такая установка способствует активизации внимания и памяти, способствует точности восприятия содержания, помогает выделять в тексте главную мысль, развивает способность творчески воспринимать получаемую информацию и т.д., т.е. способствует выработке умений и навыков самостоятельного приобретения новых знаний в процессе работы над литературой.
Поэтому целенаправленность работы учащихся с дополнительной (и учебной) литературой, наличие сильной мотивации (соответствия познавательных интересов и деятельности) во многом определяют эффективность этого важного вида учебной деятельности.
Проведение школьных предметных недель стало теперь традицией во многих учебных заведениях. В большинстве случаев они проводятся один раз в год. Неделя математики в нашей школе проходит в конце января. В подготовке участвуют все учителя математики. Им помогают старшеклассники. Примерно за две-три недели в каждом классе создаются инициативные группы из учеников, проявляющих повышенный интерес к математике. Руководят работой групп учителя, работающие в этих классах. Задача каждой группы – подготовить и провести внеклассные мероприятия с одноклассниками, выпустить стенгазету, выступить с лекцией или докладом по математике, помочь учителю в проведении олимпиады или конкурса. В первый день недели на общем стенде вывешиваются стенные газеты. Они могут быть посвящены какой-нибудь определенной теме или математическому событию, состоять из ряда небольших заметок или конкурсных задач. Материал для газет подбирается из различных журналов, книг по занимательной математике, астрономии, механике, физике. Все это благотворно сказывается на развитии кругозора учащихся, на их навыках чтения литературы по математике, на их речи, грамотности. Уже само название газеты должно привлечь внимание учащихся. В конце недели авторы лучших газет награждаются призами.
В течении следующих дней в классах проводятся математические КВН, конкурсы, викторины, вечера. Материал для подготовки к этим мероприятиям подбирается из газет «Математика» – приложение к газете «Первое сентября», журналов «Математика в школе» и другой литературы.
В завершение недели проводится школьная математическая олимпиада.
Руководит проведением олимпиады школьный оргкомитет под председательством директора или завуча. На олимпиаду допускаются все желающие участвовать в ней дети. Первые задания – более легкие – выполняют почти все успевающие ученики. Нужно дать почувствовать каждому ребенку, даже слабому, что учителя верят в их силы и возможности.
Пусть даже незначительный успех на олимпиаде вселит в них уверенность в своих силах, а это может привести и к более усиленным занятиям, и к действительным успехам. Победители олимпиады награждаются призами и направляются на районные олимпиады.
Неделя заканчивается общешкольным математическим вечером, на котором подводятся итоги, отмечаются лучшие работы.
Похожие работы
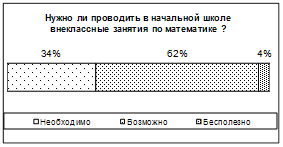
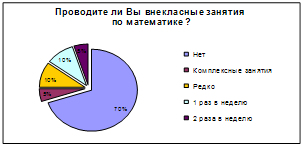
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...
... , внутрипредметные и комплексные семинары, интегрированные уроки, практикумы, экскурсии, внеклассная работа в школе). В данной курсовой работе предусматривается изучение процесса формирования познавательных умений учащихся во внеклассной работе. Глава 2. Содержание внеклассной работы Урок даже самый удачный имеет один недостаток: он спрессован во времени и не допускает отвлечений, даже когда ...
... или факультатива. Для учителя полученные данные нужны для эффективного применения индивидуального подхода к школьникам во внеурочной работе, корректировки своей работы, направленной на развитие интереса учащихся в ходе внеурочных занятий. В противном случае первоначальный интерес к математике, не получая подкрепления и развития, гаснет и ученик прекращает посещать внеурочные мероприятия. Более ...
... при ошибке в его выборе, учитывать по уровневый подход. 4. Математика должна входить в набор обязательных учебных предметов любого из профилей.2 МАТЕМАТИЧЕСКИЙ ФАКУЛЬТАТИВ КАК ВЕДУЩАЯ ФОРМА ПРОФИЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ В ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЕ2.1. Организационно-педагогические условия успешного функционирования математических факультативов Еще на рубеже XIX и XX вв. некоторые ...
0 комментариев