Навигация
Развитие младших школьников в процессе обучения математике
РАЗВИТИЕ МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИКЕ
Что такое развивающее обучение?
Термин «развивающее обучение» активно используется в психологической, педагогической и методической литературе. Тем не менее, содержание этого понятия остается до сих пор весьма проблематичным, а ответы на вопрос: «Какое обучение можно назвать развивающим?» довольно противоречивы. Это, с одной стороны, обусловлено многоаспектностью понятия «развивающее обучение», а с другой стороны, некоторой противоречивостью самого термина, т.к. вряд ли можно говорить о «неразвивающем обучении». Бесспорно, любое обучение развивает ребенка.
Однако нельзя не согласиться с тем, что в одном случае обучение как бы надстраивается над развитием, как говорил Л.С. Выготский, «плетется в хвосте» у развития, оказывая на него стихийное влияние, в другом – целенаправленно обеспечивает его (ведет за собой развитие) и активно использует для усвоения знаний, умений, навыков. В первом случае мы имеем приоритет информационной функции обучения, во втором – приоритет развивающей функции, что кардинально меняет построение процесса обучения.
Как пишет Д.Б. Эльконин – ответ на вопрос, в каком соотношении находятся эти два процесса, «осложнен тем, что сами категории обучения и развития разные.
Эффективность обучения, как правило, измеряется количеством и качеством приобретенных знаний, а эффективность развития измеряется уровнем, которого достигают способности учащихся, т. е. тем, насколько развиты у учащихся основные формы их психической деятельности, позволяющей быстро, глубоко и правильно ориентироваться в явлениях окружающей действительности.
Давно замечено, что можно много знать, но при этом не проявлять никаких творческих способностей, т. е. не уметь самостоятельно разобраться в новом явлении, даже из относительно хорошо известной сферы науки»[1].
Не случайно термин «развивающее обучение» методисты используют с большой осторожностью. Сложные динамические связи между процессами обучения и психического развития ребенка не являются предметом исследования методической науки, в которой реальные, практические результаты обучения принято описывать на языке знаний, умений и навыков.
Так как изучением психического развития ребенка занимается психология, то при построении развивающего обучения методика несомненно должна опираться на результаты исследований этой науки. Как пишет В.В.Давыдов, «психическое развитие человека – это, прежде всего, становление его деятельности, сознания и, конечно, всех «обслуживающих» их психических процессов (познавательных процессов, эмоций и т. д.)»[2]. Отсюда следует, что развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения.
Из курса дидактики вам известно, что эта деятельность может быть репродуктивной и продуктивной. Они тесно связаны между собой, но в зависимости от того, какой вид деятельности преобладает, обучение оказывает различное влияние на развитие детей.
Репродуктивная деятельность характеризуется тем, что ученик получает готовую информацию, воспринимает ее, понимает, запоминает, затем воспроизводит. Основная цель такой деятельности – формирование у школьника знаний, умений и навыков, развитие внимания и памяти.
Продуктивная деятельность связана с активной работой мышления и находит свое выражение в таких мыслительных операциях, как анализ и синтез, сравнение, классификация, аналогия, обобщение. Эти мыслительные операции в психолого–педагогической литературе принято называть логическими приемами мышления или приемами умственных действий.
Включение этих операций в процесс усвоения математического содержания – одно из важных условий построения развивающего обучения, так как продуктивная (творческая) деятельность оказывает положительное влияние на развитие всех психических функций. «... организация развивающего обучения предполагает создание условий для овладения школьниками приемами умственной деятельности. Овладение ими не только обеспечивает новый уровень усвоения, но дает существенные сдвиги в умственном развитии ребенка. Овладев этими приемами, ученики становятся более самостоятельными в решении учебных задач, могут рационально строить свою деятельность по усвоению знаний»[3].
Рассмотрим возможности активного включения в процесс обучения математике различных приемов умственных действий.
3.2. Анализ и синтез
Важнейшими мыслительными операциями являются анализ и синтез.
Анализ связан с выделением элементов данного объекта, его признаков или свойств. Синтез – это соединение различных элементов, сторон объекта в единое целое.
В мыслительной деятельности человека анализ и синтез дополняют друг друга, так как анализ осуществляется через синтез, синтез – через анализ.
Способность к аналитико–синтетической деятельности находит свое выражение не только в умении выделять элементы того или иного объекта, его различные признаки или соединять элементы в единое целое, но и в умении включать их в новые связи, увидеть их новые функции.
Формированию этих умений может способствовать: а) рассмотрение данного объекта с точки зрения различных понятий; б) постановка различных заданий к данному математическому объекту.
Для рассмотрения данного объекта с точки зрения различных понятий младшим школьникам при обучении математике обычно предлагаются такие задания:
Прочитай по–разному выражения 16 – 5 (16 уменьшили на 5; разность чисел 16 и 5; из 16 вычесть 5).
Прочитай по–разному равенство 15–5=10(15 уменьшить на 5, получим 10; 15 больше 10 на 5; разность чисел 15 и 5 равна 10;
15 – уменьшаемое, 5 – вычитаемое, 10 – разность; если к разности (10) прибавить вычитаемое (5), то получим уменьшаемое (15); число 5 меньше 15 на 10).
Как по–разному можно назвать квадрат? (Прямоугольник, четырехугольник, многоугольник.)
Расскажи все, что ты знаешь о числе 325. (Это трехзначное число; оно записано цифрами 3, 2, 5; в нем 325 единиц, 32 десятка, 3 сотни; его можно записать в виде суммы разрядных слагаемых так: 300+20+5; оно на 1 единицу больше числа 324 и на 1 единицу меньше числа 326; его можно представить в виде суммы двух слагаемых, трех, четырех и т.д.)
Конечно, не следует стремиться к тому, чтобы каждый ученик произносил этот монолог, но, ориентируясь на него, можно предлагать детям вопросы и задания, при выполнении которых они будут рассматривать данный объект с различных точек зрения.
Чаще всего это задания на классификацию или на выявление различных закономерностей (правил).
Например:
1. По каким признакам можно разложить пуговицы в две коробки?
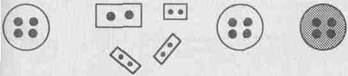
Рассматривая пуговицы с точки зрения их размеров, мы положим в одну коробку 4 пуговицы, а в другую 3,
– с точки зрения цвета: 1 и 6,
– с точки зрения формы: 4 и 3.
2. Разгадай правило, по которому составлена таблица, и заполни пропущенные клетки:
| 4 | 6 | 9 | 3 | 8 | 6 | 5 | 2 | ||
| 5 | 7 | 8 | 2 | 4 | 6 |
Увидев, что в данной таблице две строки, учащиеся пытаются выявить определенное правило в каждой из них, выясняют, на сколько одно число меньше (больше) другого. Для этого они выполняют сложение и вычитание. Не обнаружив закономерность ни в верхней, ни в нижней строке, они пытаются анализировать данную таблицу с другой точки зрения, сравнивая каждое число верхней строки с соответствующим (стоящим под ним) числом нижней , строки. Получают: 4<5 на 1; 6<7 на 1; 9>8 на 1; 3>2 на 1. Если под числом 8 записать число 9, а под числом 6 – число 7, то имеем:
8<9 на 1; 6<7 на 1, значит, 5>П на 1, П>4 на 1.
Аналогично можно сравнивать каждое число нижней строки с соответствующим (стоящим над ним) числом верхней строки.
Возможны такие задания с геометрическим материалом.
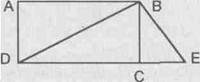
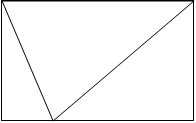
• Найди отрезок ВС. Что ты можешь рассказать о нем? (ВС – сторона треугольника ВСЕ; ВС – сторона треугольника DBC; ВС меньше, чем DC; ВС меньше, чем АВ; ВС – сторона угла BCD и угла ВСЕ).
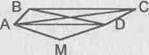
• Сколько отрезков на данном чертеже? Сколько треугольников? Сколько многоугольников?
Рассмотрение математических объектов с точки зрения различных понятий является способом составления вариативных заданий. Возьмем, например, такое задание: «Запишем все четные числа от 2 до 20 и все нечетные числа от 1 до 19». Результат его выполнения – запись двух рядов чисел:
2, 4, 6, 8, 10,12,14,16,18,20 1,3,5,7,9, 11, 13, 15, 17, 19
Используем теперь эти математические объекты для составления заданий:
• Разбей числа каждого ряда на две группы так, чтобы в каждой были числа, похожие между собой.
• По какому правилу записан первый ряд? Продолжи его.
• Какие числа нужно вычеркнуть в первом ряду, чтобы каждое следующее было на 4 больше предыдущего?
• Можно ли выполнить это задание для второго ряда?
• Подбери из первого ряда пары чисел, разность которых равна 10
(2 и 12, 4 и 14, 6 и 16, 8 и 18, 10 и 20).
• Подбери из второго ряда пары чисел, разность которых равна 10 (1 и 11,3 и 13, 5 и 15, 7 и 17, 9 и 19).
• Какая пара «лишняя»? (10 и 20, в ней два двузначных числа, во всех других парах двузначное число и однозначное).
• Найди в первом ряду сумму первого и последнего числа, сумму вторых чисел от начала и от конца ряда, сумму третьих чисел от начала и от конца ряда. Чем похожи эти суммы?
• Выполни это же задание для второго ряда. Чем похожи полученные суммы?
• Задание 80. Придумайте задания, в процессе выполнения которых учащиеся будут рассматривать данные в них объекты с различных точек зрения.
Похожие работы
... , если оно вводится целенаправленно, осознанно, с учетом характера материала, сравниваемых объектов, возраста и уровня развития школьников. РАЗДЕЛ 2. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПО ФОРМИРОВАНИЮ УМСТВЕННОГО ПРИЕМА СРАВНЕНИЯ У МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ИЗУЧЕНИЯ МАТЕМАТИКИ 2.1. Методика по развитию и формированию сравнения у младших школьников в процессе изучения математики ...
... проблемного характера, задания, связанные с классификацией, анализом и синтезом, опорные схемы. Всё это составляет приёмы познавательной деятельности учащихся. Глава 3. Приёмы активизации учащихся в процессе обучения математике в начальных классах при изучении нумерации многозначных чисел 3.1. Сущность приёмов активизации Для того, чтобы добиться активности учащихся на уроке математике, ...
... школ с. Большая Малышка и Соколовской Кызылжарского района Северо-Казахстанской области в количестве 30 человек. Изучение роли межпредметных связей уроков русского языка с другими учебными предметами в начальной школе в развитии письменной речи младшего школьника потребовало экспериментального обоснования и проверки эффективности данного предположения. Опытно-экспериментальная работа включала ...
... и даже превратился в черту характера. ГЛАВА 2. ИЗУЧЕНИЕ ОПЫТА РАБОТЫ УЧИТЕЛЕЙ НАЧАЛЬНЫХ КЛАССОВ ПО ФОРМИРОВАНИЮ САМОКОНТРОЛЯ У МЛАДШИХ ШКОЛЬНИКОВ 2.1 Особенности формирования самоконтроля у младших школьников Е.С. Рубинский в качестве путей обучения школьников самоконтролю предлагает «наглядный контроль со стороны учителя, взаимоконтроль учащихся и на этой основе - самоконтроль ...

0 комментариев