Выполните умножение двух выражений и проанализируйте полученные результаты для каждого примера

1.   Выполните умножение двух выражений и проанализируйте полученные результаты для каждого примера.

Вариант А.

а) (3х+4у)(3х–4у); б) (0,5а+3b)(0,5а–3b); в) .

Вариант В.

а) (5х+2у)(5х–2у); б) (2а+0,3с)(2а–0,3с); в) .

Вариант С.

а) (2х+3у)(2х–3у); б) (5х+4у)(5х–4у); в) (9+7с)(9–7с).

Вариант D.

а) (х+7)(х–7); б) (2а+5b)(2a–5b); в) (4х+6у)(4х–6у).

Образец: .

Выполните аналогично остальные примеры, заполните таблицу.

Что дано?	Что получилось?	Как получилось?
Произведение суммы и разности двух одночленов (х+7)(х–7) (2а+5b)(2a–5b) (4х+6у)(4х–6у)	Разность квадратов х2–49

2.   Используя результаты задания 1, не выполняя умножения, напишите сразу ответ.

Вариант А.

а) (а+b)(а–b); б) (7х+8у)(7х–8у); в) (0,3а+0,4b²) (0,3а–0,4b²).

Вариант В.

а) (а+b)(а–b); б) (4х+5у)(4х–5у); в) (2а²+0,5b) (2а²–0,5b).

Вариант С.

а) (а+b)(а–b); б) (8х+5у)(8х–5у); в) (6у+7) (6у–7).

Вариант D.

а) (а+b)(а–b); б) (х+у)(х–у); в) (3а+4b) (3а–4b).

3.   Подставьте вместо * пропущенные данные так, чтобы получилось верное тождество.

Вариант А.

а) ; б) .

Вариант В.

а) (7с+2р)(7с–2р)=*; б) .

Вариант С.

а) (х+5)(х–5)=*; б) .

Вариант D.

а) б) (2b+3)(2b-3)=*.

4.   Подведите итоги своей работы.

Варианты А, В.

а) Запишите полученное тождество; б) сформулируйте (устно) правило.

Вариант С.

а) Запишите полученное тождество: (а+b)(а–b)=…

б) Чему равно произведение суммы и разности двух одночленов?

в) Как найти произведение суммы и разности двух одночленов?

Вариант D.

а) Запишите полученное тождество: (а+b)(а–b)=…

б) Прочтите правило в учебнике.

в) Как найти произведение суммы и разности двух одночленов?

Приложение 3.

Группа А

1.   Упростите выражение:

a)   2с(1+с)–(с–2)(с+4);

b)   (у+2)²–2у(у+2);

c)   30х+3(х–5)²;

d)   (b²+2b)²–b²(b–1)(b+1)+2b(3–2b²).

2.   Разложите на множители:

a)   4а–а³;

b)   ах²+2ах+а;

c)   ;

d)   а+а²–b–b².

3.   Докажите, что выражение с²–2с+12 может принимать лишь положительные значения.

Группа Б.

1.   Докажите, что при любом целом п значение выражения (2п–3)²–(4п–1)(п+6) кратно 5.

2.   Какое значение принимает выражение а(а+2)+с(с–2)–2ас при а–с=7?

3.   Найдите наименьшее значение выражения 4х²–4х+11.

4.   Докажите, что если к произведению трех последовательных целых чисел прибавить среднее их них, то получится куб среднего числа.

5.   Разложите на множители:

a)   а²+4ab–3a²b–6ab²+4b²;

b)   (a+b+c)²–(a–b–c)².

Приложение 4.

Задачи 1 уровня.

1.   Точка М не лежит в плоскости прямоугольника ABCD. Докажите, что CD параллельна плоскости АВМ.

2.   Докажите, что через любую из двух скрещивающихся прямых можно провести плоскость, параллельную другой прямой.

3.   Сторона АС треугольника АВС параллельна плоскости α, а стороны АВ и ВС пересекаются с этой плоскостью в точках М и Р. Докажите, что треугольники АВС и МВР подобны.

Задачи 2 уровня.

1.  

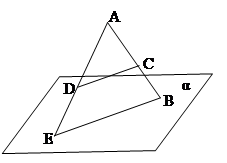Точка В лежит в плоскости α, отрезок CD параллелен этой плоскости, CD=12 см, АВ:СВ=4:3. Докажите, что прямая AD пересекает плоскость α в некоторой точке Е, и найдите отрезок ВЕ.

2.   Даны две скрещивающиеся прямые. Как провести через них две параллельные плоскости?

3.   Через данную точку пространства проведите прямую, пересекающую каждую из двух скрещивающихся прямых.

Творческие задачи.

1.   В правильной треугольной пирамиде SABC через вершину С и середину ребра SA проведите сеение пирамиды, параллельное SB. На ребре АВ взята точка F так, что AF:FB=3:1. Через точку F и середину ребра SC проведена прямая. Будет ли эта прямая параллельна плоскости сечения?

Список литературы.

1.   Алгебра: Учебник для 7 классов средней школы / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.; Под редакцией Теляковского С.А. – М.: Просвещение, 1993.

2.   Антропова М.В., Манке Г.Г., Кузнецова Л.М., Бородкина Г.В. Индивидуально-дифференцированное обучение в гимназии // Педагогика. 1996. №5.

3.   Арутюнян Е.Б., Глазков Е.Б., Левитас Г.Г. Взаимообучение школьников на уроках математики // Математика в школе. 1988. №4. – С.49.

4.   Атанасян Л.С., Бутузов В.Ф., С.Б. Кадомцев и др. Геометрия: Учебник для 10-11 классов средней школы. – М.: Просвещение, 1994.

5.   Белошистая А.В. Обучение математике с учетом индивидуальных особенностей ребенка // Вопросы психологии. 2001. №5.

6.   Болтянский В.Г., Глейзер Г.Д. К проблеме дифференциации школьного математического образования // Математика в школе. 1988. №3. – С.9.

7.   Веселаго И.А., Левина М.З. Структура коллектива и обучение // Математика в школе. 1994. №4. – С. 47.

8.   Воробьева Л.А. Дифференцированный контроль знаний по теме “Параллелограмм” // Математика в школе. 1993. №2. – С.14.

9.   Гильбух Ю.З. Идеи дифференцированного обучения в отечественной педагогике // Педагогика. 1994. №5.

10.        Грузин А.И., Кузнецова А.Ф., Михеева Е.Я. Одна из форм коллективной деятельности учащихся // Математика в школе. 1989. №5. – С.30.

11.        Дахин А.Н. К вопросу о разноуровневом обучении // Математика в школе. 1993. №4. – С.39.

12.       Дорофеев Г.В., Кузнецова Л.В., Суворова С.Б., Фирсов В.В. Дифференциация в обучении математике // Математика в школе. 1990. №4. – С.15.

13.       Жильцов П.А., Асирян М.А. Учебно-воспитательный комплекс с дифференцированным обучением // Педагогика. 1997. №4.

14.        Капиносов А.Н. Уровневая дифференциация при обучении математике в V-IX классах // Математика в школе. 1990. №5. – С.16.

15.        Котов В.В. Организация на уроках коллективной деятельности учащихся. – Рязань, 1977.

16.        Лийметс Х.Й. Групповая работа на уроке. – М.: “Знание”, 1975.

17.        Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов пед. ин-тов / А.Я. Блох, Е.С. Канин, Н.Г. Килина и др.; Сост. Р.С. Черкасов, А.А. Столяр. – М.: Просвещение, 1985.

18.        Морозова Л.В. Из опыта дифференцированного обучения // Математика в школе. 1998. №6. – С.37.

19.        Общая психология. Учебник для студентов педагогических институтов. Под редакцией профессора А.В. Петровского. Издание 2-е, дополненное и переработанное М., “Просвещение”, 1976.

20.        Осмоловская И. Нужны вариативность, гибкость и готовность удовлетворить потребности каждого ученика // Директор школы. 1994. №5. – С.28.

21.       Осмоловская И. Практика дифференцированного обучения: попытка систематизации // Школа. 1996. №6. – С.45.

22.        Осмоловская И. Процесс, адаптированный к особенностям школьника // Директор школы. 2001. №10. – С.62.

23.        Осмоловская И.М. Организация дифференцированного обучения в современной общеобразовательной школе. – М.: Издательство “Институт практической психологии”; Воронеж: Издательство НПО “МОДЭК”, 1998.

24.        Педагогика. Учебное пособие для студентов педагогических вузов и педагогических колледжей./Под ред. П.И. Пидкасистого. – М.: Педагогическое общество России, 1998.

25.        Погорелов А.В. Геометрия. Учебное пособие для 6-10 классов средней школы. – М.: Просвещение, 1982.

26.        Попков В.А. Дифференцированное обучение и формирование профессиональной элиты // Педагогика. 1998. №1.

27.        Рыбников К.А. К вопросу о дифференциации обучения // Математика в школе. 1988. №5. – С.16.

28.        Саранцев Г.И. Общая методика преподавания математики: учебное пособие для студентов математических специальностей педагогических вузов и университетов. – Саранск: Тип. “Красный Октябрь”, 1999.

29.        Саранцев Г.И., Корольков И.Г. Примеры многовариативных самостоятельных работ // Математика в школе. 1994. №4. – С.20.

30.        Селевко Г.К. Современные образовательные технологии: учебное пособие. – М.: Народное образование, 1998.

31.        Симакова Т.И. Применение типовых расчетов при дифференцированном обучении // Математика в школе. 1995. №4. – С.17.

32.        Уваров А.Ю. Кооперация в обучении: групповая работа: Учебно-методическое пособие. – М.: МИРОС, 2001.

33.        Унт И. Индивидуализация и дифференциация обучения. – М.: Педагогика, 1990.

34.       Урок в восьмилетней школе/под ред. М.А. Данилова. – М.: Просвещение, 1966.

35.        Утеева Р.А. Групповая работа как одна из форм деятельности учащихся на уроке // Математика в школе. 1985. №2.

36.        Утеева Р.А. Дифференцированные формы учебной деятельности учащихся // Математика в школе. 1995. №5. – С.32.

37.        Утеева Р.А. Формы учебной деятельности учащихся на уроке // Математика в школе. 1995. №2. – С.33.

38.        Чередов И.М. Формы учебной работы в средней школе: Кн. для учителя. – М.: Просвещение, 1988.

39.        Юркина С.Н. О дифференцированном обучении математике // Математика в школе. 1990. №3. – С.13.