Сутність та роль усних обчислень у початковому курсі математики
Види вправ для усних обчислень
Розв’язування рівнянь. Як усні вправи пропонують рівняння. Це насамперед найпростіші рівняння (х+2=10) і складніші (15·х- - 9 = 51)
Шляхи вдосконалення навичок усних обчислень у молодших школярів
Гра "Мовчанка" (рис. 2)
Зовнішні умови, що визначаються суспільними засобами життє-діяльності людини. Ці джерела активності називають спонуканнями [53, 42]
Методика експериментального дослідження
Дидактичні ігри
Аналіз результатів експериментального дослідження
Навигация
Види вправ для усних обчислень
Усні обчислення на уроках математики в початкових класах
111696
знаков
4
таблицы
10
изображений
1.2 Види вправ для усних обчислень
Вправи з усних обчислень мають пронизувати увесь урок. Їх можна поєднувати з перевіркою домашніх завдань, закріпленням вивченого матеріалу, опитуванням учнів. Поряд з цим у практиці роботи вчителів є хороша традиція: на кожному уроці спеціально відводити 5-7 хв для усних обчислень, проводити так звану усну лічбу. Матеріал для цього етапу уроку вчитель запозичує з підручника, а також із спеціальних збірників усних задач і вправ.
Щоб навички усних обчислень постійно вдосконалювались, треба встановити правильне співвідношення в застосуванні усних і письмових прийомів обчислень, а саме обчислювати письмово тільки тоді, коли усно обчислити важко [29, 56].
Прийоми як усних, так і письмових обчислень ґрунтуються на знанні нумерації, конкретного змісту і властивостей арифметичних дій, зв’язку між результатами та компонентами дій, а також на знанні зміни результатів дій залежно від зміни одного з компонентів. Проте між прийомами усних і письмових обчислень є істотні відмінності [9]:
1)Усні обчислення виконують, починаючи з одиниць вищого розряду, а письмові – з нижчого (винятком є ділення). Наприклад:
450 + 120 = (400 + 50) + + 357
+ (100 + 20) = (400 + 100) + 246
+ (50 + 20) = 500 + 70 = 570 603
Обчислення виконано усно; Обчислення виконано письмово;
його виконують, починаючи його виконують, починаючи з з одиниць вищого розряду. одиниць нижчого розряду.
2) Проміжні результати під час усних обчислень зберігають у пам’яті, під час письмових – відразу записують.
3) Прийоми усних обчислень для тієї самої дії над парою чисел можуть бути різні залежно від особливостей прикладу і тієї властивості, яку використовують, а письмові обчислення виконують за точніше окресленим правилом, прийнятим для кожної арифметичної дій.
Наприклад:
48·15=48·(10+5)= 483
=48·10+48·5=480+ х
+240=720 15
48·15=48·(5·3)=48·5·3=
=240·3=720 2415
48·15=(40+8)·15=40·15+ 483
+8·15=600+120=720
Використовуються різні прийоми 7245 усних обчислень Використовується завжди той самий прийом письмового множення
4) Розв’язування під час усних обчислень записують у рядок (якщо це потрібно), а в письмових обчисленнях – стовпчиком .
5) Усні обчислення звичайно виконують над числами в межах 100 і над багатоцифровими числами, якщо обчислення над ними зводяться до випадків у межах 100, а письмово виконують дії над багато-цифровими числами тоді, коли усно обчислити важко.
|
Обчислювальні терміни вивчають у тісному зв’язку з розглядом певних питань теорії. Питання про місце введення обчислювальних прийомів та методику їх вивчення розглянуто у відповідних концентрах.
Виховуючи любов до усних вправ, вчитель допомагає учням активно працювати з навчальним матеріалом, пробуджує у них прагнення удосконалювати способи обчислень і розв’язування задач, менш раціональні замінювати досконалішими та економнішими. А це – важлива умова свідомого засвоєння матеріалу. Спрямованість мислительної діяльності на пошук раціональних шляхів розв’язання проблеми свідчить про варіативність мислення [19, 57].
Розв’язуючи певну задачу, обчислюючи вираз, учень повинен уважно розглянути умову завдання, зуміти помітити всі його особливості і в кожному конкретному випадку обрати ті шляхи, які простіше й швидше приводять до мети. Таким чином, при виконанні усних обчислень можна говорити про критичність мислення, тобто уміння оцінити запропоновані варіанти розв’язання і обрати більш раціональний підхід до виконання даного завдання.
Усні вправи також сприяють розвитку мовлення учнів, якщо з самого початку навчання вводити в тексти завдань і використовувати при обговоренні вправ математичні терміни. Навички правильного, точного і лаконічного мовлення, що формуються на уроках математики, позитивно впливають на загальну мовленнєву культуру. Важливо, щоб вчитель сам слідкував за своїм мовленням і формулював завдання ясно, чітко, лаконічно і послідовно.
Навички усних обчислень формують у процесі виконання учнями різних вправ. Розглянемо основні види їх [9; 19; 29; 41 та ін.].
1. Знаходження значень математичних виразів. Для вправ пропонують у тій або іншій формі математичний вираз, треба знайти його значення. Ці вправи мають багато варіантів. Можна пропонувати числові математичні вирази і буквені (вираз із змінною), при цьому буквам надають числових значень і визначають числове значення знайденого виразу.
Наприклад:
1) Знайдіть різницю чисел 100 і 9.
2) Знайдіть значення виразу с – k , якщо с = 100, k = 9.
Вирази можна запропонувати в різній словесній формі: від 100 відняти 9; 100 мінус 9; зменшуване 100, від’ємник 9, знайти різницю; знайти різницю чисел 100 і 9; зменшити 100 на 9 і т.д. Ці формулювання використовує не тільки вчитель, а й учні.
Вирази можуть бути на одну і більш як на одну дію. Вирази з кількома діями можуть містити дії одного ступеня або різних ступенів, наприклад: 47 + 24 - 56, 72 : 12 · 9, 400 – 70 · 4 тощо; можуть бути з дужками або без дужок: (90 - 42) : 3, 90 – 42 : 3.
Як і вирази на одну дію, вирази на кілька дій мають різне словесне формулювання, наприклад: від 90 відняти частку чисел 42 і 3; зменшуване 90, а від’ємник виражений часткою чисел 42 і 3 та ін.
Вирази можуть бути задані в різній області чисел: з одноцифровими числами (7 - 4), з двоцифровими (70 - 40, 72 - 48), з трицифровими (700 - 400, 720 - 480) і т.д., з абстрактними та іменованими числами (200 - 15, 2м –15см). Однак, як правило, прийоми усних обчислень повинні зводитися до дій над числами в межах 100. Так випадок віднімання чотирицифрових чисел 7200 - 4800 зводиться до віднімання двоцифрових чисел (72сот. - 48сот.), отже, його можна давати для усних обчислень.
Вираз можна дати у формі прикладу (усно або у вигляді запису): 7+2, 30 – 24 : 6, А можна дати і в інших формах, наприклад у формі таблиці:
| Зменшуване | 12 | 14 | 15 | 17 | 20 | 28 |
| Від’ємник | 10 | 10 | 10 | 10 | 10 | 10 |
| Різниця |
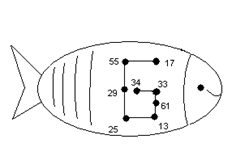
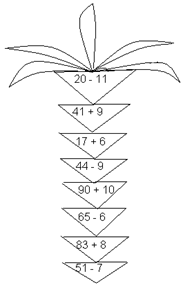
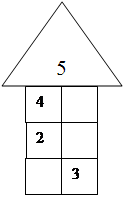
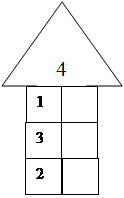
У 1 класі для цієї мети можна використати цікаві фігури.
Завдання на знаходження значень виразів можна безпосередньо пов’язувати з різними питаннями початкового курсу математики: з нумерацією, величинами, дробами тощо. Наприклад, знайти різницю найменшого трицифрового числа і найбільшого одноцифрового; знайти, скільки сантиметрів в 1/5м тощо.
Основне призначення вправ на знаходження значень виразів – виробити в учнів міцні обчислювальні навички. Водночас вправи на знаходження значень виразів сприяють і засвоєнню питань теорії арифметичних дій.
2. Порівняння математичних виразів. Ці вправи мають варіанти. Можна взяти два вирази і встановити, чи рівні їхні значення, а якщо не рівні, то яке з них більше чи менше. Наприклад, треба порівняти вирази і замість зірочок поставити знак ,,>“, ,,<“ або ,,=“ :
6 + 4 * 4 + 6 20 + 7 * 20 + 5
20 · 8 * 1 8 · 10 8 · 9 + 8 * 8 · 10
При цьому знак відношення можна вибрати на основі або знаходження значень даних виразів і порівняння їх (20·8<18·10, оскільки 160 < 180), або застосування відповідних знань: переставної властивості додавання (6 + 4 = 4 + 6), зміни результатів дій залежно від зміни одного з компонентів (20 + 7 > 20 + 5) тощо.
Можна запропонувати вправи, які вже мають знак відношення і один із виразів, а другий вираз треба скласти або доповнити. Наприклад, треба закінчити запис: 8 · (10 + 2) = 8 · 10 + …
Можна пропонувати вправи на порівняння виразів із змінною, наприклад, замість зірочки треба поставити знак ,,>“, ,,<“ або ,,=“, наприклад: а – 17 х а - 12.
Вирази в таких вправах можуть включати різний числовий матеріал: одноцифрові, двоцифрові, трицифрові числа і т. д.; абстрактні та іменовані числа. Вирази можуть бути з різними діями. Основне завдання таких вправ – сприяти засвоєнню теоретичних знань про арифметичні дії, їх властивості, рівності, нерівності тощо. Крім того, вправи на порівняння виразів допомагають і виробленню обчислювальних навичок.
Похожие работы
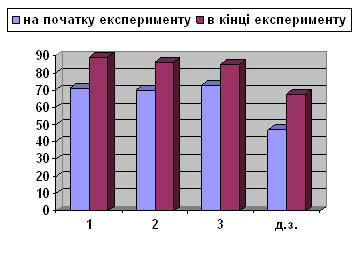
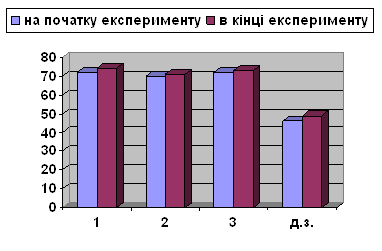
... 2 А клас (експериментальний клас) Правильно виконали (у %) № завдання Діаграма 2. 2 Б клас (контрольний клас) Правильно виконали (у %) № завдання Аналізуючи одержані результати експериментального дослідження можна зробити висновок, що дидактична гра – це ефективний метод навчання математики молодших школярів. Ігри та ігрові ситуації допомагають учням у навчанні, органі ...
... , пізнає щось нове, засвоює краще матеріал уроку тощо. Таким чином, проведений аналіз засвідчує, що і в практиці початкової школи, і в навчальній та методичній літературі проблема використання дидактичних ігор на уроках математики має певне відображення. Разом з тим, є і можливості, і потреби до більш глибокої розробки різних сторін цієї проблеми. Цей висновок підтверджує доцільність вибору теми ...
... міркувати, що зробило позитивний вплив на процес роботи над обчислювальними прийомами і навиками Висновки Експериментальна робота дає можливість сформулювати теоретичні висновки і практичні рекомендації щодо організації самостійної роботи учнів початкових класів. Аналіз психолого-педагогічної літератури засвідчив, що самостійна робота - це сукупність дій учня з предметами у певних умовах, що ...
... включення в ситуацію задач, задач-розповідей, завдань героїв веселих датських казок, включення задач-жартів, шляхом створення ігрових ситуацій та веселих змагань. 1.4 ігри на заняттях з математики. В позакласній роботі з математики з молодшими учнями велике місце займають ігри. Це головним чином дидактичні ігри, тобто ігри, зміст яких допомагає розвитку окремих операцій на мислення або засвоє ...
0 комментариев