Сутність та роль усних обчислень у початковому курсі математики
Види вправ для усних обчислень
Розв’язування рівнянь. Як усні вправи пропонують рівняння. Це насамперед найпростіші рівняння (х+2=10) і складніші (15·х- - 9 = 51)
Шляхи вдосконалення навичок усних обчислень у молодших школярів
Гра "Мовчанка" (рис. 2)
Зовнішні умови, що визначаються суспільними засобами життє-діяльності людини. Ці джерела активності називають спонуканнями [53, 42]
Методика експериментального дослідження
Дидактичні ігри
Аналіз результатів експериментального дослідження
Навигация
Зовнішні умови, що визначаються суспільними засобами життє-діяльності людини. Ці джерела активності називають спонуканнями [53, 42]
Усні обчислення на уроках математики в початкових класах
111696
знаков
4
таблицы
10
изображений
2. Зовнішні умови, що визначаються суспільними засобами життє-діяльності людини. Ці джерела активності називають спонуканнями [53, 42].
Методика проведення сучасного уроку передбачає додержання принципу тісного зв'язку навчання з життям. Уся навчально-виховна діяльність учителя при цьому спрямована на оптимізацію пізнавальної діяльності учнів. Під оптимізацією пізнавальної діяльності учнів розуміють таку організацію процесу засвоєння знань, в результаті якої учні в основному на уроці оволодівають знаннями, способами дій, соціально значимою ціннісною орієнтацією в навколишній дійсності, вчаться застосовувати здобуті знання на практиці. Усі зазначені аспекти діяльності учня на уроці мають перебувати у постійній взаємодії та взаємозв'язку, а це забезпечується комплексним підходом до створення навчальних ситуацій на уроці.
Комплексним підходом до розробки і створення навчальних ситуацій на уроці передбачається диференційована постановка навчальних завдань, керування процесом опанування учнями певного обсягу знань, організації їхньої самостійної мислительної діяльності. Звичайно, це не означає, що на кожному уроці мають виявлятись усі аспекти діяльності учнів. Ідеться про те, що коли на одному уроці навчальні ситуації спрямовувались на оволодіння певними знаннями, то на наступному уроці слід передбачати ситуації, які б стимулювали дослідницький пошук учнів чи сприяли організації їхньої самостійної мислительної діяльності [60, 49].
Виявом пізнавальної активності є бажання учнів ставити запитання, що виникають в процесі засвоєння навчального матеріалу. Учитель може спрямовувати запитання учнів на встановлення зв'язку між змістом навчального матеріалу і тією інформацією, яку вони здобувають з різних джерел (радіо, телебачення, додаткова література). Так, при вивченні усного додавання і віднімання багатоцифрових чисел учні можуть цікавитись відстанню від Землі до інших планет чи швидкістю космічного корабля. Після засвоєння теми «Площа» в учнів виникають запитання, пов'язані з їхнім досвідом, вони зацікавлюються тим, як обчислити площу різних навколишніх об'єктів [45, 53].
Отже, при створенні навчальних ситуацій на уроках не слід обмежуватися лише вимогами і завданнями підручника. Корисно пропонувати учням завдання і ставити вимоги, які б змушували їх проводити самостійні дослідження. Наприклад, щоб розкрити зв'язок між додаванням І відніманням, учням корисно запропонувати завдання (крім тих, що вміщені у підручнику) такого типу:
1. Скласти задачу, розв'язування якої розкривало б зв'язок віднімання з додаванням.
Зразок задачі: Скільки метрів тканини залишилося в куску завдовжки 30 м, якщо із 17 м цієї тканини пошили костюми?
Розв’язати її додаванням і відніманням.
30—17=13.
2. Дізнатися, чому число, від якого віднімали в першому прикладі, дорівнює числу, яке є результатом другого прикладу.
1) 33—17=16;
2) 16+17 = 33.
Подібні завдання можуть використовуватись на різних етапах уроку. Виконуючи їх, учні повинні усвідомити, що між діями додавання і віднімання закономірно існує зв'язок; результат дії додавання можна перевірити дією віднімання і навпаки.
У навчальних ситуаціях, що створюються на уроці, реалізується певна система взаємодій вчителя і учнів. Головна їх мета не лише засвоєння програмного навчального матеріалу, а й оволодіння уміннями застосовувати здобуті знання на практиці.
Оптимізацією діяльності учнів передбачається створення системи навчальних ситуацій, спрямованих на формування в учнів прийомів розумової діяльності. Учні під час виконання навчальних завдань вчаться спостерігати, запам'ятовувати, класифікувати й узагальнювати ознаки об'єктів [16, 23].
Навчальні ситуації уроку, які сприяють формуванню прийомів розумової діяльності, різні як за своїм змістом, так і за функціями. Джерела виникнення їх також неоднакові. Одні з них спеціально розробляються вчителем, інші — виникають стихійно. Деякі ситуації виникають у процесі діяльності вчителя, інші — зумовлюються діяльністю учнів. Одні ситуації, що виникають на уроці, сприяють засвоєнню учнями практичних дій, інші — викликають у них потребу виконувати розумові дії.
Спостережливість учнів розвивається різними прийомами організації сприймання: спрямуванням їх на розв'язування задач різного типу, на виконання підготовчих вправ, на практичне оперування навчальним матеріалом, на розв'язування задач з обов'язковим порівнянням їх змісту і плану розв'язування [38, 167].
Для організації сприймання навчального матеріалу учнями і формування в них спостережливості недостатньо використовувати на уроці різний за змістом і формою дидактичний матеріал. При розробці навчальних ситуацій уроку потрібно враховувати набутий життєвий досвід і знання учнів, спеціально спрямовувати їх на виділення основних властивостей об'єктів навчального матеріалу, зокрема тих, що потрібні їм для засвоєння наступних знань і що можуть застосовуватись у практичній діяльності. Важливою вимогою в організації спостережливості учнів є постановка конкретного завдання. Наприклад: навчитися на уроці розрізняти прийоми усного обчислення дій додавання і множення, дізнатися, якими способами можна швидше обчислювати, множення числа на суму.
Створити навчальні ситуації, що сприяють формуванню спостереж-ливості учнів, можна за допомогою завдань типу:
1. У дворі гралося 7 дівчаток. З будинку вийшла ще одна дівчинка — Оленка. Якою вона буде по рахунку?
2. У дворі гралося 7 дівчаток. З будинку вийшла ще одна дівчинка. Скільки дівчаток стало гратися у дворі?
3. У дворі гралося 7 дівчаток. У будинок зайшла одна дівчинка. Скільки дівчаток залишилось гратися в дворі?
Чим відрізняються задачі одна від одної?
Для формування уважності в учнів використовуються такі можливості уроку, як розповідь вчителя щодо раціонального способу виконання завдань, користування паузами, різні форми подачі навчального матеріалу, контрастність у створенні навчальних ситуацій та в організації діяльності учнів. Важливо, щоб перед кожним етапом пояснення матеріалу і після нього вчитель робив невеликі паузи. Потрібні паузи і перед розкриттям змісту навчального матеріалу, визначенням основних ознак об'єкта, що вивчається. Паузи роблять для того, щоб учні змогли зосередитись, переключитись з одного виду завдань на інший, змінити установку.
Обов'язковою вимогою до організації уваги учнів є використання вчителем елементів новизни в формі подачі знань, в їх змісті, у звичній для учнів діяльності на уроці. Важливим є додержання контрастності у зовнішніх впливах [53, 43].
Розглянемо ситуацію, яка створюється на уроці для формування спостережливості, уважності і довільного запам'ятовування школярів.
Під час ознайомлення з прийомами усного множення і ділення на 5 учням пропонується набір чисел
240 70 370
460 90 560
720 120 790
і такі запитання та завдання:
На яке число швидко можна поділити ці числа? (Відповідь: на 10.)
Чи можна швидко поділити ці числа на 5? (Швидко не можна поділити.)
Для цього треба порівняти числа І0 і 5. Що про них можна сказати? (Число 5 менше від 10 в два рази.)
Коли дільник зменшити в 2 рази, то що станеться з часткою? (Частка зменшиться вдвічі).
Перевірте, чи правильна буде частка. (240 : 10 = =24,240:5=48.)
Як 240 можна легко поділити на 5? (240: 10-2 = 48.)
Яке правило можна сформулювати про ділення числа на 5?
(Щоб поділити число на 5, треба поділити його на 10 і результат помножити на 2.)
Розвитку мислення учнів на уроці сприяють навчальні ситуації, в яких учні опиняються перед необхідністю досліджувати об'єкт, розкривати певні закономірності, встановлювати раціональний спосіб розв'язування задачі, складати систему задач тощо. Для таких ситуацій доцільно використовувати текстові задачі, в яких дані величини зображуються різного роду символікою (буквами, цифрами, фігурами), реальними предметами; задачі в прямій і непрямій формі, із зайвими і недостатніми даними [50, 74].
Ситуації, в яких учні переформульовують завдання, сприяють виробленню в них уміння оцінювати власну діяльність. Наприклад, у завданні потрібно дізнатись, на скільки число 33 більше від 19. Учням повинні замінити цю вимогу аналогічною їй:
Яке число треба додати до 19, щоб дістати 33? Чому дорівнює різниця чисел 33 і 19?
Нехай, наприклад, дано задачу:
У селі 210 цегляних будинків, а дерев'яних на 70 менше. Скільки будинків у селі?
Учні формулюють її по-іншому:
Різниця між кількістю цегляних і дерев'яних будинків у селі дорівнює 70. Цегляних будинків 210. Скільки будинків дерев'яних?
Учні, переформульовуючи в думці умови і вимоги завдань, поглиблено аналізують їх зміст.
Наприклад, розглядаючи запис 26—15, вони роблять такі висновки:
Цей математичний вираз є різницею чисел 26 і 15; такий запис означає, що потрібно знайти значення виразу. Воно дорівнює числу 11. Число 11 є різницею чисел 26 і 15. Воно означає, що 26>15 на 11, або що 15<25 на її. Числа 15 і 11 в сумі дають 26. Число 26 — зменшуване, а число 15 — від'ємник.
Засобом спрямування мислительної діяльності учнів на пошук істотних ознак способу виконання завдання є певним чином сформульовані запитання вчителя до учнів після виконання ними запропонованого завдання.
Наприклад, учням пропонується виконати завдання такого типу:
Сума трьох доданків дорівнює 100. Перший доданок 40, третій 35. Чому дорівнює другий доданок?
Учні аналізують зміст завдання. Основним предметом їхнього аналізу є зв'язок між першим і третім доданками та сумою трьох доданків. Щоб розкрити зв'язок між зазначеними об'єктами, потрібно було поставити і виконати завдання, яке не пропонувалося в умові завдання і не було його вимогою. Справді, у завданні ставилася вимога знайти другий доданок і не наголошувалось, що для цього достатньо знайти суму першого і третього доданків. Потреба у виконанні цієї дії виникла в результаті характеристики змісту. Інакше кажучи, нове, що випливає з даного завдання, є результатом проведеного учнями аналізу змісту завдання через синтез. Таким чином, постановка і виконання вихідного завдання має важливе значення в пошуках способу виконання завдання. Щоб учні переконалися в правильності знайденого ними способу виконання завдання, учитель, після того як вони виконають завдання, запитує в них про те, що насамперед привернуло їхню увагу в завданні, про що треба було дізнатися, щоб виконати завдання,, як перевірялась правильність поставлених ними завдань.
Похожие работы
... 2 А клас (експериментальний клас) Правильно виконали (у %) № завдання Діаграма 2. 2 Б клас (контрольний клас) Правильно виконали (у %) № завдання Аналізуючи одержані результати експериментального дослідження можна зробити висновок, що дидактична гра – це ефективний метод навчання математики молодших школярів. Ігри та ігрові ситуації допомагають учням у навчанні, органі ...
... , пізнає щось нове, засвоює краще матеріал уроку тощо. Таким чином, проведений аналіз засвідчує, що і в практиці початкової школи, і в навчальній та методичній літературі проблема використання дидактичних ігор на уроках математики має певне відображення. Разом з тим, є і можливості, і потреби до більш глибокої розробки різних сторін цієї проблеми. Цей висновок підтверджує доцільність вибору теми ...
... міркувати, що зробило позитивний вплив на процес роботи над обчислювальними прийомами і навиками Висновки Експериментальна робота дає можливість сформулювати теоретичні висновки і практичні рекомендації щодо організації самостійної роботи учнів початкових класів. Аналіз психолого-педагогічної літератури засвідчив, що самостійна робота - це сукупність дій учня з предметами у певних умовах, що ...
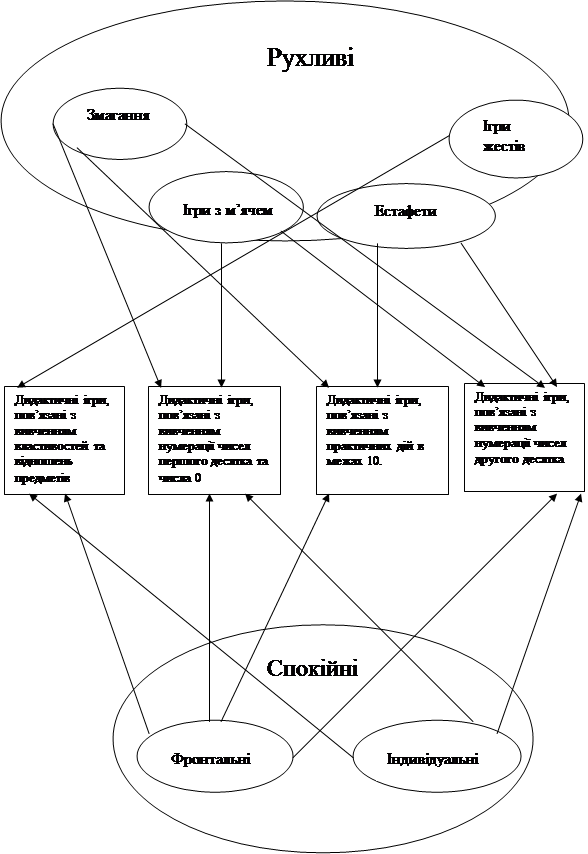
... включення в ситуацію задач, задач-розповідей, завдань героїв веселих датських казок, включення задач-жартів, шляхом створення ігрових ситуацій та веселих змагань. 1.4 ігри на заняттях з математики. В позакласній роботі з математики з молодшими учнями велике місце займають ігри. Це головним чином дидактичні ігри, тобто ігри, зміст яких допомагає розвитку окремих операцій на мислення або засвоє ...
0 комментариев