Навигация
Групова форма
3. Групова форма
Групи учнів не постійні, їх кількісний і якісний склад може здійснюватися залежно від рівня досягнень учнів, змісту теми тощо. Об’єднуючи учнів у групи, вчитель одержує можливість організувати навчання різне за змістом, рівнем складності, обсягом завдань, тобто враховує індивідуальні запити школярів за певних умов.
При диференціації учителю необхідно:
- враховувати загальну готовність учнів до наступної діяльності;
- передбачати труднощі, які можуть виникнути в учнів під час засвоєння матеріалу;
- використовувати диференційовані завдання індивідуального та групового характеру в системі уроків;
- проводити перспективний аналіз діяльності власної і учнів: з якою метою планується виконання тих чи інших завдань, чому їх треба виконувати саме на даному етапі уроку, як продовжити розпочату роботу на наступних уроках.
а) Парна
1. Поставити один одному такі запитання:
- Що в задачі відомо про …?
- Що запитується в задачі?
- Скількома діями можна розв’язати задачу?
Мета: розвиток умінь опрацювати зміст задачі.
2. Перевірити один одного, чи правильно зрозумів задачу, а потім удвох обміркувати план її розв’язання.
Один учень називає запитання плану, а другий – дії, що треба виконати.
Мета: розвиток умінь знаходити і обговорювати план розв’язання задачі.
3. Розв’язати задачу самостійно, а потім зробити взаємоперевірку.
Мета: розвиток умінь контролювати правильність ходу розв’язання задачі.
б) Ланкова (діяльність постійних груп учнів) тривалість роботи 5 – 10 хвилин протягом уроку.
1) 4 задачі різного типу. Кожен учень бере задачу, яку дає ланковий, витягнувши з конверта.
2) Задачі для ланок дублюються.
3) Для однієї ланки лише 2 задачі.
4) Для однієї ланки 1 задача. Кожна ланка має задачі різного типу.
в) Диференційовано-групова. 3 групи – сильніша, середня і слабка. Для слабкої групи дається підказка.
Отже, готуючи диференційовані завдання, вчитель обов’язково зіставляє їх мету й зміст з рівнем знань і розвитку учнів, шукає те спільне в змісті й характері завдань, без чого не можна правильно визначити ступінь їх складності для кожної групи, і на цій основі визначає необхідний і посильний зміст та обсяг роботи. Лише за таких умов створюються сприятливі можливості для успішного навчання кожної дитини.
2.2 Організація і зміст експериментального дослідження
Дипломне дослідження мало теоретико-експериментальний характер і проводилося у два етапи. На теоретичному етапі (І семестр) була визначена сфера і проблема дослідження; вивчалася педагогічно-психологічна, методична література з даної теми; аналізувалася робота вчителів початкових класів у галузі методики розв’язування текстових задач в процесі диференційованої роботи; формулювалася гіпотеза та завдання дослідження.
В процесі експериментального етапу (ІІ семестр) – на основі напрацьованої теоретичної інформації здійснювався формуючий експеримент, пов’язаний із формуванням у молодших школярів умінь і навичок розв’язування текстових задач в процесі диференційованого підходу, вивчалася його ефективність та практична значущість.
Формуючий експеримент здійснювався за такими етапами:
· власне формуючий експеримент, в процесі якого пропонувалася добірка диференційованих завдань і проводилася систематична цілеспрямована робота із формування відповідних навичок та вмінь з використанням диференційованого підходу;
· теоретико-узагальнюючий – основна увага спрямовувалася на теоретичний аналіз і узагальнення результатів формуючого експерименту, оформлення роботи та з’ясування подальших перспектив розробленої добірки завдань.
Експериментальне дослідження ми проводили у загальноосвітній школі І–ІІІ ступенів с. Буцнів, Тернопільського району, Тернопільської області. Ним було охоплено 23 учні 4-а класу (експериментального) і 21 учень 4-б класу (контрольного). У процесі формуючого експерименту ми пропонували четвертокласникам добірку завдань, диференційованих за складністю і спрямованих на вироблення вмінь розв’язувати текстові задачі в початковій школі. Ці завдання використовувалися як на уроках, так і на позакласних заняттях з математики і для самостійної роботи учнів.
Проаналізувавши результати роботи у 4–а класі протягом вересня - листопада, ми побачили, що в середньому в класі більш-менш постійно працювали з диференційованими завданнями всі учні експериментального класу. Учитель фіксував, як кожен учень справляється із диференційованим завданням: повністю, частково чи зовсім не справлялися. Виявилося, що в переважній більшості випадків із завданнями ІІ рівня справлялися лише 5 – 6 учнів. У наступних місяцях ці показники дещо покращилися. В кінці І семестру учитель провів контрольну роботу, в якій було 3 обов’язкові і одне необов’язкове завдання – задача «із зірочкою». Цю задачу бралися розв’язувати 10 учнів (із 14 учнів класу), але розв’язало її 8 учнів. Спостерігаючи за роботою класу, ми виявили зростання інтересу учнів до диференційованих завдань. З’явилася група учнів, яка самостійно справлялася з більшістю додаткових завдань.
Аналогічні дослідження були проведені і в 4 –б класі. Протягом першого семестру серед учнів цього класу теж виділилася група сильніших учнів, які працювали із диференційованими завданнями. Було помічено деякі відмінності у роботі учнів при диференційованому підході розв’язувати текстові задачі.
Аналізуючи завдання, які не міг розв’язати жоден учень, і завдання, з якими деякі учні справлялися частково, ми зіткнулися з потребою з’ясувати питання про форми організації роботи над диференційованими завданнями: фронтальну, індивідуальну, групову і методику їх використання. Вивчаючи причини, через які на багатьох уроках не знайшлося часу для запланованих учителем текстових задач, ми дійшли до потреби дослідити особливості використання диференційованих завдань на різних етапах уроку. Було визначено також, які конкретні види диференційованих завдань потребували спеціальної експериментальної роботи щодо методики їх опрацювання. Таким чином, було визначено, що самої добірки диференційованих завдань недостатньо для того, щоб дістати видимі зрушення у розумовій діяльності молодших школярів. Щоб добірка завдань ефективно функціонувала, потрібно дати вчителям методику використання диференційованого підходу при навчанні учнів розв’язуванню текстових задач.
Методика формуючого експерименту включала проведення спеціально розроблених уроків і їх фрагментів та окремих позаурочних занять; безпосереднє проведення занять самим дослідником; спостереження за діями вчителя і учнів у процесі роботи диференційованим підходом при розв’язуванні текстових задач.; анкетування та аналіз усних відповідей і письмових контрольних робіт учнів; проведення бесід з учителями і учнями про розв’язування текстових задач експериментальної системи.
Результативність дослідження оцінювалася на основі виконання учнями диференційованих завдань при розв’язуванні текстових задач, частково використовувалося порівняння результатів початкового і кінцевого зрізів, а також бесід з учителями та безпосередніх спостережень.
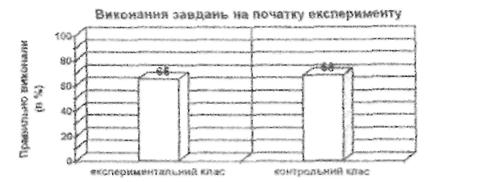
У ході першого етапу експерименту була проведена контрольна робота, яка проводилася в експериментальному та контрольному класах на початку жовтня, після завершення етапу повторення навчального матеріалу за минулий рік.
Результати цієї контрольної роботи узагальнено в таблиці 2.1.
Виконання програмових і диференційованих завдань
На початку року в контрольних та експериментальних класах
| Правильно розв’язали (у %) | ||||
| Класи | 1-е програмове завдання | 2-е програмове завдання | 1-е Диференційоване завдання | 2-е Диференційоване завдання |
| 4-б контр. | 75 | 76 | 75 | 76 |
| 4-а експер. | 72 | 71 | 71 | 73 |
З таблиці видно, що результати цієї контрольної роботи приблизно однакові і в контрольному, і в експериментальному класах.
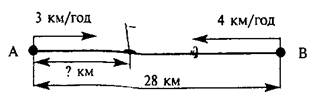
У ході формуючого експерименту були виявлені труднощі, які виникають в учнів при розв’язуванні текстових задач. Так, учням 4-б класу важко давалося розв’язання задачі № 860 (4 клас) «Літаку потрібно було пролетіти 4500 км. Перші 3 год він летів зі швидкістю 695 км/год, а наступні 2 год – зі швидкістю 642 км/год. Скільки кілометрів йому залишилося пролетіти?» Цю задачу більшість дітей не розв’язала. У подібних випадках рекомендується вчителю при розв’язуванні текстових задач застосовувати диференційований підхід.
Краще діти справлялися із текстовими задачами, якщо вчитель використовував багаторазове пояснення. Зауважимо, що лише сильні учні класу обходилися без допомоги при розв’язуванню текстових задач. Інші ж учні нерідко мали труднощі в самостійній роботі при розв’язуванню текстових задач, тому робота з середніми учнями на уроці здебільшого була можлива лише у фронтальній формі.
Ми враховували, що перехід від оцих найпростіших, підготовчих завдань до більш складних має бути добре продуманим і вмотивованим психологічно. Адже дуже легко переступити ту грань, за якою учні зневіряться у власних силах і втратять бажання працювати над розв’язанням текстових задач. Тому ми й пропонуємо своєрідний проміжний варіант: школярі розв'язують завдання водночас і самостійно, і за підказкою вчителя. Обсяг такої підказки міг бути різним:
1.Розглянь розв'язування задачі і розв'яжи аналогічну.
2.За зразком розв'язування задачі склади аналогічну і розв'яжи її.
3.Розв'яжи задачу за поданим планом і поміркуй, чи можна знайти результат іншим способом.
4.Самостійно розв'яжи задачу... (вказується, яким способом).
5.Закінчи розв'язування задачі. (Вказано перші кроки).
Наведемо приклад підказки.
Задача.
Якщо шматок дроту розрізати на 4 частини по 16 м у кожній, то залишиться ще 6 м. однак дріт розрізали на частини по 5 м у кожній. На скільки частин розрізали дріт?
Аналіз. Щоб знайти відповідь, треба знайти довжину всього шматка дроту. Знайдемо довжину за першою частиною умови. Залишилося 6 м. отже, потрібно ще знайти, скільки метрів дроту розрізали на 4 частини.
Закінчи аналіз задачі, склади план її розв’язування і запиши розв’язання. Зразок розв’язування. На картці подано дві задачі одного виду, одна з яких вже розв’язана.
1. Доярка надоїла 9 л молока. 16 л вона віддала телятам, а решту розлила порівну в 4 бідони. Скільки літрів молока доярка налила в один бідон?
1) 96 – 16 = 80 (л);
2) 80 : 4 = 20 (л).
Відповідь. 20 літрів.
2. Виготовили 40 л томатного соку. 13 л соку вилили в сулію, а решту розлили порівну в 9 банок. Скільки літрів соку налили в одну банку?
Перевірити розв’язання першої задачі та розв’язати другу. Подання пояснення чи плану розв’язання задачі.
Інколи учителю важко було скласти картку з допомогою, особливо коли ця допомога була диференційованою. В цьому випадку до однієї і тієї ж задачі потрібно було зробити 3 картки. Одну дати сильному учневі, другу дати середньому, а третю – слабкому учневі.
Наведемо приклад диференціації на трьох картках.
Літаку потрібно було пролетіти 4500 км. Перші 3 год він летів зі швидкістю 695 км/год, а наступні 2 год – зі швидкістю 642 км/год. Скільки кілометрів йому залишилося пролетіти?
Картка 1
1. Прочитай задачу.
2. Розглянь графічний малюнок до неї.
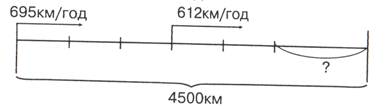
3. Розв’яжи задачу, добираючи відповідні дії.
1) _____________________ - пролетів літак за 3 год;
2) _____________________ - пролетів літак за 2 год;
3) _____________________ - всього пролетів літак;
4) _____________________ - залишилося пролетіти.
4. Запиши відповідь і зроби перевірку за схемою.
1 + 1 + 1 = 4500 (км)
Картка 2
1. Прочитай задачу.
2. Склади план і розв’яжи задачу.
3. Запиши відповідь.
Картка 3
1. Прочитай задачу.
2. Склади числовий вираз і розв’яжи задачу.
3. Запиши відповідь.
Додаткове завдання
1. Обчисли, на скільки менше відстані залишилося пролетіти, ніж він пролетів.
2. Запиши відповідь
У ході експерименту порівняння ефективності навчання в експериментальному та контрольному класах здійснювалося за такими показниками:
1) за результатами засвоєння основного матеріалу програми з математики для початкових класів;
2) за змінами в загальному розвитку дітей, їхніх інтересах, ставленні до навчання.
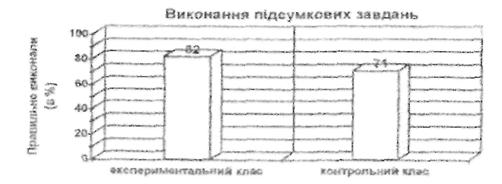
У квітні місяці в експериментальному і контрольному класах були проведені контрольні роботи. Перше, друге та третє завдання стосувалося суто програмового матеріалу, четверте не виходило за межі програми, але мало певні ускладнення у формулюванні.
Наведемо приклади цього завдання і результати його виконання.
? Розв’яжи задачу за допомогою рівняння.
У магазин привезли 154 пари взуття. Через п’ять днів залишилося 87 пар. Скільки пар взуття продали протягом п’яти днів?
Виконання підсумкових програмових завдань (квітень)
В експериментальному і контрольному класах
| Правильно розв’язали (у відсотках) | ||
| Класи | 1- 2 е завдання | 3-е завдання |
| 4-б контрольний | 76 | 77 |
| 4-а експерим. | 80 | 83 |
Виконання додаткових завдань в експериментальному
і контрольному класах
| Правильно розв’язали (у відсотках) | |
| Класи | 4-е завдання |
| 4-б контрольний | 77 |
| 4-а експерим. | 82 |
Порівняння наслідків виконання контрольної роботи свідчить про те, що в експериментальному класі рівень умінь розв’язувати текстові задачі, застосовуючи диференційований підхід, значно вищий, ніж у контрольному, причому особливо відрізняються результати розв’язання додаткового завдання. Ми пояснюємо це цілеспрямованою роботою диференційованого підходу у процесі навчання молодших школярів розв’язувати текстові задачі, яка проводилася відповідно до завдань формуючого експерименту, що привело до позитивних зрушень у розвитку мислення школярів.
Похожие работы
... правильність результатів; показувати, до яких негативних результатів можуть привести допущені в розв'язанні задачі помилки. Розглянемо прийоми перевірки правильності розв'язування задач та питання методики формування у молодших школярі" уміння застосовувати їх. У 1-4 класах доцільно поступово запроваджувати такі прийоми перевірки; порівняння результату, який дістати учні в процесі розв'язання ...
... школярів математичних уявлень і понять. Усвідомлення їх є важливим як для практично-життєвої підготовки учнів, так і для подальшого засвоєння математичних знань у середніх класах. 1.2 Проблема формування вмінь у другокласників розв’язувати складені задачі Традиційно ознайомлення з поняттям “складена задача” здійснюється в 2-му класі на задачах на знаходження остачі, й ці задачі пропонуються ...
... робити схеми аналітичного або синтетичного способу розбору задач, хоча це не належить до обов'язкових умінь, наведених у програмі з математики для 1–4 класів. 2. Формування умінь учнів розв’язувати задачі на рух 2.1 Аналіз системи задач на рух у початковому курсі математики Вивчення всіх питань програми з математики пов'язане з розв'язуванням арифметичних задач. З одного боку, вони є ...
... -наслідкові зв’язки, зробити узагальнення і висновки. Результати формуючого експерименту свідчать, що використання удосконаленої методики позитивно вплинуло на розвиток умінь і навичок учнів експериментального класу розв'язувати задачі на пропорційне ділення. Таким чином, ми отримали результати, що підтвердили наше припущення: уміння і навички учнів експериментального класу розв’язувати задачі на ...


0 комментариев