Рационализация дробей: rationalize ()

8. Рационализация дробей: rationalize ()

Рационализация дроби – это избавление от иррациональности в знаменателе этой дроби. Команда rationalize () производит такое преобразование над числовыми и алгебраическими дробями. Причем в случае алгебраической дроби принимается во внимание только знаменатель в виде полинома. Эта команда может рационализировать алгебраическую дробь, знаменатель которой содержит трансцендентные функции типа sin (), ехр (), ln () и т.п. Однако если их аргумент является дробью с иррациональностями в знаменателе, то эти конструкции не участвуют в процессе рационализации.

Пример 11. Рационализация дробных выражений.

> a:=7*(3^(1/3)+4^(1/5))/(3–2^(1/3));

 

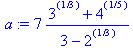
> rationalize(a);

 

> b:=y/(y+sqrt (2‑sqrt(5)));

 

> rationalize(b);

 

> c:=1/(3‑root (cos(1/(2+sqrt(mu))), 5));

 

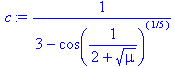
> rationalize(c);

 

 

9. Ограничения на неизвестные: assume ()

Часто в математических выводах приходится делать те или иные предположения относительно некоторых величин, фигурирующих в наших исследованиях, т.е. как-то ограничивать эти величины. Одни ограничения логически вытекают из области определения независимых переменных, входящих в выражения, другие мы накладываем сами. В системе Марlе имеются команды для введения и проверки ограничений, наложенных на некоторые неизвестные или даже целые выражения. Введенные ограничения используются командами и функциями Maple, например simplify(), sqrt(), для получения более простого ответа, если введенные ограничения позволяют это.

Назначение команды assume () – накладывать ограничения на неизвестные величины Maple. Команда имеет следующий синтаксис:

assume (x, свойство);

Здесь х – любая неопределенная переменная или выражение с такими переменными, а параметр свойство может принимать значения, равные названиям свойств (специальным символьным именам, зарезервированным Maple для задания различных ограничений на переменную или выражение, определенные первым параметром), имени типа данных и числовому диапазону. Некоторые из наиболее употребительных свойств перечислены в табл. 1.

Таблица 1. Свойства числовых переменных и выражений

Название свойства	Описание
negative	Отрицательные вещественные числа из интервала (-¥, 0) (нуль не включается)
nonnegative	Неотрицательные вещественные числа из интервала (0,¥) (нуль включается)
positive	Положительные вещественные числа из интервала (0,¥) (нуль не включается)
natural	Натуральные числа (целые, большие или равные 0)
posint	Целые строго большие 0
odd	Нечетные числа
even	Четные числа
complex	Комплексные числа
NumeralNonZero	Комплексные числа, исключая 0
real	Вещественные числа
rational	Рациональные числа (дроби и целые)
irrational	Иррациональные числа
integer	Целые числа
fraction	Только дробные числа
prime	Простые числа

Некоторые параметры (х, свойство) можно заменить математическим отношением, если, конечно, это возможно. Например, (x, negative) соответствует отношению х<0, а (х, nonnegative) соответствует х>=0 и т.д.

При наложении на переменную каких-либо ограничений в результатах выполнения действий над выражениями, в которые входит эта переменная, сразу же за ее именем по умолчанию отображается символ тильда (~). Эту функциональность по умолчанию можно изменить на следующие:

¨ либо вообще не информировать пользователя, что на переменную наложены ограничения, и она будет продолжать отображаться как и все переменные без ограничений (команда Options Þ Assumed Variables Þ No Annotation);

¨ либо в области вывода, если отображаются результаты, в которых присутствует переменная с наложенными ограничениями, словесно сообщается, на какие переменные наложены ограничения (команда Options Þ Assumed Variables Þ Phrase).

Пример 12. Способы отображения переменных с ограничениями.

> assume (a>0);

> ln (a^2); #Отображение по умолчанию

> ln (a^2); #Режим не информировать пользователя

> ln (a^2); #Словесное сообщение

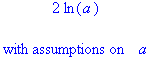
Вернуться в режим отображения переменных с наложенными ограничениями по умолчанию можно командой Options Þ Assumed Variables Þ Trailing Tildes.

В качестве своих параметров команда assume () может получать несколько пар (х, свойство) или несколько математических отношений. В этом случае все заданные ограничения действуют одновременно. Поэтому наложение ограничений в виде

> аssumе (х>3, х<5);

соответствует тому, что переменная х может изменяться только в интервале (3,5).

Новое ограничение, накладываемое новой командой assume () на переменную, отменяет все предыдущие ограничения. Поэтому последовательное задание ограничений двумя командами:

> assume (x>3);

> assume (x<5);

соответствует предположению, что значение переменной х не превосходит числа 5, а не тому, что значение этой переменной должно лежать в интервале (3,5).

Если необходимо еще добавить ограничения на переменную, то можно использовать команду additionally(), параметры которой полностью соответствуют параметрам команды assume (). Тогда ограничения, определенные командой additionally (), добавляются к ограничениям, введенным командой assume () и предыдущими командами additionally ():

> assume (x>3); # В последующих вычислениях предполагается х>3

(какие-то вычисления)

> аdditiоnаllу (х<=5); #Теперь предполагается, что 3<х<=5

Чтобы снять все ранее наложенные на переменную ограничения следует этой переменной просто присвоить ее же символьное имя (имя переменной, заключенное в одинарные кавычки). Для снятия всех ограничений переменной х предыдущих примеров, следует просто выполнить следующую операцию присваивания:

> x:='x';

Если же переменная с наложенными ограничениями использовалась в выражениях, то простое присваивание имени переменной самой переменной не снимает ограничения на переменную в этих выражениях. Подобная ситуация иллюстрируется в примере 13.

Пример 13. Снятие ограничений с переменной.

> assume (b>0);

> d:=surd (b^4,4);

 

> b:='b':b;

> d;

Как видим, снятие всех наложенных на переменную b ограничений не снимает, однако, этих ограничений с переменной b в выражении d. Чтобы снять ограничения с этой переменной, следует до команды снятия ограничений с переменной воспользоваться командой подстановки subs () и первым параметром указать замену переменной b на ее символьное имя 'b'.

Пример 14. Снятие ограничений с переменной в выражении.

> assume (b>0);

> d:=sqrt (b^4);

 

> d;

 

> d:=subs (b='b', d);

 

> b:='b';

 

> d;

 

Функция is () определяет, удовлетворяет ли некоторая переменная рабочего листа определенному свойству. Эта функция возвращает значение true, если все возможные значения переменной соответствуют заданному свойству. Если хотя бы одно из возможных значений не соответствует заданному свойству, то функция is () возвращает false. Функция is () может возвратить значение FAIL, что говорит о невозможности определить, соответствует или нет заданная переменная заданному свойству. Это бывает или в результате недостаточности информации относительно ограничений на переменную, или невозможности вычислить логические ограничения на переменную.

Пример 15. Удовлетворяет ли переменная заданным ограничениям.

> assume (a>0);

> is (a>0);

> is (a<1);

> additionally (a<1);

> is (a<1);

С помощью функции coulditbe () можно проверить, может ли заданная переменная соответствовать заданному свойству. Она возвращает true, если хотя бы одно из возможных значений переменной может иметь заданное свойство, и fа1sе в противном случае. Смысл значения FAIL соответствует такому же значению для функции is().

Пример 16. Может ли переменная удовлетворять заданным ограничениям.

> assume (a>0);

> is (a>0);

> coulditbe (a=1);

> additionally (a<1);

> coulditbe (a=1);

Команда about () отображает информацию о наложенных ограничениях на неизвестную величину:

> about(a);

Originally a, renamed a~:

is assumed to be: RealRange (Open(0), Open(1))

Как отмечалось ранее, многие функции и команды Maple используют информацию о наложенных на неизвестную величину ограничениях при выполнении символьных вычислений. Например, Марle не может вычислить следующий предел из-за неизвестности знака символьной переменной а:

> int (exp(a*x), x=0..infinity);

Definite integration: Can't determine if the integral is convergent.

Need to know the sign of –> – a

Will now try indefinite integration and then take limits.

Стоит предположить, что a>0, и Maple тут же вычислит данный интеграл, который он свел к вычислению предела, зависящего от параметра:

> assume (a>0);

> int (exp(a*x), x=0..infinity);

Литература

1. Говорухин В.Н., Цибулин В.Г. Введение в Maple. Математический пакет для всех. – М.: Мир, 1997. – 208 с.

2. Дьяконов В.П. Математическая система Maple V. – М.: Издательство «Солон», 1998.

3. Двайт Г.Б. Таблицы интегралов и другие математические формулы. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 176 с.

4. Матросов А.В. Maple 6. Решение задач высшей математики и механики. – СПб.:БХВ – Петербург, 2001. – 528 с.

5. Манзон Б.М. Maple V Power Edition – М.: Информационно-издательский дом «Филинъ», 1998 г.