Постановка задач расчета электромагнитного поля электротехнического устройства

1.1 Постановка задач расчета электромагнитного поля электротехнического устройства

Математическим описанием непрерывных в пространстве и во времени процессов электромагнитного поля в технических объектах и системах являются дифференциальные уравнения в частных производных (уравнения математической физики). Различают стационарные (не меняющиеся во времени) и нестационарные (переменные, меняющиеся во времени) процессы. Стационарные процессы описываются эллиптическими уравнениями, а нестационарные – уравнениями параболического и гиперболического типов.

Эти уравнения для электромагнитных полей относительно характеристик поля (векторов напряженности электрического и магнитного полей E и H ; векторов электрической и магнитной индукции D и B ; векторного магнитного потенциала A, скалярного электрического потенциала φ получают из преобразования уравнений Максвелла.

Наиболее часто используемые эллиптические уравнения – это уравнения Лапласа и Пуассона, которыми в теории электромагнетизма описываются задачи электростатики и магнитостатики. Простейшим эллиптическим уравнением является уравнение Лапласа:

 [1]

где лапласиан (оператор Лапласа) . Этот оператор может быть применен к скалярным и векторным функциям. В декартовой системе координат уравнение Лапласа имеет вид

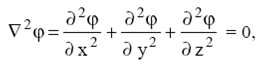[2]

где φ (x, y, z) – скалярная функция.

В цилиндрической системе координат оно выглядит следующим образом:

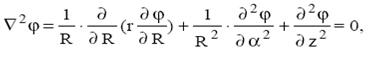[3]

где φ(R, α, z).

К уравнениям эллиптического типа относится уравнение Пуассона, которое для линейных изотропных (μх = μy = μz = μ = const) сред имеет вид:

 [5]

Где - векторный магнитный потенциал , - вектор плотности тока,

-абсолютная магнитная проницаемость среды моделирования.

Если речь идет о нелинейных средах моделирования, т.е. μ ≠ const, то из уравнений Максвелла получим

 [6]

или

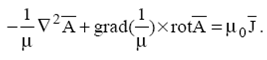 [7]

Вектор-потенциал  есть величина векторная и в декартовой системе координат

,

вектор плотности тока

.

Тогда уравнение Пуассона разбивается на три уравнения относительно скалярных величины Аx, Аy, Аz.

Если в модели ЭУ принять, что ток, а следовательно, и векторный магнитный потенциал имеют только z-составляющую, то получим плоскопараллельную или осесимметричную задачу. Для плоскопараллельного магнитного поля в декартовой системе координат можно записать уравнение Пуассона

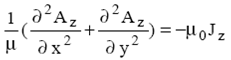 [8]

Решив данное уравнение и зная распределение векторного магнитного потенциала по области моделирования, можно найти распределение составляющих вектора магнитной индукции и результирующего значения (модуля) вектора магнитной индукции по выражениям

 [9]

Для того чтобы уравнения Лапласа-Пуассона имели единственное решение, они дополняются граничными (краевыми) условиями. На замкнутой границе Г модели ЭУ могут быть заданы следующие краевые условия.

1. Граничные условия первого рода (Дирихле) – на границе Г задается значение искомой функции, т.е. φ = f1 (x, y, z), где точки с декартовыми координатами (x, y, z) принадлежат границе Г. Условие φ = 0 является однородным.

2. Граничные условия второго рода (Неймана). Для них задается изменение искомой функции по нормали n к границе Г, т.е dφ /dn= f2 (x, y, z), где точки с координатами (x, y, z)

принадлежат границе Г. Условие dφ/dn = 0 является однородным.

3. Граничные условия третьего рода dφ /dn + f3 (φ) = f4 (x, y, z), где точки с координатами (x, y, z) принадлежат границе Г.

На границе модели могут быть заданы смешанные краевые условия, т.е. сочетание вышеприведенных – первого, второго и третьего рода.

Похожие работы

Автоматизированный анализ проектирования на микроуровне

Скачать

47503

2

14

... задачи, а именно: 1. Создана расчетная схема анализа на основании сравнительного анализа численных методов, а также программных и технических средств их осуществления; 2. Создан выбор метода автоматизированного анализа объекта проектирования; 3. Спланирован и проведен эксперимент, анализируя результаты которого, приходим к выводу, что данная модель может использоваться с параметрами: r = 5 R = ...

Стандатризация программных средств

Скачать

344008

16

23

... назначение, содержание и описание функциональных характеристик, субхарактеристик и атрибутов, определяющих специфические особенности целей, задач, свойств и сферы применения конкретного программного средства – его функциональную пригодность; ·           конструктивные характеристики качества, способствующие улучшению и совершенствованию назначения, функций и возможностей применения ПС; ...

Системы автоматизированного проектирования

Скачать

43314

0

4

... являются Лоцман:PLM компании Аскон, PDM STEP Suite, разработанная под НПО "Прикладная логистика", Party Plus компании Лоция-Софт и т.д. Итак, термин САПР (система автоматизации проектирования) подразумевает комплексный подход к разработке изделия и включает совокупность систем CAD/CAM/CAE. Развитие систем геометрического моделирования, анализа и расчета характеристик изделия сопровождается ...

Предмет и объект прикладной информатики

Скачать

308601

37

3

... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...