Навигация
Расчет силы магнитного поля на ферромагнитное основание методами программной системы конечно-элементного анализа ANSYS
3.1.3 Расчет силы магнитного поля на ферромагнитное основание методами программной системы конечно-элементного анализа ANSYS
Программная система конечно-элементного анализа ANSYS рассчитывает дискретные модели. Для вычисления силы на тело необходимо, чтобы оно было окружено хотя бы одним слоем “воздушных” элементов. Это необходимо для метода виртуальной работы при элементарном перемещении объекта на который вычисляется сила в постоянном магнитном поле. Это означает, что программа не вычисляет силу при нулевом зазоре. В качестве минимального значения зазора принят 0,1 мм.
Таблица 3.3. Зависимость силы магнитного поля, действующей на верхний магнит от воздушного зазора между магнитом и основанием.
| № | Воздушный зазор, мм. | Метод расчета силы с помощью виртуальной работы, N | Метод расчета силы с помощью тензора напряжений Максвелла |
| 1 | 0,1 | 693,88 | 693,81 |
| 2 | 0,2 | 575,27 | 575,16 |
| 3 | 0,3 | 488,55 | 488,4 |
| 4 | 0,4 | 421,83 | 421,79 |
| 5 | 0,5 | 368,85 | 368,81 |
| 6 | 0,6 | 325,76 | 325,71 |
| 7 | 0,7 | 290,07 | 290,01 |
| 8 | 0,8 | 260,07 | 260,01 |
| 9 | 0,9 | 334,57 | 234,51 |
| 10 | 1 | 212,64 | 212,58 |
| 11 | 2 | 5,31 | 95,24 |
| 12 | 3 | 51,11 | 51,04 |
| 13 | 4 | 30,1 | 30,04 |
| 14 | 5 | 18,87 | 18,81 |
3.1.4 Исследование сходимости методов расчета силы магнитного поля в зависимости от количества элементов воздушного зазора между магнитным держателем и основанием
Важно отметить, что точность вычислений силы магнитного поля на ферромагнитное основание зависит от числа элементов по длине воздушного зазора, и от самой длины воздушного зозора. В этом месте модели происходят скачки свойств материалов: постоянный магнит – воздух – ферромагнитный материал. Чтобы получить погрешность мене 1% относительно последнего результата расчетов силы по тензору Максвелла, число элементов по кратчайшему расстоянию между магнитом и объектом, на который вычисляется сила, должно быть не менее четырех, а для метода виртуальной работы достаточно двух. Это справедливо для зазора, соизмеримого с размерами магнитной системы. Для минимального зазора, рассматриваемого в данной задаче, 0.1 мм, для метода расчетов силы по тензору Максвелла с погрешностью 1% достаточно двух элементов по длине воздушного слоя, для метода виртуальной работы достаточно и 1 элемента. Эти данные справедливы только для геометрии рассматриваемой модели, и их не рекомендуется обобщать на другие расчетные модели.
Таблица 3.4 Зависимость силы магнитного поля, действующей на основание, от количества элементов по длине воздушного зазора между магнитом и основанием. Длинна воздушного зазора 5 мм.
| 5 mm | ||||
| Количество элементов по длине воздушного зазора, шт. | Метод расчета силы с помощью виртуальной работы, N | Метод расчета силы с помощью тензора напряжений Максвелла, N | Отклонение текущего значения к последнему (метод виртуальной работы) % | Отклонение текущего значения к последнему (Метод расчета с помощью тензора Максвелла) % |
| 1 | 17,967 | 11,621 | 4,765186 | 38,2256 |
| 2 | 18,846 | 17,903 | 0,106011 | 4,832022 |
| 3 | 18,842 | 18,45 | 0,127213 | 1,924304 |
| 4 | 18,849 | 18,631 | 0,090109 | 0,962152 |
| 8 | 18,866 | 18,812 | ||
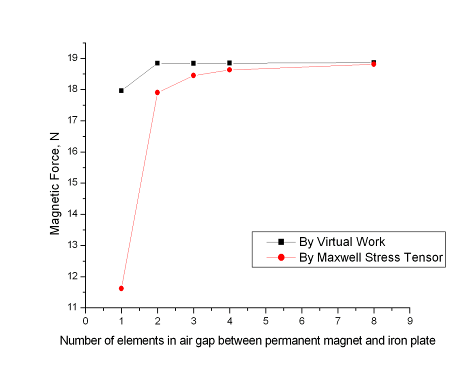
Рис. 3.8. Зависимость величины удерживающей силы от разбиения воздушного зазора, зазор 5мм.
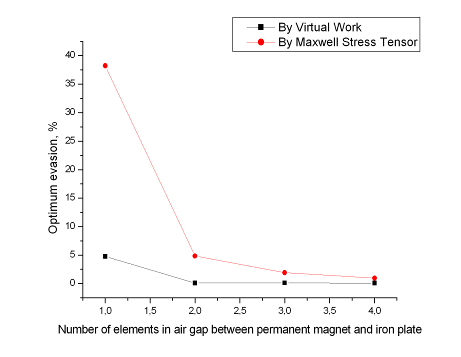
Рис.3.9 Отклонение текущей величины удерживающей силы от последней величины в зависимости от количества элементов по длине воздушного зазора, зазор 5мм.
Таблица 3.4 Зависимость силы магнитного поля, действующей на основание, от количества элементов по длине воздушного зазора между магнитом и основанием. Длина воздушного зазора 0,1 мм.
| 0,1 mm | ||||
| Количество элементов по длине воздушного зазора, шт. | Метод расчета силы с помощью виртуальной работы, N | Метод расчета силы с помощью тензора напряжений Максвелла, N | Отклонение текущего значения к последнему (метод виртуальной работы) | Отклонение текущего значения к последнему (Метод расчета с помощью тензора Максвелла) % |
| 1 | 694,37 | 692,99 | -0,0735 | 0,122507 |
| 2 | 693,95 | 693,66 | -0,01297 | 0,025943 |
| 3 | 693,9 | 693,77 | -0,00576 | 0,010089 |
| 4 | 693,88 | 693,81 | -0,00288 | 0,004324 |
| 8 | 693,86 | 693,84 | ||
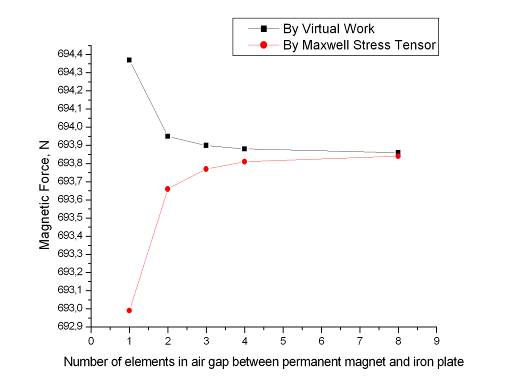
Рис. 3.10. Зависимость величины удерживающей силы от разбиения воздушного зазора, зазор 0,1мм.
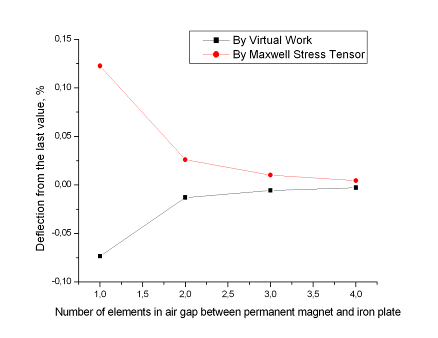
Рис.3.11 Отклонение текущей величины удерживающей силы от последней величины в зависимости от количества элементов по длине воздушного зазора, зазор 0,1 мм.
Похожие работы
... задачи, а именно: 1. Создана расчетная схема анализа на основании сравнительного анализа численных методов, а также программных и технических средств их осуществления; 2. Создан выбор метода автоматизированного анализа объекта проектирования; 3. Спланирован и проведен эксперимент, анализируя результаты которого, приходим к выводу, что данная модель может использоваться с параметрами: r = 5 R = ...
... назначение, содержание и описание функциональных характеристик, субхарактеристик и атрибутов, определяющих специфические особенности целей, задач, свойств и сферы применения конкретного программного средства – его функциональную пригодность; · конструктивные характеристики качества, способствующие улучшению и совершенствованию назначения, функций и возможностей применения ПС; ...
... являются Лоцман:PLM компании Аскон, PDM STEP Suite, разработанная под НПО "Прикладная логистика", Party Plus компании Лоция-Софт и т.д. Итак, термин САПР (система автоматизации проектирования) подразумевает комплексный подход к разработке изделия и включает совокупность систем CAD/CAM/CAE. Развитие систем геометрического моделирования, анализа и расчета характеристик изделия сопровождается ...
... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...

0 комментариев