Основные положения метода конечных элементов для решения электромагнитных задач

1.2 Основные положения метода конечных элементов для решения электромагнитных задач

В настоящее время электромагнитные задачи для электротехнических устройств со сложной геометрией как внешних, так и внутренних границ, наличием достаточного количества подобластей модели устройства с различными магнитными и проводящими свойствами решаются численными, как правило, проекционно-сеточными методами, к которым относится и метод конечных элементов как модификация проекционных методов (Ритца, Галеркина и т.д.). Суть проекционных методов состоит в попытке аппроксимировать решение дифференциального уравнения конечной линейной комбинацией базисных (пробных) функций (функций формы), т.е. в том, чтобы найти «проекцию» или приближенное решение в конечномерном пространстве для непрерывного решения в бесконечномерном функциональном пространстве. Форма базисной функции и критерий вычисления коэффициентов линейной комбинации определяют проекционный метод. [1]

Дискретная модель непрерывной области строится следующим образом.

1. В области моделирования фиксируется конечное число точек. Эти точки называются узлами расчетной сети, которой покрывается область моделирования.

2. Значение непрерывной величины в каждой узловой точке считается переменной, которая и определяется.

3. Область моделирования непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узлы, аппроксимируют форму области и представляют собой расчетную или триангуляционную сеть.

4. Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином. Они подбираются таким образом, чтобы вдоль границ элемента величина была непрерывна.

Метод конечных элементов основан на аппроксимации непрерывной функции (потенциала, температуры и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, которые называются конечными элементами. В качестве функции элемента чаще всего используется полином. Классификацию КЭ можно провести в соответствии с порядком этих полиномов. Рассматриваются три группы элементов: симплекс-, комплекс- и мультиплекс-элементы.[1]

Классическим описанием двумерного симплекс-элемента является треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине. Как правило, используется последовательная нумерация узлов против часовой стрелки, начиная от некоторого i-го узла, который выбирается произвольно. Узловые значения скалярной величины φφ обозначаются через , а координаты трех узлов – через , что позволяет определить функции формы через координаты узлов расчетной сети.

Глава II. Магнитная пружина

2.1 Численное решение

2.1.1 Постановка задачи расчета поля и силы магнитного поля исследуемой установки

Магнитная пружина представляет собой систему двух постоянных магнитов в подвижном корпусе из немагнитного материала. Корпус с одним из магнитов может перемещаться вдоль стального стержня, на верхнем конце которого зафиксирован второй магнит. Магнитная проницаемость и коэрцитивная сила постоянных магнитов равны µ=1,1, Нс=750. Магнитная проницаемость стального стержня равна µ=500.

В работе поставлены и решены следующие задачи для данного устройства с постоянными магнитами.

Расчет магнитостатического осесимметричного поля в кусочно-однородной изотропной области для различных значений воздушного зазора между постоянными магнитами. Построение эквипотенциальных линий магнитного поля.

Расчет силы магнитного поля на нижний магнит устройства методами программной системы конечно-элементного анализа ANSYS.

Исследование сходимости методов расчета силы магнитного поля в зависимости от величина воздушного пространства, окружающего магнитную систему.

Исследование сходимости методов расчета силы магнитного поля в зависимости от количества элементов модели.

Расчет силы магнитного поля на нижний магнит устройства методами программной системы конечно-элементного анализа ANSYS с использованием элементов, моделирующих затухание поля в дальней зоне (2d задача). Сравнение результатов.

Расчет магнитостатического трехмерного поля в кусочно-однородной трехмерной области. Расчет силы магнитного поля на нижний магнит устройства. Сравнение результатов.

2.1.2 Расчет магнитостатического осесимметричного поля в кусочно-однородной изотропной области для различных значений воздушного зазора между постоянными магнитами

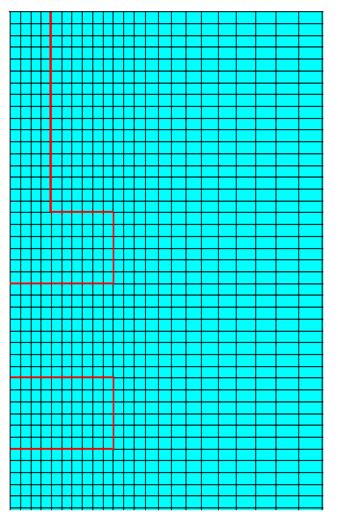
Рис 2.1. Вид созданной КЭ модели, воздушный зазор между магнитами 4мм.

В силу осесимметричности модели задача решалась в плоской постановке. Для создания КЭ модели используется элемент Plane53 – восьмиузловой элемент, для которого как геометрия, так и неизвестная функция задаются полиномом второй степени. В каждом узле он имеет одну степень свободы z-составляющую магнитного векторного потенциала Az. Тот факт, что магнитный поток принимается не выходящим за области модели, подразумевает, что поток будет параллелен внешним границам модели. Это допущение возможно, если размеры моделируемого воздушного пространства, окружающего магнитную систему, достаточны для решения поставленной задачи. Это допущение моделируется “потокопараллельным” граничным условием. Задача решалась для различных значений длины воздушного зазора между постоянными магнитами от 1-го мм до 17мм. Вид созданной КЭ модели приведен на рис.2.1 при величине воздушного зазора равного 4 мм.

Данная модель имеет 41561 узел и 13600 элементов, обладает 41561 степенью свободы.

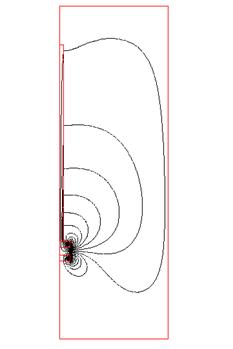
Рис.2.2 Эквипотенциальные линии магнитной индукции при величине воздушного зазора между постоянными магнитами равного 4мм.

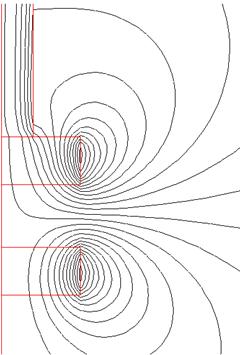
Рис 2.3 Эквипотенциальные линии магнитной индукции вблизи магнитной системы при величине воздушного зазора между постоянными магнитами равного 4мм.

Из рис. 2.2 и рис.2.3 видно, что эквипотенциальные линии магнитной индукции не выходят за внешние границы модели т.к. использовалось “потокопараллельное” граничное условие.

Похожие работы

Автоматизированный анализ проектирования на микроуровне

Скачать

47503

2

14

... задачи, а именно: 1. Создана расчетная схема анализа на основании сравнительного анализа численных методов, а также программных и технических средств их осуществления; 2. Создан выбор метода автоматизированного анализа объекта проектирования; 3. Спланирован и проведен эксперимент, анализируя результаты которого, приходим к выводу, что данная модель может использоваться с параметрами: r = 5 R = ...

Стандатризация программных средств

Скачать

344008

16

23

... назначение, содержание и описание функциональных характеристик, субхарактеристик и атрибутов, определяющих специфические особенности целей, задач, свойств и сферы применения конкретного программного средства – его функциональную пригодность; ·           конструктивные характеристики качества, способствующие улучшению и совершенствованию назначения, функций и возможностей применения ПС; ...

Системы автоматизированного проектирования

Скачать

43314

0

4

... являются Лоцман:PLM компании Аскон, PDM STEP Suite, разработанная под НПО "Прикладная логистика", Party Plus компании Лоция-Софт и т.д. Итак, термин САПР (система автоматизации проектирования) подразумевает комплексный подход к разработке изделия и включает совокупность систем CAD/CAM/CAE. Развитие систем геометрического моделирования, анализа и расчета характеристик изделия сопровождается ...

Предмет и объект прикладной информатики

Скачать

308601

37

3

... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...