Навигация
X1 + x2 + x3+2x4 + x5 =8;
12610
знаков
24
таблицы
0
изображений
4 x1 + x2 + x3+2x4 + x5 =8;
2x1 - x2 +x4=2;
x1 + x2+x5=3
L= -6x1+ x3 -x4 -x5 → max
Пусть x2, x4 – свободные переменные, а x1, x3, x5 - базисные переменные. Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
x5 =2-(1,5x2 -0,5 x4);
x3 =6-(1,5x2 +0,5 x4);
x1=1-(-0,5x2+0,5x4)
L=-2-(3x2- x4) → max
Составим симплекс-таблицу:
Выберем разрешающим столбцом x4,т.к. только перед этой переменной в целевой функции отрицательное число, выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это x1). Меняем x4 и x1
| b | x2 | x4 | ||
| L | -2 2 | 3 -1 | -1 2 | |
| x1 | 1 2 | -0,5 -1 | 0,5 2 | 1/0,5=2 |
|
| 6 -1 | 1,5 0,5 | 0,5 -1 | 6/0,5=12 |
|
| 2 1 | 1,5 -0,5 | -0,5 1 |
| b | x2 | x1 | |
| L | 0 | 2 | 2 |
| x4 | 2 | -1 | 2 |
|
| 5 | 2 | -1 |
|
| 3 | 1 | 1 |
Получили оптимальное решение, т.к. все коэффициенты положительны.
Итак, x1= x2=0, x3 =5, x4=2, x5 =3, L=0.
Ответ: x1= x2=0, x3 =5, x4=2, x5 =3, L=0.
Задача 3 (№8)
Условие:
Решение транспортной задачи:
1. Записать условия задачи в матричной форме.
2. Определить опорный план задачи.
3. Определить оптимальный план задачи.
4. Проверить решение задачи методом потенциалов.
| №вар. | а1 | а2 | а3 | b1 | b2 | b3 | b4 | b5 | с11 | с12 | с13 |
| 8 | 200 | 200 | 600 | 200 | 300 | 200 | 100 | 200 | 25 | 21 | 20 |
| с14 | с15 | с21 | с22 | с23 | с24 | с25 | с31 | с32 | с33 | с34 | с35 |
| 50 | 18 | 15 | 30 | 32 | 25 | 40 | 23 | 40 | 10 | 12 | 21 |
Решение:
Составим таблицу транспортной задачи. Заполним таблицу методом северо-западного угла:
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | 25 200 | 21 | 20 | 50 | 18 | 200 |
| A2 | 15 | 30 200 | 32 | 25 | 40 | 200 |
| A3 | 23 | 40 100 | 10 200 | 12 100 | 21 200 | 600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
Количество заполненных ячеек r=m+n-1=6.
Проверим сумму по столбцам, сумму по строкам и количество базисных (заполненных) клеток:
r =6, å ai=å bj=1000, всё выполняется, значит, найденный план является опорным.
L=25*200+30*200+40*100+10*200+12*100+21*200=22400
Постараемся улучшить план перевозок.
1) Рассмотрим цикл (1;1)-(1;2)-(2;2)-(2;1)
Подсчитаем цену цикла: j=15-30+21-25=-19<0
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | 25 | 21 200 | 20 | 50 | 18 | 200 |
| A2 | 15 200 | 30 | 32 | 25 | 40 | 200 |
| A3 | 23 | 40 100 | 10 200 | 12 100 | 21 200 | 600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
L=21*200+15*200+40*100+10*200+12*100+21*200=18600
2) Рассмотрим цикл (2;1)-(2;2)-(3;2)-(3;1)
j=-15+30+23-40=-2<0
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | 25 | 21 200 | 20 | 50 | 18 | 200 |
| A2 | 15 100 | 30 100 | 32 | 25 | 40 | 200 |
| A3 | 23 100 | 40 | 10 200 | 12 100 | 21 200 | 600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
L=21*200+15*100+30*100+23*100+10*200+12*100+21*200=18400
Проверим методом потенциалов:
Примем α1=0, тогда βj = cij – αi (для заполненных клеток).
Если решение верное, то во всех пустых клетках таблицы Δij = cij – (αi+ βj) ≥ 0
Очевидно, что Δij =0 для заполненных клеток.
В результате получим следующую таблицу:
| B1=6 | B2=21 | B3=-7 | B4=-5 | B5=4 | ai | |
| A1=0 | 25-6>0 | 21-21=0 200 | 20+7>0 | 50+5>0 | 18-4>0 | 200 |
| A2=9 | 15-9-6=0 100 | 30-21-9=0 100 | 32-9+7>0 | 25+5-9>0 | 40-4-9>0 | 200 |
| A3=17 | 23-17-6=0 100 | 40-21-17>0 | 10+7-17=0 200 | 12+5-17=0 100 | 21-4-17=0 200 | 600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
Таким образом, решение верное, т.к. Δij > 0 для всех пустых клеток и Δij =0 для всех заполненных.
Тогда сумма всех перевозок:
L=18400
Ответ:
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | 25 | 21 200 | 20 | 50 | 18 | 200 |
| A2 | 15 100 | 30 100 | 32 | 25 | 40 | 200 |
| A3 | 23 100 | 40 | 10 200 | 12 100 | 21 200 | 600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
Задача 4 (№53)
Условие:
Определить экстремум целевой функции вида
F = c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях:
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2.
1. Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
2. Составить функцию Лагранжа.
3. Получить систему неравенств в соответствии с теоремой Куна-Таккера.
4. Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
5. Дать ответ с учетом условий дополняющей нежесткости.
| № | b1 | b2 | c11 | c12 | c22 | extr | a11 | a12 | a21 | a22 | p1 | p2 | Знаки огр. 1 2 | |
| 53 | 6 | 1,5 | -2 | -4 | –1 | max | 2,5 | -1 | 3 | 2,5 | 7 | 13 | ³ | ³ |
Решение:
Целевая функция:
F= -2x12-x22-4x1x2+6x1+1,5x2→max
Ограничения g1(x) и g2(x): 2,5x1-x2³7 2,5x1-x2–7³0
3x1+2,5x2³13 3x1+2,5x2-13³0
1) определим относительный максимум функции, для этого определим стационарную точку (х10, х20):
→
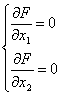2) Исследуем стационарную точку на максимум, для чего определяем выпуклость или вогнутость функции
F11 (х10, х20) = -4 < 0
F12 (х10, х20)=-4
F21 (х10, х20)=-4
F22 (х10, х20)=-2
F11 F12 -4 -4
F21 F22 -4 -2
Т.к. условие выполняется, то целевая функция является строго выпуклой в окрестности стационарной точки
3) Составляем функцию Лагранжа:
L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2x12-x22-4x1x2+6x1+1,5x2+u1 (2,5x1-x2–7)+ u2 (3x1+2,5x2-13).
Получим уравнения седловой точки, применяя теорему Куна-Таккера:
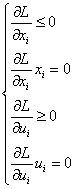i=1;2
Объединим неравенства в систему А, а равенства в систему В:
Система А:
Система В:
Перепишем систему А:
6-4x1-4x2+2,5u1+3u2 <0
1,5-4x1-2x2-u1+2,5u2 <0
2,5x1-x2–7³0
3x1+2,5x2–13³0
4)Введем новые переменные
V={v1,v2}≥0; W={w1,w2}≥0
в систему А для того, чтобы неравенства превратить в равенства:
6-4x1-4x2+2,5u1+3u2 + v1=0
1,5-4x1-2x2-u1+2,5u2 + v2=0
2,5x1-x2–7- w1=0
3x1+2,5x2–13- w2=0
Тогда
- v1=6-4x1-4x2+2,5u1+3u2
- v2=1,5-4x1-2x2-u1+2,5u2
w1=2,5x1-x2–7
w2=3x1+2,5x2–13
Следовательно, система В примет вид:
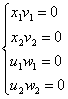- это условия дополняющей нежесткости.
5) Решим систему А с помощью метода искусственных переменных.
Введем переменные Y={y1; y2} в 1 и 2 уравнения системы
6-4x1-4x2+2,5u1+3u2 + v1 -y1=0
1,5-4x1-2x2-u1+2,5u2 + v2 -y2=0
2,5x1-x2–7- w1=0
3x1+2,5x2–13- w2=0
и создадим псевдоцелевую функцию Y=My1+My2→min
Y’=-Y= -My1-My2→max.
В качестве свободных выберем х1, х2, v1, v2, u1, u2;
а в качестве базисных y1, y2, w1, w2.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
y1=6-(4x1+4x2-2,5u1-3u2 - v1)
y2=1,5-(4x1+2x2+u1-2,5u2 -v2)
w1=-7-(-2,5x1+x2)
w2=-13-(-3x1-2,5x2)
Y’=-Y=-My1-My2=-7,5M-(-8x1-6x2+1,5u1+5,5u2+ v1+v2) M
Решим с помощью симплекс-таблицы. Найдем опорное решение:
|
|
|
|
|
|
|
| |
|
| -7,5M 4,5M | -8M 12M | -6M 3M | 1,5M 3M | 5,5M -7,5M | M 0 | M -3M |
|
| 6 -3 | 4 -8 | 4 -2 | -2,5 -2 | -3 5 | -1 0 | 0 2 |
|
| 1,5 3/4 | 4 2 | 2 0,5 | 1 0,5 | -2,5 -5/4 | 0 0 | -1 -0,5 |
|
| -7 -3/4 | -2,5 -2 | 1 -0,5 | 0 -0,5 | 0 5/4 | 0 0 | 0 0,5 |
|
| -13 15/8 | -3 5 | -2,5 5/4 | 0 5/4 | 0 -25/16 | 0 0 | 0 -5/4 |
Меняем
и 
|
|
|
|
|
|
|
| |
|
| -3M 3M | 4M -4M | 3M -2M | 4,5M -4,5M | -2M M | M -M | -2M 2M |
|
| 3 3/2 | -4 -2 | -2 -1 | -4,5 -9/4 | 2 0,5 | -1 -0,5 | 2 1 |
|
| 3/4 15/8 | 2 -2,5 | 0,5 -5/4 | 0,5 -45/16 | -5/4 5/8 | 0 -5/8 | -0,5 5/4 |
|
| -31/4 -15/8 | -4,5 2,5 | -0,5 5/4 | -0,5 45/16 | 5/4 -5/8 | 0 5/8 | 0,5 -5/4 |
|
| -89/8 75/32 | 2 -25/8 | 5/4 -25/16 | 5/4 -225/64 | -25/16 25/32 | 0 -25/32 | -5/4 25/16 |
Меняем 
и 
|
|
|
|
|
|
|
| |
|
| 0 0 | 0 0 | M 0 | 0 0 | M 0 | 0 0 | 0 0 |
|
| 3/2 77/8 | -2 -1 | -1 -3/4 | -9/4 -37/16 | 0,5 5/8 | -0,5 -5/8 | 1 3/4 |
|
| 21/8 77/32 | -0,5 -1/4 | -3/4 -3/16 | -37/16 -37/64 | 5/8 5/32 | -5/8 -5/32 | 3/4 -3/16 |
|
| -77/8 77/16 | -2 -0,5 | 3/4 -3/8 | 37/16 -37/32 | -5/8 5/16 | 5/8 -5/16 | -3/4 3/8 |
|
| -281/32 693/128 | -9/8 -9/16 | -5/16 -27/64 | -145/64 -333/256 | 25/32 45/128 | -25/32 -45/128 | 5/16 27/64 |
Меняем 
и 
|
|
|
|
|
|
|
| |
|
| 0 0 | 0 0 | M 0 | 0 0 | M 0 | 0 0 | 0 0 |
|
| 89/8 431/18 | -1 -16/9 | -7/4 | -73/16 | 9/8 | -9/8 | 7/4 |
|
| 161/32 431/72 | -1/4 -4/9 | -15/16 | -185/64 | 25/32 | -25/32 | 9/16 |
|
| 77/16 431/36 | -0,5 -8/9 | -3/8 | -37/32 | 5/16 | -5/16 | 3/8 |
|
| -431/32 431/18 | -9/16 -16/9 | -47/64 | -913/256 | 145/128 | -145/128 | 47/64 |
Меняем и 
|
|
|
|
|
|
|
| |
|
| 0 | 0 | M | 0 | M | 0 | 0 |
|
| 2525/72 | ||||||
|
| 3173/288 | ||||||
|
| 2417/144 | ||||||
|
| 431/18 |
Итак, ==
==
=
, =16,785, =11,017, =23,944, =35,07
6) Условия дополняющей нежесткости выполняются 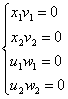,значит, решения исходной задачи квадратичного программирования существует.
Ответ: существует.
Литература.
1) Курс лекций Плотникова Н.В.
2) Пантелеев А.В., Летова Т.А. «Методы оптимизации в примерах и задачах».
Похожие работы
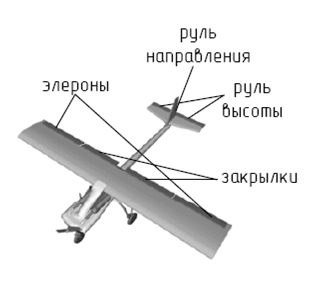
... и направление ветра, плотность воздуха и др. 4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю. Исследование операций Задача 1 Авиакомпания «Небесный грузовик», обслуживающая периферийные районы страны, располагает А1 самолетами типа 1, А2 самолетами типа 2, А3 самолетами типа 3, которые она ...
... называют системообразующие, системоохраняющие факторы, важными среди которых являются неоднородность и противоречивость ее элементов. Коммуникативность. Эта закономерность составляет основу определения системы, предложенного В. Н. Садовским и Э. Г, Юдиным в книге «Исследования по общей теории систем». Система образует особое единство со средой; как правило, любая исследуемая система представляет ...
... буржуа. М. 1987. Гвардини Р. Конец Нового времени//"Вопросы философии", 1990. Легенда о докторе Фаусте. М. 1978. I. АНТРОПОЛОГИЧЕСКАЯ ТРАДИЦИЯ В КУЛЬТУРОЛОГИИ 1. КУЛЬТУРОЛОГИЯ - ИНТЕГРАЦИЯ ЗНАНИЙ О КУЛЬТУРЕ Антропологическая традиция в культурологии — традиция исследования культуры в культурной и социальной антропологии. Культурология как интегративная наука формируется на стыке целого ряда ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
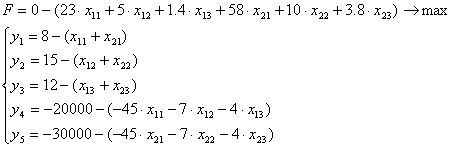
0 комментариев