Навигация
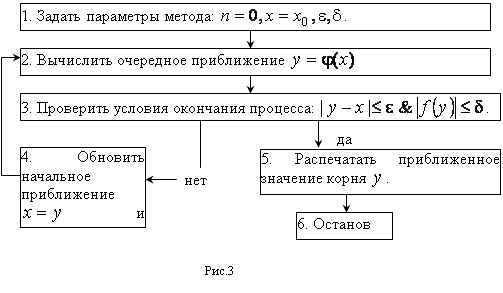
Блок-схема метода простых итераций, метода Ньютона и модифицированного метода Ньютона приведена на рисунке 3
3. Блок-схема метода простых итераций, метода Ньютона и модифицированного метода Ньютона приведена на рисунке 3.
 |
Ниже в качестве примера приведены программы на языках программирования Паскаль и С, реализующие итерационный процесс метода простых итераций.
ПРИМЕР ПРОГРАММЫ НА ЯЗЫКЕ ПАСКАЛЬ
Program Pr_iter;
Uses Crt;
var n:integer;
x0,x,eps,d,y,z,c:real;
begin
clrscr;
n:=0;x0:=-1;c:=-0.1;x:=x0;eps:=0.001;d:=0.01;
repeat
y:=x+c*(exp(x)+x);z:=x;
n:=n+1;
writeln(n:3,x:9:5,y:9:5,abs(y-x):9:5,abs(exp(y)+y):9:5);
x:=y;
until (abs(z-x)<=eps) and (abs(exp(x)+x)<=d);
end.
ПРИМЕР ПРОГРАММЫ НА ЯЗЫКЕ С
#include <stdio.h>
#include <math.h>
main()
{
int n=0;
float x,y,z,x0=-1,c=-0.1,eps=0.001;d=0.01;
x=x0;
clrscr();
do
{
y=x+c*(exp(x)+x);z=x;
printf(“%d %.4f %.4f %.4f %.4f\n”,n++,x,y,fabs(y-x),
fabs(exp(y)+y));
x=y;
}
while(fabs(z-x)>e || fabs(exp(x)+x)>d;
getch();
}
Решение: в результате решения нелинейного уравнения (1) на указанном отрезке тремя методами при начальном приближении ![]() с точностью
с точностью ![]() и
и ![]() получены следующие результаты: методом простых итераций
получены следующие результаты: методом простых итераций ![]() ; методом Ньютона
; методом Ньютона ![]() ; модифицированным методом Ньютона
; модифицированным методом Ньютона ![]() .
.
4. Содержание отчета.
Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод итерационных формул); листинг(и) программ(ы); таблицы результатов (в случае, если число итераций в таблице достаточно большое, в отчет занести две первых и две последних итерации); выводы о проделанной работе.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
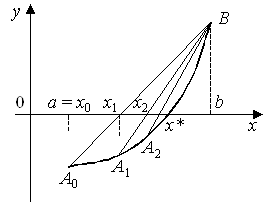
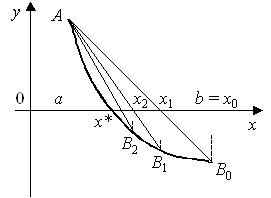
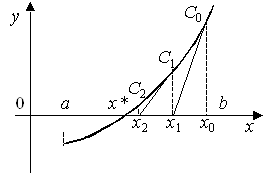
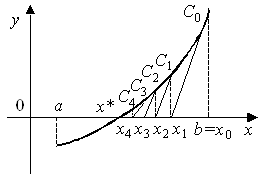
1. Определить количество корней исходного нелинейного уравнения графическим методом и построить график (пример приведен на рисунке 2).
2. Доказать аналитическим методом единственность корня исходного нелинейного уравнения на указанном отрезке.
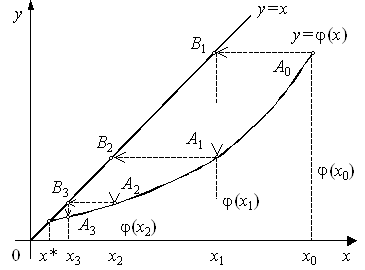
3. Построить итерационные формулы, реализующие процесс поиска корня на отрезке методом простых итераций, методом Ньютона и модифицированным методом Ньютона.
4. Составить программу(ы) на любом языке программирования, реализующую(ие) построенные итерационные процессы, используя алгоритм методов, приведенный на рисунке. Печать результатов должен осуществляться на каждом шаге итераций в виде следующей таблицы:
|
|
|
|
|
|
5. Провести вычислительные эксперименты.
6. Составить отчет о проделанной работе.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
| № варианта | Нелинейное уравнение | Отрезок |
| 1. |
|
|
| 2. |
|
|
| 3. |
|
|
| 4. |
|
|
| 5. |
|
|
| 6. |
|
|
| 7. |
|
|
| 8. |
|
|
| 9. |
|
|
| 10. |
|
|
| 11. |
|
|
| 12. |
|
|
| 13. |
|
|
| 14. |
|
|
| 15. |
|
|
| 16. |
|
|
| 17. |
|
|
| 18. |
|
|
| 19. |
|
|
| 20. |
|
|
| 21. |
|
|
Похожие работы
... - функции f. Дальше, имеем: . Отсюда , где W'(x) - транспонированная матрица Якоби. Поэтому окончательно , причем . 3. Программная реализация итерационных методов Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы: 3.1 Метод простых итераций Приведём систему к виду: Проверим условие ...
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
... искомого интервала [a, b] являются переменными величинами, которые должны задаваться в каждом конкретном случае с учетом физического смысла решаемой задачи. На втором этапе решения нелинейных уравнений полученные приближенные значения корней уточняются различными итерационными методами до некоторой заданной погрешности. Наиболее эффективные методы уточнения корней уравнения рассмотрены ниже. ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...


0 комментариев