Численные методы для решения нелинейных уравнений

Министерство общего и профессионального образования Российской Федерации

Саратовский государственный технический университет

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Методические указания

к самостоятельной работе по курсу «Высшая математика»

для студентов всех специальностей

под контролем преподавателя

Одобрено

редакционно-издательским советом

Саратовского государственного

технического университета

 

 

 

 

Саратов 2008

Введение

Данная работа ориентирована на изучение некоторых численных методов приближенного решения систем нелинейных уравнений с любым числом уравнений, составление на базе этих методов вычислительных схем алгоритмов и программ на алгоритмическом языке ФОРТРАН – IV.

Методические указания могут быть использованы как в процессе выполнения курсовой работы, так и для решения практических задач.

Задача настоящих указаний состоит в том, чтобы научить студентов решать системы нелинейных уравнений с помощью ЭВМ и затем полученные навыки использовать в курсовом и дипломном проектировании.

Предполагается, что студенты прослушали лекционный курс по основам алгоритмического языка ФОРТРАН – IV.

В качестве справочного пособия по языкам программирования может быть использована литература. [5]

Численные методы для решения нелинейных уравнений

Цель работы: изучение численных методов приближенного решения нелинейных систем уравнений, составление на базе вычислительных схем алгоритмов; программ на алгоритмическом языке ФОРТРАН – IV, приобретение практических навыков отладки и решения задач с помощью ЭВМ.

1. Определения и условные обозначения

 – конечномерное линейное пространство, элементами (точками, векторами) являются группы из  упорядоченных действительных чисел, например:

где  – действительные числа, .

В  введена операция сложения элементов, т. е.  определено отображение ,

где

Оно обладает следующими свойствами:

1.  ,

2.  ,

3.   , что  (элемент  называется нулевым),

4.  , что  (элемент  называется противоположным элементу ).

В  введена операция умножения элементов на действительные числа, т.е.  определено отображение ,

где

Оно обладает следующими свойствами:

1.  ,

2. 

Операции сложения элементов и умножения их на числа удовлетворяют законам дистрибутивности:

1.  ,

2.  .

Каждой паре элементов  поставлено в соответствие действительное число, обозначаемое символом  и называемое скалярным произведением, где

и выполнены следующие условия:

1.  ,

2.  ,

3.  ,

4.  , причем  – нулевой элемент.

Матрица  вида

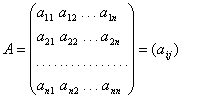
 , (1)

 

где – действительные числа (,) определяет линейный оператор, отображающий линейное пространство  в себя, а именно, для

,

где .

Над линейными операторами, действующими в линейном пространстве , вводятся следующие операции:

1.  сложение операторов , при этом, если , то ,

2.  умножение операторов на числа:  при этом, если , то ,

3.  умножение операторов: , при этом, если , то .

Обратным к оператору  называется оператор  такой, что , где  – единичный оператор, реализующий тождественное отображение, а именно,

.

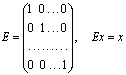Пусть число  и элемент , таковы, что .

Тогда число  называется собственным числом линейного оператора , а элемент  – собственным вектором этого оператора, соответствующим собственному числу .

Линейный оператор  называется сопряженным к оператору , если для любых элементов  выполняется равенство .

Для всякого оператора  сопряженный оператор  существует, единствен; если , то .

Справедливы равенства:

1.  ,

2.  ,

3.  ,

4.  , если  существует.

Каждому элементу  ставится в соответствие действительное положительное число, обозначаемое символом  и называемое нормой элемента .

Введем в рассмотрение три нормы для :

,

,

.

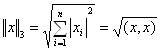При этом выполняются следующие неравенства:

.

Норма элемента удовлетворяет следующим условиям (аксиомам нормы):

1.  , причем , лишь если ,

2.  ,

3.  .

Говорят, что последовательность элементов  сходится к элементу ,

а именно, ,

или ,

если .

Определенная таким образом сходимость в конечномерном линейном пространстве  называется сходимостью по норме.

Множество элементов , удовлетворяющих неравенству  называется замкнутым (открытым) шаром в пространстве с центром в точке  и обозначается .

Каждому линейному оператору, определяемому квадратной матрицей (1), ставится в соответствие действительное неотрицательное число, обозначаемое символом  и называемое нормой линейного оператора .

Норма линейного оператора удовлетворяет следующим условиям аксиомам норм:

4.4  , причем , лишь если  – нулевая матрица,

4.4  ,

4.4  .

Введем в рассмотрение три нормы для А отображающего  в :

,

,

,

где  i-ое собственное значение матрицы .

Эти нормы линейного оператора А согласованы с соответствующими нормами элемента (вектора)  в смысле условия .

2. Основные сведения о системах нелинейных уравнений в

Общая форма систем нелинейных уравнений в  имеет вид:

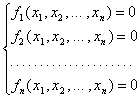(2)

или F(x) = 0,

где  – заданные функции n переменных,  – неизвестные.

Функция  при действительных значениях аргументов принимают действительные значения, т.е. являются действительнозначными. Вычислять будем только действительные решения.

Решением системы нелинейных уравнений (2) называется совокупность (группа) чисел , которые, будучи подставлены на место неизвестных , обращают каждое уравнение системы в тождество.

Частным случаем системы (2) является система линейных уравнений:

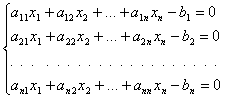
или ,

где А – матрица вида (1), порождающая линейный оператор, отображающий  в

Система линейных уравнений (2) поставим в соответствие линеаризованное уравнение (первые два члена из разложения в ряд Тейлора (2)) в точке  вида

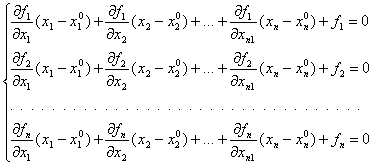(2)

или ,

где  – квадратная матрица Якоби, составленная из частных производных первого порядка функций, а именно , вычисленных точке .

Для дальнейшего нам потребуется еще одна форма записи системы нелинейных уравнений в , а именно:

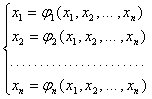(3)

или ,

где .

Операции, с помощью которых осуществляется преобразование системы (2) к системе (3), могут быть любыми, необходимо только, чтобы искомое решение системы (3) удовлетворяло системе (2).

Функции  удовлетворяют тем же условиям, что и функции .