Імовірнісні методи ощадливого кодування інформації

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

Кафедра: “Обчислювальна техніка та програмування”

Реферат

Імовірнісні методи ощадливого кодування інформації

Харків 2009

Зміст

Вступ

1. Імовірнисний підхід у теорії ощадливого кодування

1.1      Оцінка інформативності ознак

1.2 Оптимальна градація ознак

1.3 Градація перших 100 чисел натурального ряду

1.4 Градація яркостей зображеннь

2. Застосування імовірнісних методів для підвищення ефективності ощадливого кодування відеоінформації

2.1 Загальна теорія

2.2 Методи із пророкуванням

2.3 Методи прогресивного кодування

2.4 Квантування

3. Ефективні алгоритми кодування інформації

3.1 Алгоритм медіанного перетину

3.2.1 Методи кластерізації для квантування зображення

3.2.2 Метод К-середніх

3.2.3 Метод связности графа

3.2.4 Іерархічний метод

3.2.5 Метод динамічних згущеннь

4. Висновок

Список джерел

Вступ

На сьогоднішній день актуальна проблема зберігання й передачі інформації в цифровому виді. Для одержання компактних інформаційних подань застосовуються технології ощадливого кодування. Використання цих технологій дозволяє істотно знизити вимоги, пропоновані до обсягу інформаційних носіїв, а також відчутно збільшує швидкість передачі інформації з каналів зв'язку.

Передача інформації є основною областю застосування ощадливого кодування. На даний момент першочергове завдання - організація ефективного телевізійного й мультимедийного віщання. Як відомо, відеоінформація являє собою найбільш об'ємний тип інформації. З обліком обмеженої пропускної здатності цифрових каналів, щоб гарантувати високу якість передачі зображень, необхідно забезпечити їх досить ефективне подання (якість передачі прямо залежить від обсягу інформації, переданого в одиницю часу). Як наслідок, протягом уже більше 15 років значні зусилля направляються на розробку технологій ефективного подання зображень. Цій проблемі присвячена й дана дипломна робота.

Основна мета роботи - аналіз існуючих технологій одержання компактних подань відеоінформації з погляду способу організації кодування й пошук можливих шляхів підвищення їхньої ефективності.

Вибір напрямку дослідження заснований на результатах порівняльного аналізу існуючих алгоритмів ощадливого кодування. Алгоритм ощадливого кодування являє собою певний спосіб генерації ощадливого коду на основі наближеної моделі породження кодуємой інформації. З метою зниження обчислювальної складності на практиці довгий час застосовувалися спрощені методи інформаційного моделювання й генерації коду. Як моделі бралися найпростіші комбінаторні моделі, а генерація коду здійснювалася з використанням найбільш швидких реалізацій префиксного кодування. У цей час постановка завдання змінилося: на перший план стала всі частіше виходити ефективність кодування. Сьогодні стає доцільним застосування більше складних технологій кодування, які дозволяють досягти максимально компактного інформаційного подання.

Одним з найбільш ефективних методів інформаційного моделювання є імовірнісне контекстно-залежне моделювання. При використанні даного методу вибір інформаційної моделі в кожен момент часу здійснюється на основі значення деякого контексту, що формується з елементів уже обробленої інформаційної вибірки. Уводячи контексти, ми фактично вирішуємо завдання ідентифікації станів інформаційного джерела. Для кожної моделі зберігається статистична інформація про появу різних символів інформаційного алфавіту в контексті, що відповідає даної моделі. На основі цієї інформації формується розподіл імовірнісних оцінок появи символів на виході джерела, що є основою для генерації коду.

Арифметичне кодування являє собою найбільш ефективний метод генерації коду по заданому імовірнісному розподілі. Використання цього методу дозволяє одержувати коди, довжини яких мало відрізняються від теоретично оптимальних значень.

Таким чином, сполучення контекстно-залежного імовірнісного моделювання й арифметичного кодування найбільше вигідно з погляду ефективності.

1.         Імовірнісний підхід у теорії ощадливого кодування

Теорія ощадливого кодування займається проблемою створення ефективних подань інформаційної вибірки. Мова в більшості випадків іде про вибірку джерел дискретної інформації з кінцевим алфавітом. Ефективне кодування стає можливим завдяки наявності в інформації певних особливостей, тому однієї з найбільш важливих завдань є одержання як можна більше точного опису властивостей інформаційних джерел.

Існує кілька підходів до такого роду опису. Найбільше часто використовувані - комбінаторний й імовірнісний.

У рамках комбінаторного підходу символи розглядаються не обособленно, а групами, іменованими інформаційними повідомленнями. Покладається, що з виходу джерела інформації можуть надходити не всі можливі повідомлення, а тільки повідомлення з деякого виділеної безлічі. При цьому повідомлення, що належать даній безлічі, уважаються зовсім рівнозначними, тобто їхня поява покладається равновероятным. Конкретний вибір безлічі припустимих повідомлень виконує роль інформаційного опису.

Комбінаторний підхід одержав досить широке поширення на практиці. Основним його достоїнством є простота опису інформаційних особливостей, тому практичні реалізації методів ощадливого кодування, в основі яких лежить даний підхід, мають низьку обчислювальну складність.

Недолік полягає в тім, що точність опису часом прямо залежить потужності безлічі припустимих повідомлень - для одержання досить точного опису може знадобитися розглянути дуже велика кількість повідомлень. Комбінаторний підхід також не дозволяє одержувати інформаційні характеристики для окремих символів усередині повідомлення.

Суть імовірнісного підходу полягає у використанні імовірнісних оцінок фактів появи різних символів на виході джерела інформації. У порівнянні з комбінаторним підходом імовірнісний підхід є більше точним способом опису властивостей інформаційних джерел. У той же час імовірнісний підхід менш вигідний з обчислювальної точки зору, тому що його застосування сполучене з обчисленням складних імовірнісних оцінок. Таким чином, з одного боку, імовірнісний опис, як правило, більш ефективно в порівнянні з комбінаторним описом, з іншого боку, імовірнісний опис не завжди можна використати на практиці через існуючі обчислювальні обмеження. Постійне збільшення продуктивності обчислювальних систем робить останній фактор менш значимим, внаслідок чого імовірнісний підхід останнім часом все частіше й частіше береться за основу при розробці алгоритмів ощадливого кодування.

Обробка багатомірних даних, що описують досліджувані процеси й об'єкти, припускає виконання над ними деякого перетворення з метою одержання інформації про об'єкти дослідження. Така інформація звичайно втримується в структурних особливостях оброблюваних даних. Можливості методу показані на рішенні двох актуальних завдань - оцінки інформативності ознак розпізнавання й градації числових масивів. Продемонструємо саму ідею одержання інформації про структуру даних й її практичного використання. На нашу думку пропонований метод буде сприяти розвитку інформаційного підходу до обробки даних.

У цей час є чудові керівництва, у яких відбитий сучасний рівень використання інформаційних мір в аналізі й обробці даних. Успіх цих підходів базується на використанні імовірнісної міри, що дозволяє апріорну інформацію представляти у вигляді законів розподілу відповідних випадкових величин, формувати критерії якості обробки даних. Однак далеко не завжди виконуються умови реалізації теоретико-імовірнісних методів. Обмеження добре відомі й це, насамперед, недостатність обсягу вихідних даних в аналізованих вибірках, невизначеність умов їхнього одержання, вплив різного роду перешкод і т.п. Альтернативою традиційним підходам може служити підхід, у якому завдання одержання інформаційного критерію якості вирішується в екстремальній постановці. При такому підході можлива розробка адаптивних алгоритмів, що володіють більшою стійкістю до впливу перешкод і не потребуючих для одержання статистично стійкого результату більших обсягів вхідних даних. Однак рішення оптимизационных завдань при обробці багатомірних даних, як правило, вимагає більших обчислювальних ресурсів. Тому необхідно пошук класу цільових функцій, що допускає прості алгоритми обчислення экстремумов. До таких функцій можна віднести не тільки лінійні й квадратичні функції, але й позиномы. Для них розроблені ефективні методи рішення оптимизационных завдань, відомі як завдання геометричного програмування. Більше того, що з'явилися останнім часом аналітичні методи їхні рішення дозволяють сподіватися на успіх застосування позиномов в аналізі даних.

Одночасно при обробці багатомірних даних у гнітючому числі випадків вирішується завдання їхнього агрегування. Як такі агрегати звичайно використаються середні величини й, зокрема, середні статечні. Серед останніх особливими властивостями володіють середнє арифметичне й середнє гармонійне. Їхнє відношення має властивості ентропії, значення якої можна інтерпретувати як міру невизначеності у виборі елементів масиву. Однак тут нас буде цікавити інший аспект зазначеного відношення, а саме - відношення як міра структурних розходжень значень компонент одномірного масиву. Оскільки розходження лежать в основі поняття інформації, те природної є спроба використання цієї міри для побудови інформаційного критерію. Для формального викладу зробимо необхідні позначення.

Нехай  матриця з позитивними елементами , що має  рядків і  стовпців і нехай . Для кожної матриці  можна визначити функцію

, (1)

де  - транспонована матриця, елементи якої є зворотними значеннями елементів матриці .

При фіксованих значеннях елементів матриці  функція (1) буде залежати від компонентів вектора . Бажаючи підкреслити цей факт, будемо для  використати також позначення . Можна показати, що  має основні властивості ентропії. Якщо рядка матриці  різні за структурою значень своїх елементів, то максимальне значення (1) досягається на векторі , відмінному від рівномірного 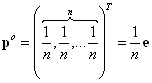. Компоненти вектора  мають цікаву властивість: дві максимальні за своїми значеннями компонента відповідають двом об'єктам (рядкам матриці ), які найбільшою мірою відрізняються друг від друга структурою значень своїх елементів (найбільш деструктивні). Це властивість вектора  можна використати при розробці алгоритмів класифікації.

Возможность використання властивостей вектора  для рішення завдання кластеризации даних квітів ірису на три класи - virginic, versicol й setosa з покажемо на прикладі. На мал. 1 показаний графік значень компонент вектора  для всієї вибірки. Як видно найбільші значення компонентів вектора відповідають двом елементам: [7,2 3,6 6,1 2,5]; [4,3 3,0 1,1 0,1].

На першому кроці з використанням міри близькості

 

виявилося можливим розбити всю сукупність характеристик квітів ірису на два кластери по ступені їхньої близькості до виділених елементів по алгоритму. Отримані в результаті кластери, перший - квіти virginic й versicol, другий - квіти setosa. На другому кроці після проведення аналогічної процедури для даних першого кластера спостерігалися 9 помилок, які розподілилися між класами (квітами) як 5 до 4.

  

Рис.1 Графік зміни компонент вектора  для всієї вибірки характеристик квітів ірису.

Загальні результати класифікації, представлені у вигляді матриці переплутування

.

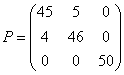Їх можна віднести до одним із кращих результатів кластеризации квітів ірису, що демонструє можливість використання інформаційних властивостей вектора  для побудови алгоритмів класифікації багатомірних даних. Можна продовжити дослідження в цьому напрямку для різних вирішальних правил у процедурах класифікації, однак, залишаючи осторонь деталі, підкреслимо, що запропонований спосіб виявлення розходжень є основою для розробки ефективних алгоритмів розпізнавання.

Повернемося до основної мети нашого дослідження з формування інформаційного критерію. Розглянемо окремий випадок, коли матриця  складається з одного вектора-стовпця . Для цього випадку представимо формулу у вигляді

.

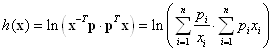Легко перевірити, що

1. ;

2.  

3. .

На підставі цих властивостей будемо функцію (4) називати мірою розходжень компонент вектора  або інформаційною мірою, оскільки, там, де є розходження, там є й інформація. Далі, визначимо

 

і шуканий інформаційний критерій

,

де ( ) і ( ) -заелементні операції розподілу й множення відповідно.

Область  визначається умовами розв'язуваного завдання. Приведемо приклади використання формули (7). Почнемо із простого випадку. Нехай перетворення полягає в заміні вихідного вектора  вектором . Тоді область обмежень  визначиться співвідношеннями , а величина - рівністю

,

звідки треба, що максимально можлива кількість інформації втримується в тотожному перетворенні й дорівнює

,

що й випливало очікувати.

Розглянемо більше складні й практично важливі приклади.