Навигация
2. Квадратурні формули.
2.1. Формула прямокутників.
Припустимо, що fÎC2[-h/2,h/2], h>0 .
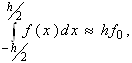 (2.1.1)
(2.1.1)
де f0=f(0), тобто площа криволінійної трапеції, обмеженої зверху графіком функції f(x) , апроксимується площею прямокутника, висота якого дорівнює значенню f(x) в середній точці трапеції (мал. 2.1.1).
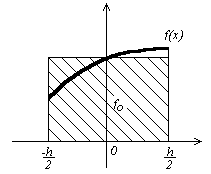
мал. 2.1.1. Формула прямокутників
Знайдемо залишковий член , тобто похибку формули (2.1.1) . Нехай
![]() (2.1.2)
(2.1.2)
![]() Тому що F(0)=0, F/(0)=f0, F//(0)=f/0, F///(x)=f//0,
Тому що F(0)=0, F/(0)=f0, F//(0)=f/0, F///(x)=f//0,
то відповідно до формули Тейлора з залишковим членом у формі Лагранжа маємо
![]()
![]() (2.1.3)
(2.1.3)
де x- , x+ - деякі точки , -h/x-<x+<h/2.
Функція F(x) є первісної для f(x). Тому для інтеграла, що стоїть в лівій частині наближеної рівності (2.1.1), з формули Ньютона-Лейбница з розрахунком (2.1.3) випливає наступне співвідношення
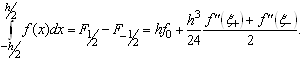
Ззвідси одержуємо формулу прямокутників із залишковим членом:
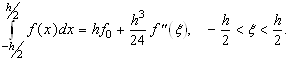 (2.1.4)
(2.1.4)
2.2. Формула трапецій.
Нехай fÎC2[0,h], h>0
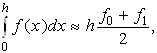 (2.2.1)
(2.2.1)
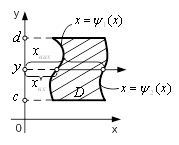
де f0=f(0), f1=f(h) тобто інтеграл 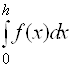 приблизно заміняється площею заштрихованої трапеції, показаної на малюнку (мал. 2.2.1).
приблизно заміняється площею заштрихованої трапеції, показаної на малюнку (мал. 2.2.1).
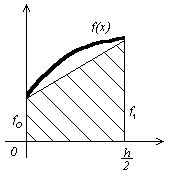
мал. 2.2.1. Формула трапецій.
Знайдемо залишковий член, тобто похибку формули (2.2.1). Виразимо f1та F1=F(h) де F - функція (2.1.2), по формулі Тейлора з залишковим членом в інтегральній формі (*):
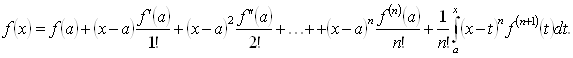 (*)
(*)
![]() (2.2.2)
(2.2.2)
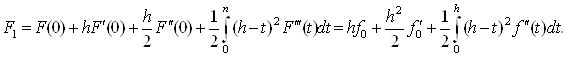 (2.2.3)
(2.2.3)
Згідно (2.2.1) маємо
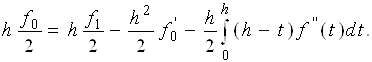 (2.2.4)
(2.2.4)
Відокремивши в правій частині (2.2.3) доданок hf0/2 і замінивши його вираженням (2.2.4), з урахуванням того, що
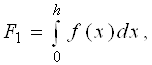
знаходимо
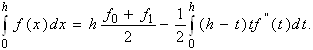
Перетворимо тепер другий доданок у правій частині, використовуючи узагальнену теорему про середнє. Тому що (h-t)t³0, tÎ[0,t] то за теоремою
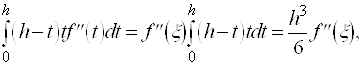
де xÎ[a,b] - деяка точка . Підставляючи отримане в (*), приходимо до формули трапецій із залишковим членом :
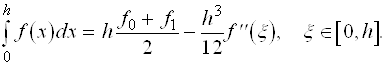 (2.2.5)
(2.2.5)
2.3. Формула Сімпсона .
Припустимо, що fÎC4[-h,h]. Тоді інтеграл
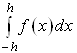
наближеного заміняємо площею заштрихованої криволінійної трапеції, обмеженою зверху параболою, що проходить через точки (-h,f-1), (0,f0), (h,f1), де fi=f(ih) (мал. 2.3.1)
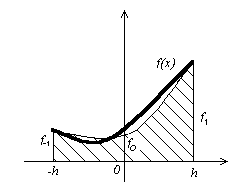
мал. 2.3.1 Формула парабол (Сімпсона)
Зазначена парабола задається рівнянням
![]()
у цьому неважко переконатися, поклавши x=-h, x=0, x=h (її можна також одержати, побудувавши інтерполяційний багаточлен другого ступеня і приводячи подібні ). Звідси знаходь
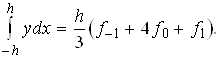
Таким чином, формула Сімпсона , називають також формулою парабол, має вид
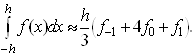 (2.3.1)
(2.3.1)
Покладемо F±1=F(±h), де F функція (2.1.2). Оскільки F(0)=0, F(k)(x)=
f(k-1)(x), 1£k£5 то згідно формули Тейлора з залишковим членом в інтегральній формі маємо

Звідси одержуємо
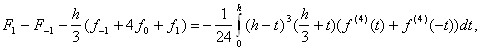 (2.3.2)
(2.3.2)
тому що інші члени взаємно знищуються.
Оскільки ![]() , tÎ[0,h] то застосовуючи до інтеграла (2.3.2) узагальнену теорему про середнє, знаходимо
, tÎ[0,h] то застосовуючи до інтеграла (2.3.2) узагальнену теорему про середнє, знаходимо
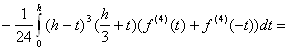
![]() (2.3.3)
(2.3.3)
де hÎ[0,h], xÎ[-h,h] - деякі точки. Приймаючи до уваги, що
![]()
з (2.3.2), (2.3.3) приходимо до формули
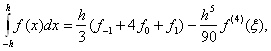 (2.3.4)
(2.3.4)
тобто до формули Сімпсона з залишковим членом.
Похожие работы
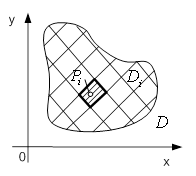
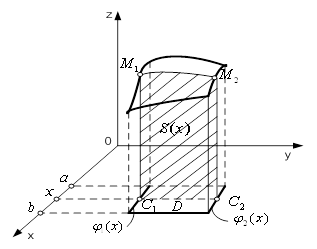
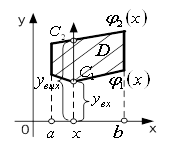
... йного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів. Покажемо, як це робиться. Припустимо, що при функція . Тоді, згідно з формулою (7), подвійний інтеграл виражає об'єм циліндричного тіла (рис.3) з основою , обмеженого зверху поверхнею . Обчислимо цей об'єм за допомогою методу паралельних перерізів [6]: , де - площа перерізу тіла ...
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...
... Методичні вказівки до лабораторної роботи № З «Тепловіддача горизонтальної труби при вільному русі повітря». Тернопіль 2003 У даних методичних вказівках подані теоретичні основи, опис експернментальної установки і практичні рекомендації лля проведення лабораторної роботи і обробки дослідних даних Мета роботи - засвоїти знання з теорії" конвсктивнот теплообміну при ...
р, формула Гріна, функція Рімана. Мета роботи: в даній роботі необхідно ознайомитись з методом отримання розв’язку задачі Гурса для телеграфного рівняння (1.1) з початковими умовами (1.2); довести існування та єдиність цього розв’язку; навести приклади та вказати області вживання цього методу у прикладних науках. The summary. In the given operation some questions, concerning ...


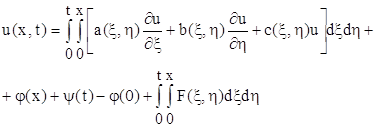
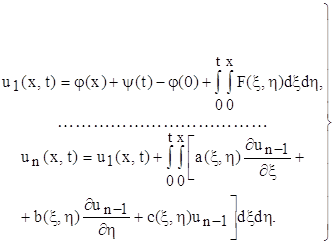
0 комментариев