Навигация
Чисельні методи знаходження визначеного
3. Чисельні методи знаходження визначеного
Інтеграла зі змінною верхньою межею
У деяких випадках необхідно обчислити такі інтеграли
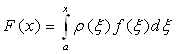
Можна, звичайно, розглядати його для кожного значення верхньої границі х як інтеграл зі сталими границями і обчислювати за однією з квадратурних формул, що невигідно у випадку великої кількості значень x. Краще вибрати деяку сітку і скласти таблицю значень інтеграла на цій сітці Fn=F(x) за квадратурної формули високої точності. Тоді
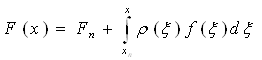
![]() (3.1)
(3.1)
причому останній інтеграл можна одчислювати за простими квадратурними формулами.
Окрім того, маючи таблицю F(xn), можна знаходити F(x) інтерполяцією за цією таблицею. Природно, маючи і похідну інтеграла F¢(x)=r(x)f(x). Краще скористатись інтерполяційним поліномом Ерміта.
4. Опис обчислювального алгоритму
При реалізаціі алгоритму обчислення визначеного інтеграла зі змінними границями інтегрування використовуються процедури та функцiї, для того щоб скоротити витрати машинного часу при обчислюваннi, та для компактностi программи. Программа для знаходження написана на мовi Delphi5, стан пограмми – вiдлажена.
5. Обговорювання результатів
Таблиця 1
| Формула (3.1) | Формула Сімпсона | Формула трапецій | Дійсне значення інтеграла | |
| a=0; b=1; | -0.7974398040 Різниця 0.0000012883 | -0.7974386790 Різниця 0.0000001633 | -0.7993252434 Різниця 0.00188672780 | -0.7974385156 |
| a=0; b=2; | 3.9190337956 Різниця 0.0000062805 | 3.9190353338 Різниця 0.0000047422 | 3.90875628130 Різниця 0.01028379486 | 3.9190400761 |
| a=0; b=3; | 10.5498688094 Різниця 0.00002744251 | 10.5498688094 Різниця 0.00002744251 | 10.5247085565 Різниця 0.02518769537 | 10.5498962519 |
| a=0; b=4; | 17.8842287345 Різниця 0.0000804723 | 17.8842201707 Різниця 0.00008903613 | 17.8382724576 Різниця 0.0460367491 | 17.8843092068 |
| a=0; b=5; | 25.5043003647 Різниця 0.0001835185 | 25.5042688642 Різниця 0.00021501907 | 25.4318420115 Різниця 0.0726418717 | 25.5044838833 |
| a=0; b=6; | 33.2576007639 Різниця 0.00035637138 | 33.2575244054 Різниця 0.00043272988 | 33.1529684530 Різниця 0.1049886822 | 33.2579571352 |
Таблиця 1 була отримана при наступних вхідних даних:
Кількість вузлів при побудові таблиці значень інтегралу (1) =20
Кількість вузлів при застосуванні формули трапецій =20
Кількість вузлів при застосуванні формули Сімпсона =20
ВисновкиТаким чином з таблиці 1 видно, що чим більший проміжок ми беремо тим кращу точність отримаємо, навіть краще за формулу Сімпсона, але загальна похибка (відносно дійсного значення) також збільшується. Формулу (1) доцільно використовувати, якщо потрібно обчислити інтеграл на відносно великому проміжку та якщо треба обчислити відразу декілька інтегралів.
Список посилань
1. Каліткін Н.Н. ‘Чисельні методи’ – М.: Наука, 1978. – 512 с.
2. Балашова С.Д. ‘Тексты лекций по курсу “ Численные методы”’. – Днепропетровск: Из – во ДГУ, 1989. – 206 с
3. Мусiяка В.Г. Основи чисельних методiв механiки. – Днiпропетровськ: Вид – во ДДУ, 1993. – 156 с.
4. Методические рекомендации по курсу “ Методы вычислений в инженерных расчётах”/ Составитель В.Г. Мусияка. – Днепропетровск: Из – во ДГУ, 1992. – 40 с.
5. Фіхтегольц Г.М. ‘Основи математичного аналізу’– М.: Наука, 1968. – 440 с.
Д О Д А Т К И
А Опис вихiдних даних та результатiв розрахунку
Вихiднi данi
Кількість вузлів при побудові таблиці значень інтегралу (1) nGrid - integer;
Кількість вузлів при застосуванні формули трапецій nTrap - integer;
Кількість вузлів при застосуванні формули Сімпсона nSim - integer;
Границі інтегрування a і b – real;
Наслiдки виконання програми друкуються у виглядi:

Вихідні дані це функції типа real.
FullIntegral(L,R);
integralSimpsona(L,R);
integralTrapeciay(L,R);
first(L,R);
B Схемаобчислювального алгоритму
Функція y(x) тип real Функція first(x1,x2) тип real
 | |||
 | |||
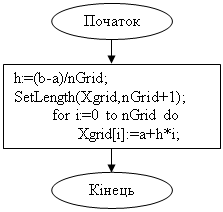
Процедура createGrid Процедура createGridOfInt
 | |||
 | |||
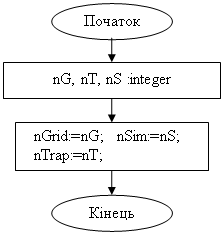
Процедура setN(nG, nT, nS )
Функція integralSimpsona(aSim,bSim) тип real
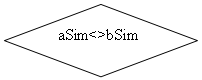
![]()
![]()
![]()
|
так ні

Функція integralTrapeciay(aTrap,bTrap) тип real
 | |||
Функція FullIntegral(aFull,bFull:real) тип real
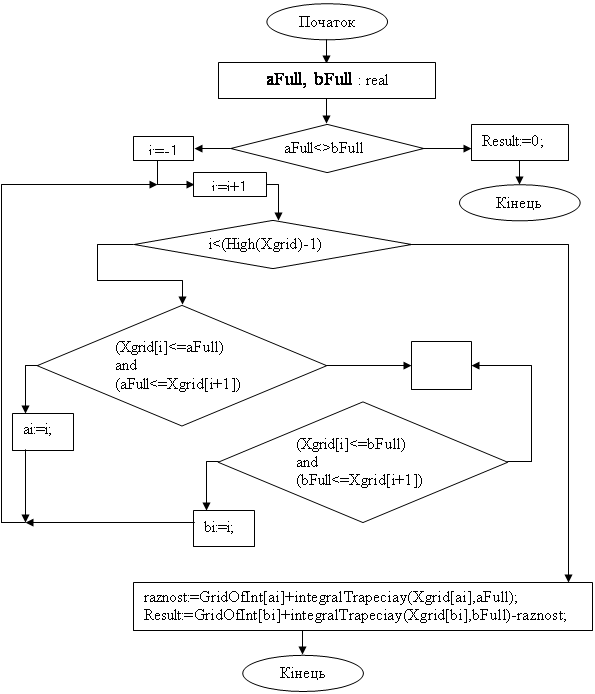
так ні
так ні

так ні
так ні
С Лiстiнг програми
unit funct;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, ExtCtrls, Math;
const
a = 0;
b = 6;
type
one_array = array of real;
Parametrs = record
nSimp, nTrap :integer;
end;
function y(x:real):real;
function first(x1,x2:real):real;
procedure setN(nG, nT, nS :integer);
procedure createGrid;
procedure createGridOfInt;
function integralSimpsona(aSim,bSim:real):real;
function integralTrapeciay(aTrap,bTrap:real):real;
function FullIntegral(aFull,bFull:real):real;
var
Xgrid:one_array; GridOfInt:one_array; nGrid, nSim, nTrap :integer;
implementation
//--------------------------------------------------------------
function y(x:real):real;
begin
Result:=2*arctan(x)-11*Power(3,(-x))+5;
end;
//--------------------------------------------------------------
function first(x1,x2:real):real;
begin
result:=5*x2+2*x2*ArcTan(x2)+11*Power(3,(-x2))/Ln(3)-Ln(1+x2*x2)-(5*x1+2*x1*ArcTan(x1)+11*Power(3,(-x1))/Ln(3)-Ln(1+x1*x1));
end;
//--------------------------------------------------------------
procedure setN(nG, nT, nS :integer);
begin
nGrid:=nG; nSim:=nS; nTrap:=nT;
end;
//--------------------------------------------------------------
procedure createGrid;
var i:integer; h:real;
begin
h:=(b-a)/nGrid;
SetLength(Xgrid,nGrid+1);
for i:=0 to nGrid do
Xgrid[i]:=a+h*i;
end;
//--------------------------------------------------------------
procedure createGridOfInt;
var i, n :integer;
begin
n:=High(Xgrid);
SetLength(GridOfInt,n+1);
for i:=1 to n do
GridOfInt[i]:=integralSimpsona(a,Xgrid[i]);
end;
//--------------------------------------------------------------
function integralSimpsona(aSim,bSim:real):real;
var X:one_array; i:integer; sum1, sum2, h:real;
begin
if(aSim<>bSim)then
begin
h:=(bSim-aSim)/nSim;
SetLength(X,nSim+1);
for i:=0 to nSim do
X[i]:=aSim+h*i;
sum1:=0;
sum2:=0;
for i:=1 to (nSim div 2) do
sum1:=sum1+y(X[2*i-1]);
for i:=1 to ((nSim div 2)-1) do
sum2:=sum2+y(X[2*i]);
Result:=(bSim-aSim)*(y(X[0])+y(X[nSim])+4*sum1+2*sum2)/(3*nSim);
end
else
Result:=0;
end;
//--------------------------------------------------------------
function integralTrapeciay(aTrap,bTrap:real):real;
var i:integer; sum, h :real; X:one_array;
begin
h:=(bTrap-aTrap)/nTrap;
SetLength(X,nTrap+1);
for i:=0 to nTrap do
X[i]:=aTrap+h*i;
sum:=(y(X[0])+y(X[nTrap]))/2;
for i:=1 to (nTrap-1) do
sum:=sum+y(X[i]);
Result:=sum*h;
end;
//--------------------------------------------------------------
function FullIntegral(aFull,bFull:real):real;
var z1, z2, z3, raznost :real; i, ai, bi :integer;
begin
if(aFull<>bFull)then
begin
for i:=0 to (High(Xgrid)-1) do
begin
if((Xgrid[i]<=aFull)and(aFull<=Xgrid[i+1]))then ai:=i;
if((Xgrid[i]<=bFull)and(bFull<=Xgrid[i+1]))then bi:=i;
end;
raznost:=GridOfInt[ai]+integralTrapeciay(Xgrid[ai],aFull);
Result:=GridOfInt[bi]+integralTrapeciay(Xgrid[bi],bFull)-raznost;
end
else
Result:=0;
end;
//--------------------------------------------------------------
end.
unit UnitMAIN;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs, jpeg, ExtCtrls, StdCtrls, funct;
type
TForm1 = class(TForm)
Image1: TImage; Image2: TImage; Button1: TButton; Image3: TImage; Edit1: TEdit; Edit2: TEdit;
Label1: TLabel; Label2: TLabel; Label3: TLabel; Memo1: TMemo; Panel1: TPanel; Button2: TButton;
Button3: TButton; Label4: TLabel; Label5: TLabel; Label6: TLabel; Label7: TLabel; Edit3: TEdit;
Edit4: TEdit; Edit5: TEdit; Label8: TLabel;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
end;
var
Form1: TForm1;
implementation
{$R *.DFM}
procedure TForm1.Button1Click(Sender: TObject);
var i:integer; intF, intS, intT, intR, L,R:real; file1:TextFile;
begin
L:=StrToFloat(Edit1.Text); R:=StrToFloat(Edit2.Text);
if(((0<=L)and(L<=6))and(((0<=R)and(R<=6))))
then
begin
createGrid;
createGridOfInt;
intF:=FullIntegral(L,R);
Label1.Caption:=FloatToStr(intF);
intS:=integralSimpsona(L,R);
intT:=integralTrapeciay(L,R);
intR:=first(L,R);
AssignFile(file1,'Result.txt');
Rewrite(file1);
writeln(file1,'Дйствительное значение интеграла ',intR:17:15);
writeln(file1,'Значение интеграла по формуле (1) ',intF:17:15,' Расность по модулю ',abs(intF-intR):17:15);
writeln(file1,'Значение интеграла по формуле трапеций ',intT:17:15,' Расность по модулю ',abs(intT-intR):17:15);
writeln(file1,'Значение интеграла по формуле Симпсона ',intS:17:15,' Расность по модулю ',abs(intS-intR):17:15);
CloseFile(file1);
Memo1.Lines.LoadFromFile('Result.txt');
end
else ShowMessage('граници должна быть в пределах от 0 до 6');
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
Panel1.Visible:=true; Button2.Visible:=false;
end;
procedure TForm1.Button3Click(Sender: TObject);
begin
Panel1.Visible:=false; Button2.Visible:=true;
setN(StrToInt(Edit5.Text),StrToInt(Edit3.Text),StrToInt(Edit4.Text));
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
setN(StrToInt(Edit5.Text),StrToInt(Edit3.Text),StrToInt(Edit4.Text));
end;
end.
Похожие работы
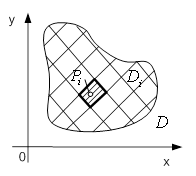
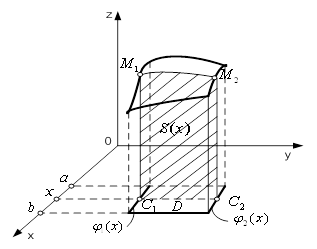
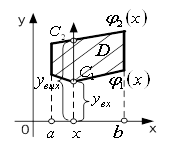
... йного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів. Покажемо, як це робиться. Припустимо, що при функція . Тоді, згідно з формулою (7), подвійний інтеграл виражає об'єм циліндричного тіла (рис.3) з основою , обмеженого зверху поверхнею . Обчислимо цей об'єм за допомогою методу паралельних перерізів [6]: , де - площа перерізу тіла ...
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...
... Методичні вказівки до лабораторної роботи № З «Тепловіддача горизонтальної труби при вільному русі повітря». Тернопіль 2003 У даних методичних вказівках подані теоретичні основи, опис експернментальної установки і практичні рекомендації лля проведення лабораторної роботи і обробки дослідних даних Мета роботи - засвоїти знання з теорії" конвсктивнот теплообміну при ...
р, формула Гріна, функція Рімана. Мета роботи: в даній роботі необхідно ознайомитись з методом отримання розв’язку задачі Гурса для телеграфного рівняння (1.1) з початковими умовами (1.2); довести існування та єдиність цього розв’язку; навести приклади та вказати області вживання цього методу у прикладних науках. The summary. In the given operation some questions, concerning ...


0 комментариев