Навигация
Теоретическая часть
2. Теоретическая часть
Математические модели
Математическая модель — приближенное описание объекта моделирования, выраженное с помощью математической символики.
Математические модели появились вместе с математикой много веков назад. Огромный толчок развитию математического моделирования придало появление ЭВМ. Применение вычислительных машин позволило проанализировать и применить на практике многие математические модели, которые раньше не поддавались аналитическому исследованию. Реализованная на компьютере математическая модель называется компьютерной математической моделью, а проведение целенаправленных расчетов с помощью компьютерной модели называется вычислительным экспериментом.
Этапы компьютерного математического моделирования изображены на рисунке (1). Первый этап —определение целей моделирования. Эти цели могут быть различными:
1. модель нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание);
2. модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);
3. модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).
4. Построение математической модели. На этом этапе происходит переход от абстрактной формулировки модели к формулировке, имеющей конкретное математическое представление. Математическая модель — это уравнения, системы уравнений, системы неравенств, дифференциальные уравнения или системы таких уравнений .
Классификация математических моделей
В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.).
Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация:
● дескриптивные (описательные) модели;
● оптимизационные модели;
● многокритериальные модели;
● игровые модели.
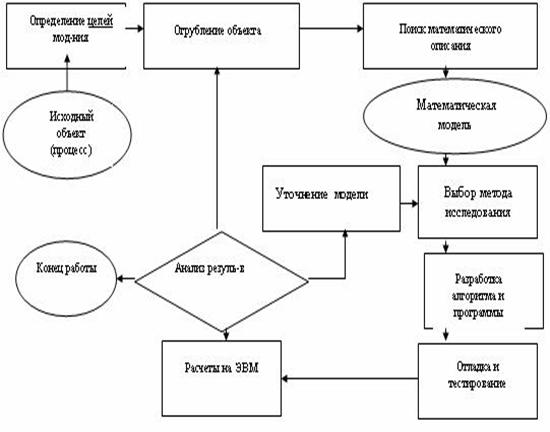
Рис. (1).Блок схема математического моделирования.
2.1 Элементы теории матричных игр
СВЕДЕНИЕ МАТРИЧНОЙ ИГРЫ К ЗАДАЧЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯПредположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
Итак, пусть дана матричная игра с матрицей А порядка m х n. Согласно свойству 7 оптимальные смешанные стратегии х = (х1, ..., хm), y = (y1, ..., yn) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.

![]()

![]()
Разделим все уравнения и неравенства в (1) и (2) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения :
![]()
![]() ,
, ![]()
![]() ,
,
Тогда (1) и (2) перепишется в виде :
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi , чтобы цена игры uбыла максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi ![]() , при которых
, при которых
![]() ,
, ![]() .
. ![]()
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры uбыла наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, ![]() , при которых
, при которых
![]() ,
, ![]() .
. ![]()
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi ![]() , qj
, qj ![]() и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам :
и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам :
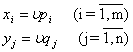
![]()
Пример. Найти решение игры, определяемой матрицей.
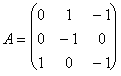
Решение. При решении этой игры к каждому элементу матрицы А прибавим 1 и получим следующую матрицу
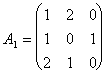
Составим теперь пару взаимно-двойственных задач :
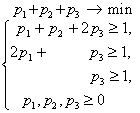
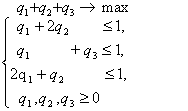
Решим вторую из них
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | a | Отношение |
| -1 | -1 | -1 | 0 | 0 | 0 | 0 | -3 | ||
| q4 | 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | — |
| q5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | — |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | a | Отношение |
| 0 | -1 | 0 | 0 | 1 | 0 | 1 | 1 | ||
| q4 | 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | — |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | |
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | a | Отношение |
| | 0 | 0 | | 1 | 0 | | | ||
| q2 | | 1 | 0 | | 0 | 0 | | | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | | 0 | 0 |
| 0 | 1 | | |
Из оптимальной симплекс-таблицы следует, что![]()
(q1, q2, q3) = (0;![]() ; 1),
; 1),
а из соотношений двойственности следует, что
( p1, p2, p3) = (![]() ; 1; 0).
; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
![]() .
. 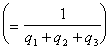 ,
,
а игры с платёжной матрицей А :
![]() .
.
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3) = (uр1; uр2; uр3) = ![]() =
= ![]()
Y = (y1, y2, y3) = (uq1; uq2; uq3) = ![]() =
= ![]() .
.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...





0 комментариев