Навигация
Практическая часть
3. Практическая часть
Постановка задачи: Для производства трёх видов продукции используется три вида сырья. Нормы затрат каждого из видов сырья на единицу продукции данного вида, запасы сырья, а также прибыль с единицы продукции приведены в таблице:
| Продукция/сырьё | А | В | С | Запасы сырья, ед. |
| I | 4 | 2 | 0 | ≤ 19 |
| II | 0 | 1 | 1 | = 8 |
| III | 1 | 2 | 0 | ≤ 24 |
| Прибыль, ден. ед. | 3 | 7 | 2 | ≥ max |
Определить план выпуска продукции для получения максимальной прибыли, чтобы сырьё IIвида было израсходовано полностью. Оценить каждый из видов сырья, используемых для производства продукции.
Вид таблицы по заданию поставленной задачи:
| Вид сырья | Нормы затрат сырья (кг) на единицу продукции | ||
| А | В | С | |
| I II III | 4 0 1 | 2 1 2 | 0 1 0 |
| Цена единицы продукции (руб.) | 3 | 7 | 2 |
Решение поставленной задачи:
Предположим, что производится x1 изделий А, ![]() изделий В и
изделий В и ![]() изделий С. Для определения оптимального плана производства нужно решить задачу, состоящую в максимизации целевой функции
изделий С. Для определения оптимального плана производства нужно решить задачу, состоящую в максимизации целевой функции
3.1.Построим математическую модель задачи:
тогда функция цели:
Z-0 = 3X1 + 7X2 + 2X3 – совокупная прибыль от продажи произведенной продукции, которую требуется максимизировать.
Подсчитаем затраты сырья:
Сырье 1-го типа: 4 х1 + 2 х2 + 0 х3 , по условию затраты не превосходят 19,
Сырье 2-го типа: 0 х1 + 1 х2 + 1 х3, по условию затраты не превосходят 8,
Сырье 3-го типа: 1x1 + 2x2 + 0x3, по условию затраты не превосходят 24.
при следующих условиях:
| 4 | X1 | + | 2 | X2 | + | 0 | X3 | + | X4 | ≤ | 19 |
| 0 | X1 | + | 1 | X2 | + | 1 | X3 | + | X5 | = | 8 |
| 1 | X1 | + | 2 | X2 | + | 0 | X3 | + | X6 | ≤ | 24 |
X1, X2, X3 ≥ 0.
4X1+2X2+X4 ≤ 19
X2 + X3 +X5 = 8
X1+ 2X2+X6 ≤24
3.2 Выбираем метод решения и приводим задачу к каноническому виду:
Пришли к задаче линейного программирования:
припишем каждому из видов сырья, используемых для производства продукции. Тогда общая оценка сырья, используемого на производство продукции, составит:
Получили математическую модель. Необходимо максимизировать функцию цели ↓
Z-0 (x1, x2, x3) = 3X1 + 7X2 + 2X3 → max
Введем дополнительные переменные X4, X5, X6.
| Z-0= | 3 | X1 | + | 7 | X2 | + | 2 | X3 | à(max) |
| при системе ограничений: |
Преобразуем первое ограничение:
| 4 | X1 | + | 2 | X2 | + | 0 | X3 | + | X4 | = | 19 |
| 0 | X1 | + | 1 | X2 | + | 1 | X3 | + | X5 | = | 8 |
| 1 | X1 | + | 2 | X2 | + | 0 | X3 | + | X6 | = | 24 |
Получили задачу:
4X1+2X2+X4 = 19
X2 + X3 +X5 = 8
X1+2X2 +X6 =24
3.3 Решаем задачу путем сведения к задаче линейного программирования:
Xi≥0 ; 0-Z= -3X1- -7X2- -2X3
Приведем задачу к канонической форме.
Задача линейного программирования записана в канонической форме, если она формулируется следующим образом.
Требуется найти вектор ![]() , доставляющий максимум линейной форме
, доставляющий максимум линейной форме
![]()
при условиях
![]()
![]()
где ![]()
Решим задачу симплекс-методом
Строим начальную симплекс-таблицу:
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Свободные члены | ||
| X4 | 4 | 2 | 0 | 1 | 0 | 0 | 19 | ||
| X5 | 0 | 1 | 1 | 0 | 1 | 0 | 8 | ||
| X6 | 1 | 2 | 0 | 0 | 0 | 1 | 24 | ||
| 0-Z | -3 | -7 | -2 | 0 | 0 | 0 | 0 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в строке 0-Z есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в строке 0-Z (-7). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.
Пересчитаем таблицу:
| Базисные переменные | X1 | X2 | X3 | X4 | X5 | X6 | Свободные члены | ||
| X4 | 4 | -2 | -2 | 1 | 0 | 0 | 3 | ||
| X2 | 0 | 1 | 1 | 0 | 1 | 0 | 8 | ||
| X6 | 1 | -2 | -2 | 0 | 0 | 1 | 8 | ||
| 0-Z | -3 | 7 | 5 | 0 | 0 | 0 | 56 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. Так как в строке 0-Z есть отрицательные элементы, то полученное решение не оптимально. Для определения ведущего столбца найдем максимальный по модулю отрицательный элемент в строке 0-Z (-3). А ведущая строка та, у которой наименьшее положительное отношение свободного члена к соответствующему элементу ведущего столбца.
Тогда каноническую форму задачи ЛП можно представить в следующем матричном виде эквивалентном первоначальному:
Z=CX →max,
AX=B,
X≥0.
где 0 - нулевая матрица-столбец той же размерности, что и матрица X.
замечание.
Не ограничивая общности, можно полагать, что свободные члены неотрицательны, т.е. b i ≥ 0, где i =¯1,m (иначе ограничительные уравнения можно умножить на (-1)).
Пересчитаем таблицу:
| Базисные переменные | X4 | X5 | X3 | Свободные члены |
| X1 | 1/4 | -1/2 | -1/2 | 3/4 |
| X2 | 0 | 1 | 1 | 0 |
| X6 | -1/4 | -3/2 | -3/2 | 29/4 |
| 0-Z | 3/4 | 11/2 | 7/2 | 233/4 |
Эта таблица является последней, по ней читаем ответ задачи.
Найдено оптимальное базисное решение:
При котором Z max = 233/4= 58,25 ден. ед.
План производства:
X1 =3/4= 0,75; X2 = 0; X3 = 0; X4 = 3; X5 = 0; X6 = 29/4= 7,25
Соответственно по решению, вычисляем:
Z= 3*0,75+7*0+2*0+3+7,25= 24
Z= 24
Ответ поставленной задачи: План выпуска продукции (Z) для получения максимальной прибыли, при том, что сырьё IIвида было израсходовано полностью равен 24 (Z= 24). Из хода решения задачи по условию мы видим, что оценен каждый из видов сырья, используемых для производства продукции.
Блок-схемы основных процедур при решении и программировании задач
Алгоритм программы → Рис. 1. ↓

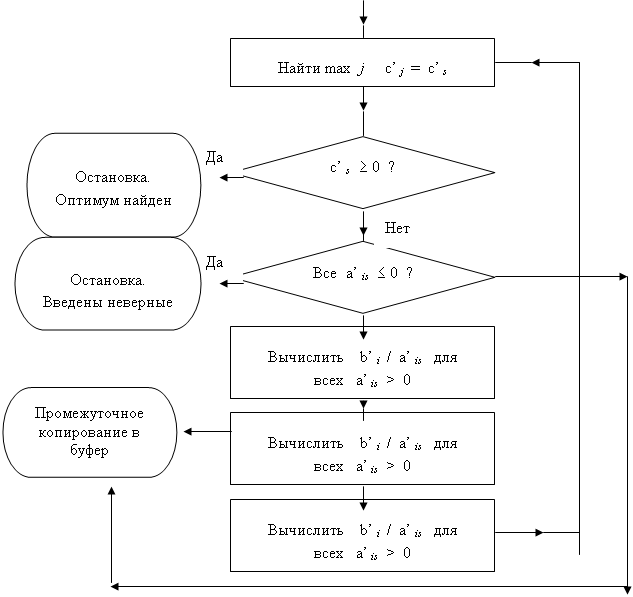
Рисунок 1 –Алгоритм программы для решения ЗЛП (частный случай)
Программа к поставленной задачи (код программы)
Программа - реализующая решение задачи для производства всех видов продукции с использованием всех видов сырья. Нормы затрат каждого из видов сырья на единицу продукции данного вида, запасы сырья, а также прибыль с единицы продукции.
Программа определяет:
План выпуска продукции для получения максимальной прибыли.
1. Описание работы программы, листинг программы
1.1 Обоснование выбора языка
Программа для решения данной задачи составлена на языке C++.C++ представляет собой систему программирования. Как любая подобная система,C++ предназначена для разработки программ и имеет две характерные особенности: создаваемые с ее помощью программы могут работать не только под управлением Windows,но и в системе MS-DOS.
C++ представляет собой наиболее полный пакет объектно-ориентированного программирования. Язык прост в применении и базируется на C#,что упрощает создание программ, людям, знакомым с данным языком.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... области (если допустимая область ограничена и не пуста); 3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи. Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и ...





0 комментариев