Параллельная обработка данных

1.2 Параллельная обработка данных

1.2.1 Принципиальная возможность параллельной обработки

Практически все разработанные к настоящему времени алгоритмы являются последовательными. Например, при вычислении выражения a + b × c , сначала необходимо выполнить умножение и только потом выполнить сложение. Если в электронно-вычислительных машин присутствуют узлы сложения и умножения, которые могут работать одновременно, то в данном случае узел сложения будет простаивать в ожидании завершения работы узла умножения. Можно доказать утверждение, состоящее в том, что возможно построить машину, которая заданный алгоритм будет обрабатывать параллельно.

Можно построить m процессоров, которые при одновременной работе выдают нужный результат за один-единственный такт работы вычислителя.

Такие "многопроцессорные" машины теоретически можно построить для каждого конкретного алгоритма и, казалось бы, "обойти" последовательный характер алгоритмов. Однако не все так просто – конкретных алгоритмов бесконечно много, поэтому развитые выше абстрактные рассуждения имеют не столь прямое отношение к практической значимости. Их развитие убедило в самой возможности распараллеливания, явилось основой концепции неограниченного параллелизма, дало возможность рассматривать с общих позиций реализацию так называемых вычислительных сред – многопроцессорных систем, динамически настраиваемых под конкретный алгоритм.

1.2.2 Абстрактные модели параллельных вычислений

Модель параллельных вычислений обеспечивает высокоуровневый подход к определению характеристик и сравнению времени выполнения различных программ, при этом абстрагируются от аппаратного обеспечения и деталей выполнения. Первой важной моделью параллельных вычислений явилась машина с параллельным случайным доступом (PRAM – Parallel Random Access Machine), которая обеспечивает абстракцию машины с разделяемой памятью (PRAM является расширением модели последовательной машины с произвольным доступом RAM – Random Access Machine). Модель BSP (Bulk Synchronous Parallel, массовая синхронная параллельная) объединяет абстракции как разделенной, так и распределенной памяти. Считается, что все процессоры выполняют команды синхронно; в случае выполнения одной и той же команды PRAM является абстрактной SIMD-машиной, (SIMD – Single Instruction stream/Multiple Data stream – одиночный поток команд наряду со множественным потоком данных), однако процессоры могут выполнять и различные команды. Основными командами являются считывание из памяти, запись в память и обычные логические и арифметические операции.

Модель PRAM идеализирована в том смысле, что каждый процессор в любой момент времени может иметь доступ к любой ячейке памяти (Операции записи, выполняемые одним процессором, видны всем остальным процессорам в том порядке, в каком они выполнялись, но операции записи, выполняемые разными процессорами, могут быть видны в произвольном порядке). Например, каждый процессор в PRAM может считывать данные из ячейки памяти или записывать данные в эту же ячейку. На реальных параллельных машинах такого, конечно, не бывает, поскольку модули памяти на физическом уровне упорядочивают доступ к одной и той же ячейке памяти. Более того, время доступа к памяти на реальных машинах неодинаково из-за наличия кэшей и возможной иерархической организации модулей памяти.

Базовая модель PRAM поддерживает конкурентные (в данном контексте параллельные) считывание и запись. Известны подмодели PRAM, учитывающие правила, позволяющие избежать конфликтных ситуаций при одновременном обращении нескольких процессоров к общей памяти.

Моделировать схемы из функциональных элементов с помощью параллельных машин с произвольным доступом (PRAM) позволяет теорема Брента. В качестве функциональных элементов могут выступать как 4 основных (осуществляющих логические операции NOT, AND, OR, XOR – отрицание, логическое И, логическое ИЛИ и исключающее ИЛИ соответственно), более сложные NAND и NOR (И-НЕ и ИЛИ-НЕ), так и любой сложности.

В дальнейшем предполагается, что задержка (т.е. время срабатывания – время, через которое предусмотренные значения сигналов появляются на выходе элемента после установления значений на входах) одинакова для всех функциональных элементов.

Рассматривается схема из функциональных элементов, соединенных без образования циклов (предполагаем, что функциональные элементы имеют любое количество входов, но ровно один выход – элемент с несколькими выходами можно заменить несколькими элементами с единственным выходом). Число входов определяет входную степень элемента, а число входов, к которым подключен выход элемента – его выходной степенью. Обычно предполагается, что входные степени всех используемых элементов ограничены сверху, выходные же степени могут быть любыми. Под размером схемы понимается количество элементов в ней, наибольшее число элементов на путях от входов схемы к выходу элемента называется глубиной этого элемента (глубина схемы равна наибольшей из глубин составляющих ее элементов).

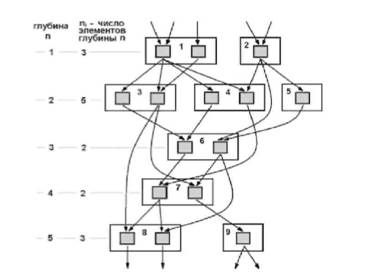
Рисунок 1. Моделирование схемы размера 15, глубины 5 с двумя процессорами с помощью параллельной машины с произвольным доступом (PRAM – машина)

На рисунке 1 приведен результат моделирования схемы размером (общее количество процессоров) n=15 при глубине схемы (максимальное число элементов на каждом из уровней глубины) d=5 с числом процессоров p=2 (одновременно моделируемые элементы объединены в группы прямоугольными областями, причем для каждой группы указан шаг, на котором моделируются ее элементы; моделирование происходит последовательно сверху вниз в порядке возрастания глубины, на каждой глубине по р штук за раз). Согласно теоремы Брента моделирование такой схемы займет не более ceil(15/2+1)=9 шагов.