Навигация
Методи розв’язування задачі
1.2 Методи розв’язування задачі
Розглянемо систему трьох лінійних рівнянь з трьома невідомими:
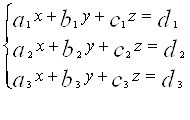 (1)
(1)
Систему (1) можна також записати так:
![]() , і=1, 2, 3.
, і=1, 2, 3.
Тут - деякі задані числа, а x, y, z – невідомі, які потрібно знайти.
Як нам вже відомо, тройка чисел ![]() називаються рішенням системи (1), якщо при підстановці їх в рівняння системи замість x, y і z вийдуть вірні числові рівності.
називаються рішенням системи (1), якщо при підстановці їх в рівняння системи замість x, y і z вийдуть вірні числові рівності.
Розглянемо спочатку випадок, коли всі коефіцієнти рівнянь системи (1) рівні нулю:
![]() і=1, 2, 3.
і=1, 2, 3.
В цьому випадку, якщо всі вільні члени рівнянь системи рівні нулю:
![]() ,
,
то очевидно, люба тройка чисел (x; y; z) являється розв’язком цієї системи. Якщо ж вільні члени рівнянь рівні нулю, то система не має рішень.
Розглянемо тепер більш цікавий випадок, коли не всі коефіцієнти рівнянь системи (1) рівні нулю. Нехай, наприклад, ![]() . Тоді система еквівалентна наступній:
. Тоді система еквівалентна наступній:
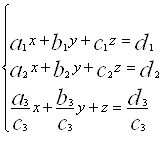
Останнє рівняння цієї системи помножимо на ![]() і вилучаємо почленно із першого рівняння, в результаті получимо рівняння
і вилучаємо почленно із першого рівняння, в результаті получимо рівняння
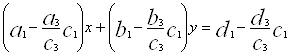 . (2)
. (2)
Аналогічно, помножив останнє рівняння на ![]() і вилучаючи почленно із другого рівняння будемо мати
і вилучаючи почленно із другого рівняння будемо мати
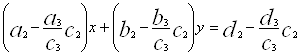 . (3)
. (3)
Очевидно, що система
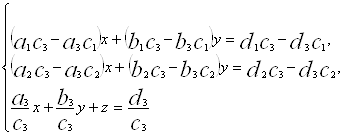 (4)
(4)
у якої перше рівняння виходить із (2), а друге із (3) множенням на![]() , еквівалентна системі (1).
, еквівалентна системі (1).
Таким чином, якщо ![]() 0, то дослідження системи (1) зводиться до дослідження системи двох лінійних рівнянь з двома невідомими:
0, то дослідження системи (1) зводиться до дослідження системи двох лінійних рівнянь з двома невідомими:
 (5)
(5)
Розглянемо спочатку випадок, коли всі коефіцієнти рівнянь системи (5) дорівнюють нулю. Тоді, якщо вільні члени рівнянь системи (5) рівні нулю, то люба пара чисел (x;y) являється рішенням системи (5) і, отже, люба трійка чисел (x;y;z), де ![]()
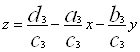 ,
,
являється рішенням системи (1). Якщо ж хоча б у одного із рівнянь системи (5) вільний член не дорівнює нулю, то система (5), то і система (1) не мають рішень.
Розглянемо випадок, коли не всі коефіцієнти рівнянь системи (5) рівні нулю. Нехай, наприклад,
![]()
Перше рівняння системи (5) помножимо на ![]() , друге – на -
, друге – на - ![]() і додамо; після очевидних перетворень отримаємо рівняння
і додамо; після очевидних перетворень отримаємо рівняння
![]()
де
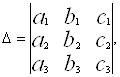
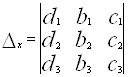
Таким чином, якщо ![]() , то система (5) еквівалентна системі
, то система (5) еквівалентна системі
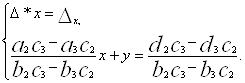
Якщо ![]() , то очевидно, люба пара чисел (x;y), де
, то очевидно, люба пара чисел (x;y), де ![]()
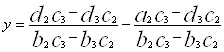 , (6)
, (6)
являється рішенням системи (5).
Із (6) і останнього рівняння системи (4) знаходимо
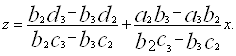 (7)
(7)
Аналогічно, якщо ![]() і
і ![]() , то люба трійка чисел (x;y;z), де
, то люба трійка чисел (x;y;z), де ![]() , а y та z знаходяться в формулах (6) і (7), являється рішенням системи (1).
, а y та z знаходяться в формулах (6) і (7), являється рішенням системи (1).
Якщо ![]() , а
, а ![]() , то система (5), а також і система (1) не мають розв’язків.
, то система (5), а також і система (1) не мають розв’язків.
Нехай тепер ![]() . Тоді
. Тоді
![]() .
.
Підставивши це значення х в друге рівняння системи (5), знайдемо
![]() ,
,
де

Підставивши отримані значення x і y в третє рівняння системи (4), отримаємо
![]() ,
,
де
 .
.
Випливає, якщо ![]() , то система (1) має одне рішення, яке знаходиться за формулами:
, то система (1) має одне рішення, яке знаходиться за формулами:
![]() .
.
Ці формули і називаються формулами Крамера.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... ; b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Показать результат произведения матрицы размерности m х n на вектор- ...
... Найти произведение матриц А = и В = Вычислить значение функции f (x1, x2, x3, x4) = 8 x1 x2 + 4 + 10 x1 (x4)2 в точке (1, 2, 4, 3) Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 16 Объяснить связь базиса и размерности пространства. Дать основные положения задачи ...

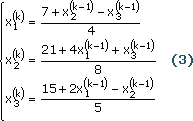
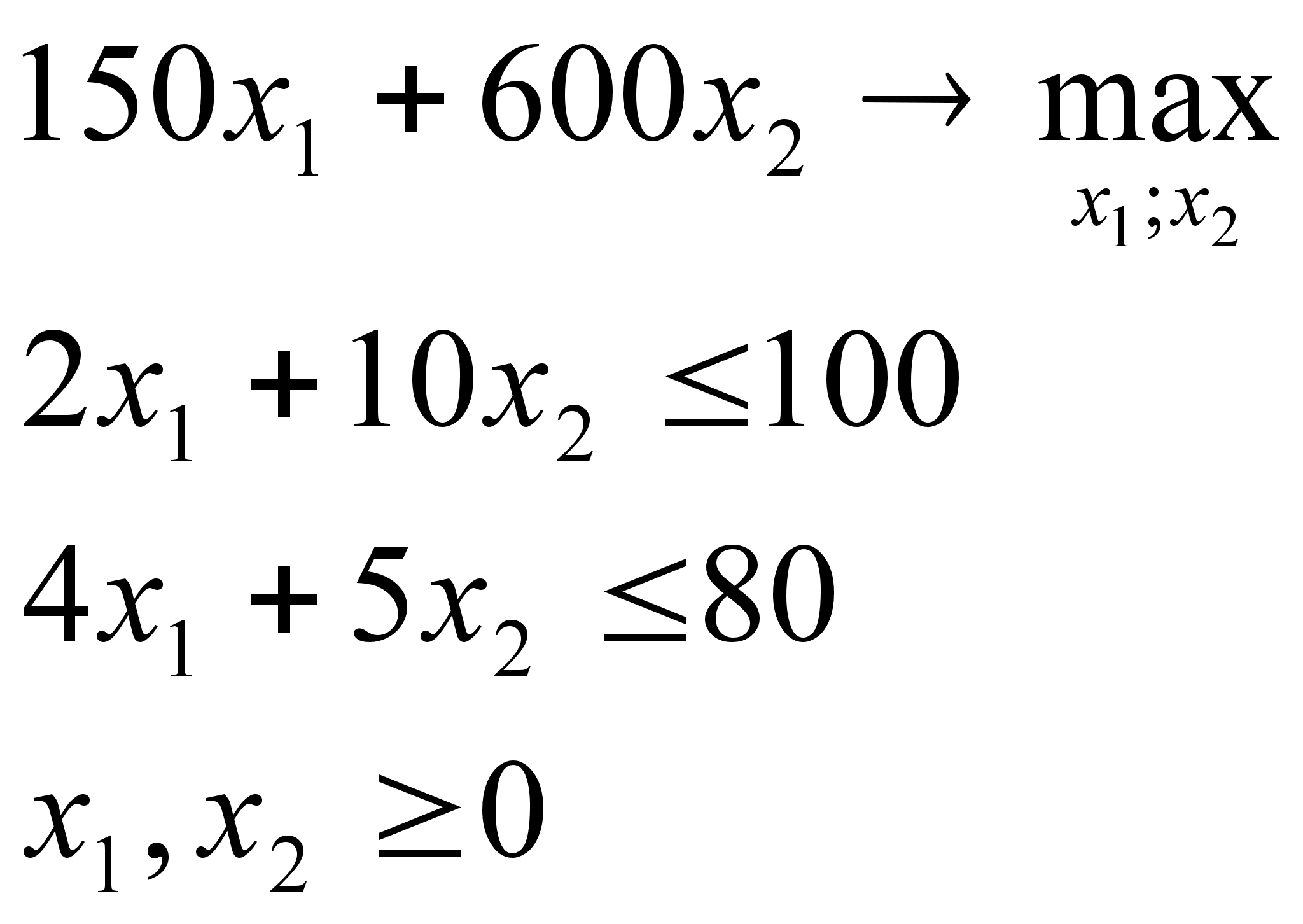
0 комментариев