Навигация
Контрольний приклад та результат машинного експерименту
2.3 Контрольний приклад та результат машинного експерименту
Випробування будь-якої системи є найбільш відповідальний та пов’язаний з найбільшими труднощами і найбільшими втратами часу.
Відладка і тестування – найважливіші етапи життєвого циклу програм. Не можна зробити висновки про правильність виконання програми тільки на підставі того, що вона відкомпільована і видає якісь числові дані, адже в ній все ж ще можуть міститись логічні помилки. Тому необхідно здійснити “ручну” перевірку машинних результатів.
Отже задача: Розв’язати систему лінійних рівнянь з трьома невідомими за допомогою формул Крамера

Знайдемо ![]()
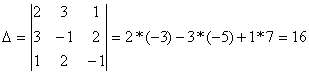
Так, як ![]()
![]() 0, то система має одне рішення.
0, то система має одне рішення.
Тепер знайдемо ![]()
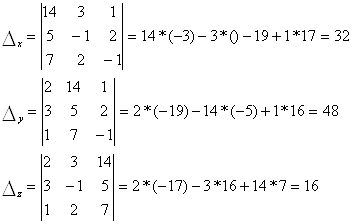
Підставивши знайдені визначники в формули Крамера будемо мати:
![]()
![]()
![]()
Висновки
Зваживши на велику вартість готових формових пакетів, надзвичайно важливо вміти самостійно складати програми для роз’язку окремих типів задач, хоча створення програмного забезпечення зараз являється не областю для програмістів – одинаків, а високотехнічною структурою. Більшість комерційних програмних продуктів являються дуже складними витворами та створені колективами, в які часто входять десятки висококваліфікованих програмістів. Значно більше людей в фірмах – розробниках програмного забезпечення зайнятих організацією продажу, маркетингом, кур’єрством, консультаційним обслуговуванням покупців і т.д. Найбільш відомою є фірма Microsoft, яка займається розробкою програмного забезпечення як для користувацьких програм так і для апаратного програмування.
В даному курсовому проекті розроблено та описано програму отримання результатів розв’язку системи лінійних рівнянь методом Крамера. Програма відладжена з використанням набору текстових даних. Контрольний приклад розроблений вручну для перевірки роботоздатності програми та результат машинного експерименту повністю співпали. Тому можна використовувати дану програму на практиці.
Вибір алгоритмічної мови Паскаль для реалізації поставленої задачі повністю виправдав себе. В процесі розробки програмного забезпечення зроблено висновок про можливість оформлення функції обчислення визначника другого порядку у вигляді програмного модуля, оскільки задача обчислення визначників вищих порядків дуже часто зустрічається при розв’язуванні задач матричної алгебри і може бути зведена до багатократного обчислення визначника другого порядку.
Список використаної літератури
Turbo pascal(учебник) / С.А. Немнюгин – СПБ: Издательство “Питер”, 2000.
М.Я. Ляшенко, М.С. Головань. Чисельні методи. К.:”Либідь”, 1996 – 285 с.
Математика для техникумов – Алгебра и начала анализа.
Додаток 1
(*******************************************************)
(* *)
(* Програма: KRAMER *)
(* *)
(* Автор: Фiлоненко Сеpгiй *)
(* Copyrigth (c) 2003, S.Filonenko *)
(* Дата створення: беpезень 2003 *)
(* *)
(* Використовуванi процедури i функцii: *)
(* vvid *)
(* vyvid *)
(* *)
(********************************************************)
program kramer;
uses graph,crt,dos,zast;
label pt;
var rob:integer;
x1,x2,x3,x4,x5,x6,x7,x8,x9,a,b,c:integer;
d,dx,dy,dz,x,y,z:real;
q:char;
procedure vvid;
begin
closegraph;
clrscr;
textcolor(lightblue);
vid;
gotoxy(9,2); readln (x1);
gotoxy(26,2); readln(x2);
gotoxy(42,2); readln(x3);
gotoxy(57,2); readln(a);
gotoxy(9,4); readln(x4);
gotoxy(26,4); readln(x5);
gotoxy(42,4); readln(x6);
gotoxy(57,4); readln(b);
gotoxy(9,6); readln(x7);
gotoxy(26,6); readln(x8);
gotoxy(42,6); readln(x9);
gotoxy(57,6); readln(c);
end;
procedure vyvid;
begin
closegraph;
clrscr;
textcolor(yellow);
vivyd;
d:=x1*x5*x9+x2*x6*x7+x4*x8*x3-x3*x5*x7-x2*x4*x9-x8*x6*x1;
dx:=a*x5*x9+x2*x6*c+b*x8*x3-x3*x5*c-x2*b*x9-x8*x6*a;
dy:=x1*b*x9+a*x6*x7+x4*c*x3-x3*b*x7-a*x4*x9-c*x6*x1;
dz:=x1*x5*c+x2*b*x7+x4*x8*a-a*x5*x7-x2*x4*c-x8*b*x1;
x:=dx/d;
y:=dy/d;
z:=dz/d;
gotoxy(9,2); writeln (d);
gotoxy(9,4); writeln(dx);
gotoxy(9,6); writeln(dy);
gotoxy(9,8); writeln(dz);
gotoxy(9,10); writeln(x);
gotoxy(9,12); writeln(y);
gotoxy(9,14); writeln(z);
readln;
end;
begin
pt:
rob:=1;
ini;
zas;
while q<>'*' do begin
if keypressed then begin
q:=readkey;
case q of
#80: begin if rob>4 then rob:=1;if rob<4 then rob:=rob+1;end;
#72: begin if rob>1 then rob:=rob-1;if rob<1 then rob:=4; end;
#13: begin if rob=1 then begin about;goto pt;end;
if rob=2 then begin vvid; goto pt; end;
if rob=3 then begin vyvid; goto pt; end;
if rob=4 then halt;
end;
end;
case rob of
1:begin clear;punkt1;end;
2:begin clear;punkt2;end;
3:begin clear;punkt3;end;
4:begin clear;punkt4;end;
end;
end;
end;
end.
Додаток 2
| D | 1.6000000000E+01 |
| DX | 3.2000000000E+01 |
| DY | 4.8000000000E+01 |
| DZ | 1.6000000000E+01 |
| X | 2.0000000000E+00 |
| Y | 3.0000000000E+00 |
| Z | 1.0000000000E+00 |
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... ; b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Показать результат произведения матрицы размерности m х n на вектор- ...
... Найти произведение матриц А = и В = Вычислить значение функции f (x1, x2, x3, x4) = 8 x1 x2 + 4 + 10 x1 (x4)2 в точке (1, 2, 4, 3) Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 16 Объяснить связь базиса и размерности пространства. Дать основные положения задачи ...

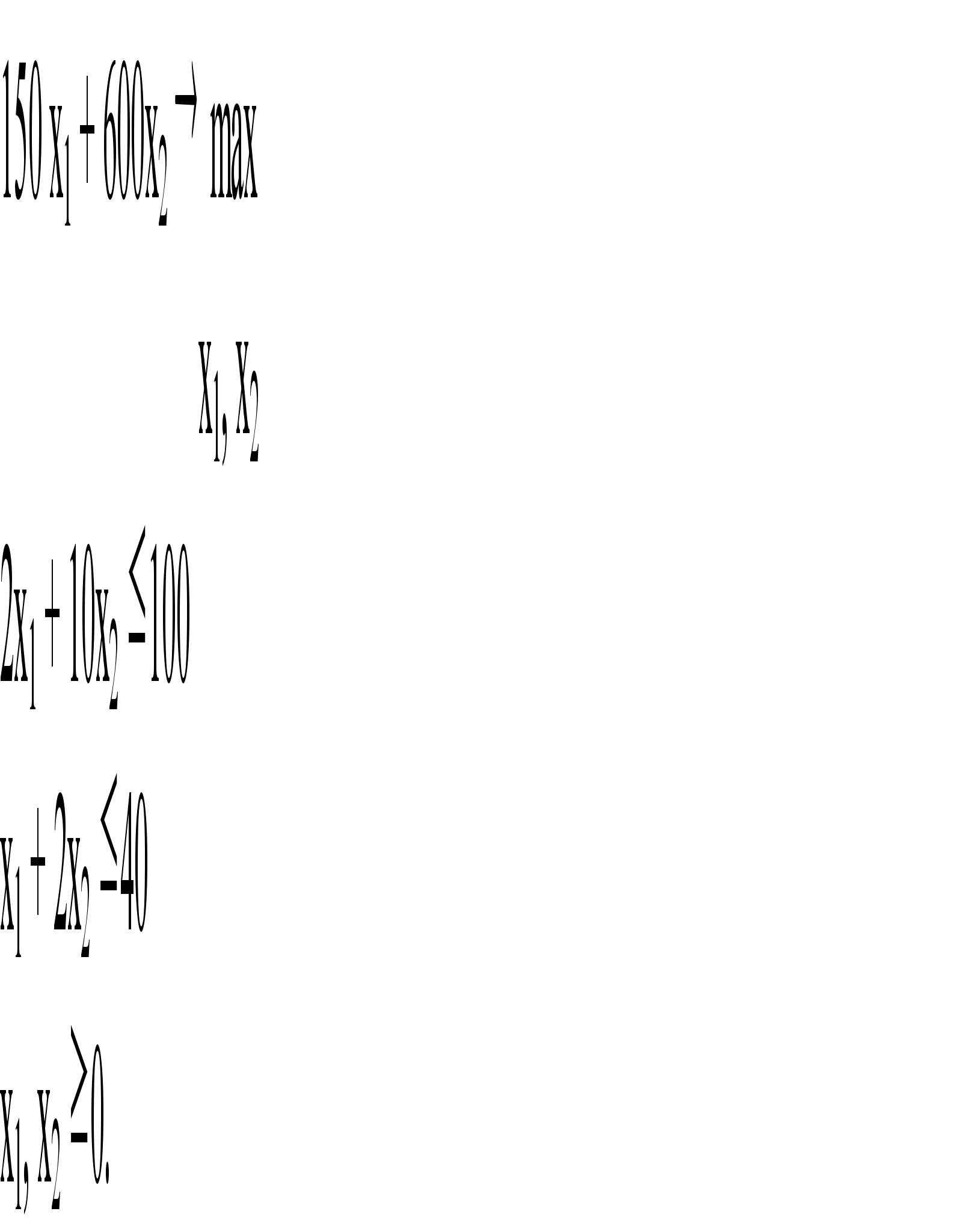
0 комментариев