Навигация
Метод программирования и схем ветвей в процессах решения задач дискретной оптимизации
Содержание
Введение
1. Дискретные оптимизационные задачи
1.1 Постановка задач дискретного программирования
1.2 Алгоритм метода ветвей и границ6
2. Постановка задачи коммивояжера
3. Задача коммивояжера методом динамического программирования
4. Задача коммивояжера методом ветвей и границ
Заключение
Список использованных источников
Введение
Дискретная оптимизация как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Термином "оптимизация" в литературе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего или "оптимального" решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. Поэтому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.
Необходимость принятия наилучших решений так же стара, как само человечество. Испокон веку люди, приступая к осуществлению своих мероприятий, раздумывали над их возможными последствиями и принимали решения, выбирая тем или другим образом зависящие от них параметры - способы организации мероприятий. Но до поры, до времени решения могли приниматься без специального математического анализа, просто на основе опыта и здравого смысла.
Возьмем пример: человек вышел утром из дому, чтобы ехать на работу. По ходу дела ему приходится принять целый ряд решений: брать ли с собой зонтик? В каком месте перейти улицу? Каким видом транспорта воспользоваться? И так далее. Разумеется, все эти решения человек принимает без специальных расчетов, просто опираясь на имеющийся у него опыт и на здравый смысл. Для обоснования таких решений никакая наука не нужна, да вряд ли понадобится и в дальнейшем.
Однако возьмем другой пример. Допусти, организуется работа городского транспорта. В нашем распоряжении имеется какое-то количество транспортных средств. Необходимо принять ряд решений, например: какое количество и каких транспортных средств направить по тому или другому маршруту? Как изменять частоту следования машин в зависимости от времени суток? Где поместить остановки? И так далее.
Эти решения являются гораздо более ответственными, чем решения предыдущего примера. В силу сложности явления последствия каждого из них не столь ясны; для того, чтобы представить себе эти последствия, нужно провести расчеты. А главное, от этих решений гораздо больше зависит. В первом примере неправильный выбор решения затронет интересы одного человека; во втором - может отразиться на деловой жизни целого города.
Наиболее сложно обстоит дело с принятием решений, когда речь идет о мероприятиях, опыта, в проведении которых еще не существует и, следовательно, здравому смыслу не на что опереться, а интуиция может обмануть. Пусть, например, составляется перспективный план развития вооружения на несколько лет вперед. Образцы вооружения, о которых может идти речь, еще не существуют, никакого опыта их применения нет. При планировании приходится опираться на большое количество данных, относящихся не столько к прошлому опыту, сколько к предвидимому будущему. Выбранное решение должно по возможности гарантировать нас от ошибок, связанных с неточным прогнозированием, и быть достаточно эффективным для широкого круга условий. Для обоснования такого решения приводится в действие сложная система математических расчетов.
Вообще, чем сложнее организуемое мероприятие, чем больше вкладывается в него материальных средств, чем шире спектр его возможных последствий, тем менее допустимы так называемые "волевые" решения, не опирающиеся на научный расчет, и тем большее значение получает совокупность научных методов, позволяющих заранее оценить последствия каждого решения, заранее отбросить недопустимые варианты и рекомендовать те, которые представляются наиболее удачными.
1. Дискретные оптимизационные задачи
Дискретные оптимизационные задачи находят широкое применение в различных областях, где используются математические методы для анализа происходящих там процессов. Необходимость решения таких задач приводит к тому, что дискретная оптимизация становится важным элементом образования специалистов, связанных с её применением при решении задач, возникающих в приложениях. Поэтому нам представляется, что технология решения задач дискретного программирования должна стать одной из важных составных частей современного математического образования для специалистов по прикладной математике.
Дискретные оптимизационные задачи можно решать двумя методами: метод дискретного программирования и метод ветвей и границ. Они будут рассмотрены на примере задачи коммивояжера.
1.1 Постановка задач дискретного программированияПод задачей дискретного программирования (дискретной оптимизации) понимается задача математического программирования
F(x0) = min f(x), x є G,
множество допустимых решений которой конечно, т.е. О ≤ |G| = N < ∞, где |G| — число элементов множества G. В силу конечности G все допустимые решения можно пронумеровать: x1, x2, . . . . ., xN, вычислить f(xi), i= 1,2,..., N, и найти наименьшее значение.
Во многих задачах условия дискретности отделены от других условий, т.е. если х = (х1, х2, ... ,хn), то xj є Gj = (х j 1, хj2, ...,хjki), kj > 2. Поэтому N = =![]() =
= ![]() > 2n, отсюда видно, что с ростом числа переменных объем вычислительной работы резко возрастает.
> 2n, отсюда видно, что с ростом числа переменных объем вычислительной работы резко возрастает.
Рассмотрим задачу в виде:
f(x0)=min f(x), x є G, |G|=N < ∞.
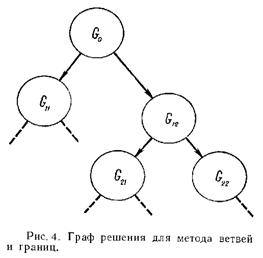
Алгоритм ветвей и границ основан на следующих построениях, позволяющих уменьшить объем перебора.
1. Вычисление оценки. Пусть G' ![]() G, тогда φ(G') называется нижней оценкой, если для любого х є G' выполняется неравенство f(x) ≥ φ(G').
G, тогда φ(G') называется нижней оценкой, если для любого х є G' выполняется неравенство f(x) ≥ φ(G').
Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... и обмена выполняется для значений j от n до 2 последовательно, постепенно уменьшая длину неотсортированной части ряда.4.3 Описание игровых моментов при решении задач При изучении раздела информатики «Алгоритмизация и программирование» написание рабочей программы является конечной целью применения игровых методов. Так, изучение структурного типа данных массив происходит более успешно, если ...
... (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи. 4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы 4.1 Формализация вычислительного процесса и рабочей нагрузки Узел вычислительной системы представляется в виде совокупности оборудования и ...

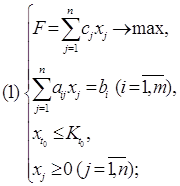
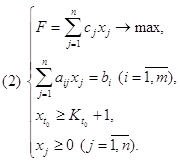
0 комментариев