Навигация
Конечность алгоритма. Конечность алгоритма следует из конечности множества G
8. Конечность алгоритма. Конечность алгоритма следует из конечности множества G.
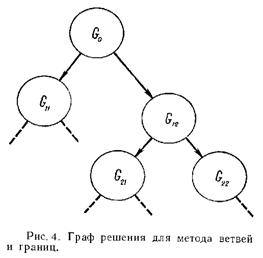
Под методом ветвей и границ понимается алгоритм решения задачи, имеющий древовидную структуру поиска оптимального решения и использующий результаты решения оценочных задач. Древовидная структура называется обычно деревом ветвления.
Эффективность алгоритма ветвей и границ определяется числом решенных задач. Решение задачи состоит из двух основных этапов. На первом этапе находится оптимальное решение (или близкое к нему). На втором этапе производится доказательство оптимальности полученного решения. Второй этап, как правило, оказывается более трудоемким, чем первый. Это означает, что число подзадач, решаемых до получения оптимума, может оказаться существенно меньше числа подзадач, решаемых для доказательства оптимальности.
2. Постановка задачи коммивояжера
Классическая задача коммивояжера (ЗК) формулируется следующим образом: имеется полный взвешенный ориентированный граф без петель G с множеством вершин N = {1, 2,…, n}; веса всех дуг неотрицательны; в этом графе требуется найти гамильтонов цикл минимального веса.
Исходную информацию по ЗК считаем представленной в виде матрицы размера nxn. S = {sij}, где sij – вес дуги (i, j) графа G, i =![]() , j =
, j =![]() , i ≠ j; все элементы главной диагонали матрицы S являются нулями.
, i ≠ j; все элементы главной диагонали матрицы S являются нулями.
В типовой интерпретации вершины 1, 2,…, n графа G – это города. Дуги отображают возможные элементарные переходы. Коммивояжеру, изначально находящемуся в городе 1, необходимо обойти все остальные города, побывав в каждом из них ровно по одному разу, и затем вернуться в город 1. Веса дуг графа трактуются как длины соответствующих элементарных переходов. Требуется найти имеющий минимальную длину допустимый (т.е. удовлетворяющий наложенным требованиям) маршрут коммивояжера. С учетом других возможных интерпретаций, на матрицу S требование симметричности не налагается, не считается обязательным и выполнение неравенства треугольника.
3. Задача коммивояжера методом динамического программирования
Под методом ветвей и границ понимается алгоритм решения задачи, имеющий древовидную структуру поиска оптимального решения и использующий результаты решения оценочных задач. Древовидная структура называется обычно деревом ветвления.
Один из основных алгоритмов решения ЗК основан на принципе динамического программирования. При изложении этого алгоритма будем придерживаться терминологии, соответствующей приведенной типовой интерпретации задачи.
Пусть i – произвольный город (i Î N), а V – любое подмножество городов, не содержащее города 1 и города i. Через М(i, V ) обозначим совокупность путей, каждый из которых начинается в городе i, завершается в городе 1 и проходит в качестве промежуточных только через города множества V, заходя в каждый из них ровно по одному разу. Через В(i, V ) обозначим длину кратчайшего пути множества М(i, V ). Для решаемой задачи В(i, V) – функция Беллмана. Как очевидно, В(1, {2, 3, …, n}) – искомая минимальная длина простого (без самопересечений) замкнутого пути, проходящего через все города.
Если V – одноэлементное множество, V ={j}, где j ≠ 1 и j ≠ i, то совокупность М (i, V) состоит из единственного пути µ = (i, j, 1). Поэтому
![]() i ÎN, j Î {2, 3,…, n}, j ≠ i.(1.1)
i ÎN, j Î {2, 3,…, n}, j ≠ i.(1.1)
Предположим, что значения функции В(i, V ) для всех i ÎN \ {1} и всех возможных k-элементных (k < n – 1) множеств V уже вычислены. Тогда значение В(i, V'), где V' – произвольное (k + 1)-элементное подмножество совокупности N \ {1, i}, вычисляется по формуле
![]() (1.2)
(1.2)
Уравнения (1.1)–(1.12) – рекуррентные соотношения динамического программирования для решения задачи коммивояжера, они обеспечивают реализацию обратного метода Беллмана. Вычислительная сложность задачи равна ![]() ,где С – произвольная константа (С > 0), n – число городов.
,где С – произвольная константа (С > 0), n – число городов.
Пример 1.1 Решить задачу коммивояжера, определяемую матрицей:
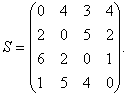
Сначала, пользуясь формулой (1.1), определяем значения В(i, {j}):
В(2, {3}) = 5 + 6 = 11; В(3, {2}) = 2 + 2 = 4; В(4, {2}) = 5 + 2 = 7;
В(2, {4}) = 2 + 1 = 3; В(3, {4}) = 1 + 1 = 2; В(4, {3}) = 4 + 6 = 10.
Далее по формуле (1.2) последовательно получаем (в левой части каждого из ниже записанных равенств выделены те значения параметра j, на которых при подсчете реализуется указанный в правой части (1.2) минимум):
В(2, {3, 4}) = min [s23 + B(3,{4}); s24 + B(4,{3})] = min(5 + 2; 2 + 10)=7;
В(3, {2, 4}) = min [s32 +B(2,{ 4}); s34 + B(4,{ 2})] = min(2 + 3; 1 + 7 )=5;
В(4, {2, 3}) = min [s42 + B(2,{ 3}); s43 + B(3,{ 2})] = min(5 + 11; 4 +4)=8;
В(1, {2, 3, 4}) = min [s12 + B(2,{3,4}) s13 + B(3,{ 2,4}) s14 + B(4,{2,3 })] =
= min (4 +7; 3 +5; 4 + 8 ) = 8.
Итак, оптимальное значение критерия в рассматриваемом примере равно 8.
Выполненные выделения позволяют определить оптимальный маршрут. Он следующий:
1 ® 3 ® 2 ® 4 ® 1.
Для записи соотношений, по которым реализуется прямой метод Беллмана, введем новые обозначения. Пусть М'(V, i) – совокупность путей, каждый из которых начинается в городе 1, проходит в качестве промежуточных только через города подмножества V, заходя в каждый из них ровно по одному разу, и завершается в городе i; здесь, как и ранее, i – произвольный город (i Î N ), а V – любое подмножество N, не содержащее городов 1 и i. Длину кратчайшего пути множества М'(V, i) обозначим В*(V, i). Как очевидно, В*({2, 3, …, n}, 1) – искомая минимальная длина простого (без самопересечений) замкнутого пути, проходящего через все города. Если V – одноэлементное множество, V = {j}, где j ≠ 1 и j ≠ i , то совокупность М'(V, i) состоит из единственного пути µ = (1, j, i). Поэтому
![]()
![]() (1.3)
(1.3)
Предположим, что значения функции В*(V, i) для всех i Î N и всех возможных k-элементных (k < n – 1) множеств V уже вычислены. Тогда значение В*(V', i), где V' – произвольное (k + 1)- элементное подмножество совокупности N \{1, i}, вычисляется по формуле
![]() (1.4)
(1.4)
Уравнения (1.3)–(1.4) – рекуррентные соотношения динамического программирования для решения классической задачи коммивояжера, они обеспечивают реализацию прямого метода Беллмана.
Пример 1.2 Методом прямого счета решить задачу коммивояжера, определяемую матрицей:
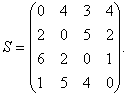
(заметим, что матрица S в данном примере та же, что и в предыдущем).
Сначала, пользуясь формулой (1.3), определяем значения В*( {j }, i):
В*({2}, 3) = 4 + 5 = 9; В*({3}, 2) = 3 + 2 = 5; В*({4}, 2) = 4 + 5 = 9;
В*({2}, 4) = 4 + 2 = 6; В*({3}, 4) = 3 + 1 = 4; В*({4}, 3) = 4 + 4 = 8.
Далее по формуле (1.4) последовательно получаем (в левой части каждого из ниже записанных равенств выделены те значения параметра j, на которых при подсчете реализуется указанный в правой части (1.4) минимум):
В*({2, 3}, 4) = min [B*({2}, 3) + s34; B*({3}, 2) + s24] = min(9 + 1; 5 + 2)= 7;
В*({2, 4}, 3) = min [B*({2}, 4) + s43; B*({4}, 2) + s23] = min(6 + 4; 9 + 5 )= 10;
В*({3, 4}, 2}) = min [B*({3}, 4) + s42; B*({4}, 3) + s32] = min(4 + 5; 8 + 2)= 9;
В*({2, 3, 4}, 1) = min [B*({2, 3}, 4) + s41; B*({2, 4}, 3) + s31; B*({3, 4}, 2) + s21;] = min (7 + 1; 10 +6; 9 + 2 ) = 8.
Итак, оптимальное значение критерия в рассматриваемом примере равно 8.
Выполненные выделения позволяют определить оптимальный маршрут. Он следующий:
1 ® 3 ® 2 ® 4 ® 1.
4. Задача коммивояжера методом ветвей и границ
Другим алгоритмом решения задачи коммивояжера является метод ветвей и границ. В сущности, это некоторая модификация полного перебора решений, оптимизируемая за счет того, что по определенным признакам отсекаются неоптимальные множества перебора.
Формально строится дерево вариантов, начиная от корня. В корне необходимо дать верхнюю и нижнюю оценки. Далее ветвимся. Чем меньший фрагмент дерева придется построить, тем успешнее сработал метод ветвей и границ.
Имеют место следующие определения:
Текущий рекорд – наибольшая из полученных в процессе реализации метода нижних оценок.
Вершина именуется мертвой, если верхняя оценка в ней не превышает текущего рекорда. Выполнять в ней дальнейшее ветвление бесполезно.
Терминальной называется вершина, в которой верхняя и нижняя оценки совпадают.
Вершина, ветвление в которой уже выполнено, называется закрытой.
Вершины, которые не являются мертвыми, терминальными или закрытыми, называются открытыми. Дальнейшее ветвление делаем в них.
Решение заканчивается тогда, когда в нашем дереве вариантов нет открытых вершин. Оптимальным решением будет текущий рекорд.
Верхняя оценка определяется при помощи «жадного» алгоритма.
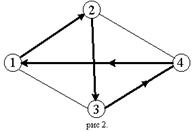
Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния методом выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность (последнее ребро, как правило, самое большое или близко к нему по длине).
Стратегия: «иди в ближайший (в который еще не входил) город». Рассмотрим для примера сеть на рис. 2, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм «иди вы ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
Чтобы вычислить нижнюю оценку, сначала суммируем минимальные элементы по строкам и по столбцам, а затем из полученных сумм выбираем наибольшую, но надо учитывать конфликт.
Пример 2.1 Решить методом ветвей и границ задачу коммивояжера, определяемую матрицей:

1. Вычисляем верхнюю и нижнюю оценки в корне:
Верхнюю оценку подсчитываем, пользуясь, так называемым, «жадным» алгоритмом: каждый переход делаем из текущего в ближайший город. Получаем маршрут:
1 ® 2 ® 4 ® 3 ® 5 ®1
Суммарная стоимость данного маршрута равна 12, она определяет верхнюю оценку в корне.
Чтобы вычислить нижнюю оценку, сначала суммируем минимальные элементы по строкам и по столбцам, а затем из полученных сумм выбираем наибольшую:
По строкам: 2 + 1 + 2 + 2 + 2 = 9
По столбцам: 2 + 2 + 3 + 1 + 2 = 10
Выбираем максимум из значений и выбираем 10.
Проанализируем столбцы: можем сдвинуться на 2 (конфликт). Отсюда нижний предел равен 10 + 2 = 12.
●![]()
|
|

| ||||
| ||||
Далее подсчитываем верхние и нижние оценки для новых вершин:
1 – 2: Верхняя оценка («жадный алгоритм»), определяемая суммарной
стоимостью данного маршрута 1 ® 2 ® 4 ® 3 ® 5 ®1 равна 13. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что идем из 1го города во 2й. Она совпадает с нижней оценкой в корне и равна 12.
1 – 3: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 3 ® 2 ® 5 ® 4®1, равна 16. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что из 1го города идем в 3й. Она равна 2+2+4+ 1+2 = 11 и плюс 2 с учетом конфликта. Итого получаем 13.
1 – 4: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 4 ® 2 ®5® 3 ® 1 равна 24. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что идем из 1го города в 4й. Она равна 18.
1 – 5: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 5 ® 4 ®2® 3 ® 1 равна 23. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что идем из 1го города в 5й. И она равна 16
|
|

|
| |||||||||||||||
|
| ||||||||||||||
| |||||||||||||||
| |||||||||||||||
Проанализируем полученные результаты. Текущий рекорд равен 12.
Переход в вершины 3, 4 и 5 дает ухудшение критерия, поэтому данные вершины именуются мертвыми и ветвление из них далее бессмысленно. Дальше будем ветвиться во 2 и 3 вершинах.
1 – 2 – 3: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 2 ® 3 ® 4 ® 5 ®1 равна 19. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что идем из 1го города во 2й, из 2го в 3й. Она равна 14.
1 – 2 – 4: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 2 ® 4 ® 3 ® 5®1, равна 13. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что из 1го города идем в 2й, из 2го в 4й. Она равна 13.
1 – 2 – 5: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 2 ® 5 ® 4 ® 3®1, равна 16. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что из 1го города идем в 2й, из 2го в 5й. Она равна 12.
| |||
| |||
|
|
|


|

|
 |  |
| |||||||
| |||||||||
|
| |||||
Проанализируем полученные результаты. Переход в вершины 3 и 4 дает ухудшение критерия, поэтому данные вершины именуются мертвыми и ветвление из них далее бессмысленно. Дальше будем ветвиться в 5й вершине.
1 – 2 – 5–3: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 2 ® 5 ® 3 ® 4®1, равна 17. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что из 1го города идем в 2 ® 5® 3. Она равна 15.
1 – 2 – 5–4: Верхняя оценка («жадный алгоритм»), определяемая суммарной стоимостью данного маршрута 1 ® 2 ® 5 ® 4 ® 3®1, равна 16. Нижняя оценка определяется суммой минимальных элементов строк с учетом того, что из 1го города идем в 2й, из 2го в 5й. Она равна 13.
13/12
|
|

|

 | |||
 | |||
![]()

![]()
![]()
|
 | ||||||||
| ||||||||
| ||||||||
В результате решения задачи, дальше ветвиться нам не куда. Запишем оптимальный маршрут коммивояжера:
1 ® 2 ® 5 ® 4 ® 3®1
Таким образом, задача решена.
Заключение
Практика порождает все новые и новые задачи оптимизации, причем их сложность растет. Требуются новые математические модели и методы, которые учитывают наличие многих критериев, проводят глобальный поиск оптимума. Другими словами, жизнь заставляет развивать математический аппарат оптимизации.
Реальные прикладные задачи дискретной оптимизации очень сложны. Современные методы оптимизации далеко не всегда справляются с решением реальных задач без помощи человека. Нет, пока такой теории, которая учла бы любые особенности функций, описывающих постановку задачи. Следует отдавать предпочтение таким методам, которыми проще управлять в процессе решения задачи.
Список использованных источников
1. Беллман, Р. Динамическое программирование – М.: ИЛ, 1960.– 400 с.
2. Беллман, Р. Прикладные задачи динамического программирования – М.: Наука, 1965. – 457 с.
3. Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы. М.: ФИЗМАТЛИТ, 2003. — 240 с.
4. Р. Беллман, С. Дрейфус Прикладные задачи динамического программирования – М., 1965 г., 460 стр.
Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... и обмена выполняется для значений j от n до 2 последовательно, постепенно уменьшая длину неотсортированной части ряда.4.3 Описание игровых моментов при решении задач При изучении раздела информатики «Алгоритмизация и программирование» написание рабочей программы является конечной целью применения игровых методов. Так, изучение структурного типа данных массив происходит более успешно, если ...
... (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи. 4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы 4.1 Формализация вычислительного процесса и рабочей нагрузки Узел вычислительной системы представляется в виде совокупности оборудования и ...

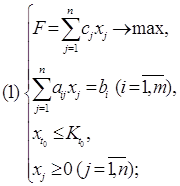
0 комментариев