Навигация
Ветвление (разбиение множества G на подмножества). Положим
2. Ветвление (разбиение множества G на подмножества). Положим
G0 = G и разобьем множество G0 на r1 непересекающихся подмножеств
![]()
![]()
![]()
![]()
![]()
![]() G0 =
G0 = ![]()
![]() , i ≠ j.
, i ≠ j.
Этот шаг алгоритма считаем начальным, имеющим номер 0. Рассмотрим шаг алгоритма с номером k. Пусть ![]()
![]()
![]()
![]() — множества, еще не подвергавшиеся разбиению. Выберем одно из этих множеств
— множества, еще не подвергавшиеся разбиению. Выберем одно из этих множеств ![]() и разобьем его на непересекающиеся подмножества:
и разобьем его на непересекающиеся подмножества: ![]()
Выполним модификацию списка множеств, еще не подвергавшихся разбиению. Заменим множество ![]() множествами
множествами ![]() и множества, еще не подвергшиеся разбиению, переобозначим:
и множества, еще не подвергшиеся разбиению, переобозначим: ![]()
![]()
![]()
![]() .
.
Эти множества образуют список задач для ветвления. Выберем одно из них и снова повторим процедуру разбиения.
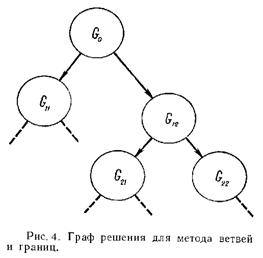
Описанную процедуру разбиения можно представить в виде дерева (рис. 1)
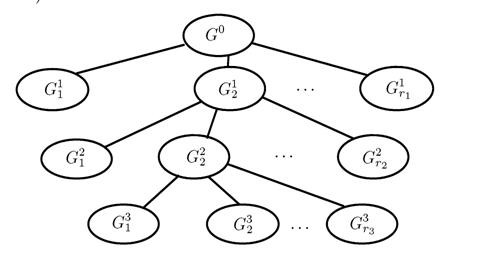
Рис. 1
3. Пересчет оценок. Если G1 ![]() G2, то
G2, то ![]()
Поэтому, разбивая в процессе ветвления подмножество G’ ![]() G на непересекающиеся подмножества
G на непересекающиеся подмножества ![]()
![]()
![]() G's, G' =
G's, G' = ![]() , будем предполагать, что φ(G1’) ≥ φ (G’), причем хотя бы для некоторых номеров i0 выполняется строгое неравенство φ(
, будем предполагать, что φ(G1’) ≥ φ (G’), причем хотя бы для некоторых номеров i0 выполняется строгое неравенство φ(![]() ) ≥ φ (G’).
) ≥ φ (G’).
4. Вычисление планов (допустимых решений). Если на шаге ветвления с номером k известен план хk, на шаге с номером (k + 1) — план хk+1 и если f(xk+1) < f(xk), то план хk забывается и вместо него сохраняется план хk+1. Наилучшее из полученных допустимых решений принято называть рекордом.
5. Признак оптимальности. Пусть G = ![]() . Тогда план
. Тогда план ![]() является оптимальным, т.е.
является оптимальным, т.е. ![]()
![]() , если выполняется условие
, если выполняется условие
f(![]() ) = φ(Gv) ≤ φ(Gi), i=1, 2, . . . . , s.
) = φ(Gv) ≤ φ(Gi), i=1, 2, . . . . , s.
6. Оценка точности приближенных решений. Пусть G = ![]() ,
,
φ0 = ![]() φ(Gj), xk — рекорд; тогда имеет место следующее неравенство:
φ(Gj), xk — рекорд; тогда имеет место следующее неравенство:
φ0 ≤ f(x0) ≤ f(xk).
Разность ∆ = f(xk) - φ0 является оценкой гарантированного отклонения рекорда хk от оптимума х0. Из приведенного неравенства следует, что для ветвления необходимо выбрать множество с минимальным значением нижней оценки.
7. Правило отсева. Пусть снова G = ![]() , x0 — оптимум, хk — рекорд. Если φ(Gr) > f(xk), то множество Gr можно отсеять, т.е. исключить из дальнейшего рассмотрения, так как оно не может содержать оптимальных решений. Действительно, пусть x є G; тогда в силу определения оценки f(x) ≥ φ(G') имеем f(x) ≥ φ(Gr) > f(xk) ≥ f(x0).
, x0 — оптимум, хk — рекорд. Если φ(Gr) > f(xk), то множество Gr можно отсеять, т.е. исключить из дальнейшего рассмотрения, так как оно не может содержать оптимальных решений. Действительно, пусть x є G; тогда в силу определения оценки f(x) ≥ φ(G') имеем f(x) ≥ φ(Gr) > f(xk) ≥ f(x0).
Правило φ(Gr) > f(xk) гарантирует, что в процессе работы алгоритма ни одно из подмножеств Gr, в которых содержится точное решение x0, не будет отсеяно. Более сильное правило φ(Gr) ≥ f(xk) гарантирует, что хотя бы одно оптимальное решение будет найдено, оно и применяется при практическом решении задач.
Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... и обмена выполняется для значений j от n до 2 последовательно, постепенно уменьшая длину неотсортированной части ряда.4.3 Описание игровых моментов при решении задач При изучении раздела информатики «Алгоритмизация и программирование» написание рабочей программы является конечной целью применения игровых методов. Так, изучение структурного типа данных массив происходит более успешно, если ...
... (Балаша-Фора-Мальгранжа, Черенина, Джефферсона, Хиллиера и др.) являются модификациями метода ветвей и границ с учётом специфики условий задачи. 4. Построение оптимальной последовательности заданий на обработку в узле вычислительной системы 4.1 Формализация вычислительного процесса и рабочей нагрузки Узел вычислительной системы представляется в виде совокупности оборудования и ...

0 комментариев