Методические проблемы изучения алгоритмов работы с величинами

План.

Введение

Понятие алгоритма

ЭВМ — исполнитель алгоритмов

Характеристики величин

Действия над величинами.

Свойства алгоритмов

Алгоритмы работы с величинами

Список литературы

Практическая часть

Заключение

Вывод

Приложения

Введение

Понятие алгоритма является одним из основных понятий современной математики. Еще на самых ранних ступенях развития математики (Древний Египет, Вавилон, Греция) в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам и инструкциям. Со временем все такие процессы в математике получили название алгоритмов (алгорифмов).

Термин алгоритм происходит от имени средневекового узбекского математика Аль-Хорезми, который еще в IX в. (825) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом.

С 1747 г. вместо слова алгоризм стали употреблять алгорисмус,

смысл которого состоял в комбинировании четырех операций арифметического исчисления сложения, вычитания, умножения, деления.

К 1950 г. алгорисмус стал алгорифмом. Смысл алгорифма чаще всего связывался с алгорифмами Евклида — процессами нахождения наибольшего общего делителя двух натуральных чисел, наибольшей общей меры двух отрезков и т.п. Под алгоритмом понимали конечную последовательность точно сформулированных правил, которые позволяют решать те или иные классы задач. Такое определение алгоритма не является строго математическим, так как в нем не содержится точной характеристики того, что следует понимать под классом задач и под правилами их решения. Первоначально для записи алгоритмов пользовались средствами обычного языка (словесное представление алгоритмов).

 Исполнителем алгоритмов работы с величинами может быть человек или специальное техническое устройство, например компьютер. Такой исполнитель должен обладать памятью для хранения величин. Величины бывают постоянными и переменными.

Понятие алгоритма.

Понятие алгоритма является одним из основных понятий современной математики. Еще на самых ранних ступенях развития математики (Древний Египет, Вавилон, Греция) в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам и инструкциям. Со временем все такие процессы в математике получили название алгоритмов (алгорифмов).

Термин алгоритм происходит от имени средневекового узбекского математика Аль-Хорезми, который еще в IX в. (825) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом.

С 1747 г. вместо слова алгоризм стали употреблять алгорисмус,

смысл которого состоял в комбинировании четырех операций арифметического исчисления сложения, вычитания, умножения, деления.

К 1950 г. алгорисмус стал алгорифмом. Смысл алгорифма чаще всего связывался с алгорифмами Евклида - процессами нахождения наибольшего общего делителя двух натуральных чисел, наибольшей общей меры двух отрезков и т.п. Под алгоритмом понимали конечную последовательность точно сформулированных правил, которые позволяют решать те или иные классы задач. Такое определение алгоритма не является строго математическим, так как в нем не содержится точной характеристики того, что следует понимать под классом задач и под правилами их решения. Первоначально для записи алгоритмов пользовались средствами обычного языка (словесное представление алгоритмов).

Уточним понятие словесного представления алгоритма на примере нахождения произведения п. Натуральных чисел - факториал числа п (с =n!), т.е. вычисления по формуле с = 1*2*3*4*...*n. Этот процесс может быть записан в виде следующей системы последовательных указаний (пунктов):

1. Полагаем с равным единице и переходим к следующему пункту.

2. Полагаем i равным единице и переходим к следующему пункту.

3. Полагаем с = i*c и переходим к следующему пункту.

4. Проверяем, равно ли ; числу п. Если i= п , то вычисления прекращаем. Если i < п , то увеличиваем i на единицу и переходим к пункту 3.

Рассмотрим еще один пример алгоритма - нахождение наименьшего числа М в последовательности из п чисел a1,a2,...an ( n = 0). Прежде чем записать словесный алгоритм данного примера, детально рассмотрим сам процесс поиска наименьшего числа. Будем считать, что процесс поиска осуществляется следующим образом. Первоначально в качестве числа М принимается A1, т. е полагаем М =A1 после чего М сравниваем с последующими числами последовательности, начиная с A2, если М <A2, то М сравнивается с A3, если М <A3, то М сравнивается с A4, и так до тех пор, пока найдется число Ai<М. Тогда полагаем М = Ai и продолжаем сравнение с М последующих чисел из последовательности, начиная с Ai+1 и так до тех пор, пока не будут просмотрены все п чисел. В результате просмотра всех чисел М будет иметь значение, равное наименьшему числу из последовательности (I- текущий номер числа). Этот процесс может быть записан в виде следующей системы последовательных указаний:

1. Полагаем i= 1 и переходим к следующему пункту.

2. Полагаем М=Ai и переходим к следующему пункту.

3. Сравниваем i с п; если i<п, переходим к 4 пункту, если i=п, процесс поиска останавливаем.

4. Увеличиваем, i на 1 и переходим к следующему пункту.

5. Сравниваем Ai с М. Если М<Ai, то переходим к пункту 3, иначе (М>А) переходим к пункту 2.

В первом алгоритме в качестве элементарных операций используются простейшие арифметические операции умножения, которые могли бы быть разложены на еще более элементарные операции. Мы такого разбиения не делаем в силу простоты и привычности, арифметических правил.

Алгоритмы, в соответствии с которыми решение поставленных задач сводится к арифметическим действиям,называются численными алгоритмами.

Алгоритмы, в соответствии с которыми решение поставленных задач сводится к логическим действия, называются логическими алгоритмами. Примерами логических алгоритмов могут служить алгоритмы поиска минимального числа, поиска пути на графе, поиска пути в лабиринте и др.

Алгоритмом, таким образом, называется система четких однозначных указаний, которая определяет последовательность действий над некоторыми объектами и после конечного числа шагов приводит к по лучению требуемого результата.

ЭВМ — исполнитель алгоритмов.

Обсуждение методических вопросов изучения темы «Алгоритмы работы с величинами» буде проводить в программистском аспекте. Составление любой программы для ЭВМ начинается с построения алгоритма. Как известно, всякий алгоритм (программа) составляется для конкретного исполнителя, в рамках его системы команд. О каком же исполни теле идет речь в теме «программирование для ЭВМ»? Ответ очевиден: исполнителем является компьютер. Точнее говоря, исполнителем является комплекс «ЭВМ + система программирован и (СП)». Программист составляет программу на том языке, на который ориентирована СП. Иногда в литературе по программированию такой комплекс называют «виртуальной ЭВМ». Например, компьютер с работающей системой программирования на Бейсике называют «Бейсик-машина»; компьютер с работающей системой программирования на Паскале называют «Паскаль-машина и т. п. Схематически это изображено на рис. 1.

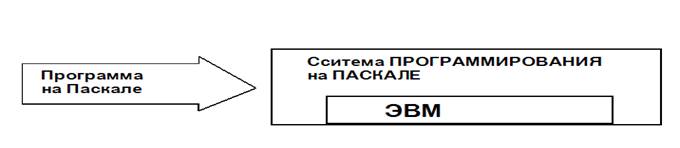Рис. 1. Взаимодействие программиста с компьютером

Входным языком такого исполнителя является язык програм­мирования Паскаль. При изучении элементов программирования в базовом курсе необходимо продолжать ту же структурную линию, которая была обнаружена в алгоритмическом разделе. Поэтому при выборе языка и программирования следует отдавать предпочтение языкам структурного программирования. Наиболее подходящим из них для обучения является Паскаль.

Процесс программирования делится на три этапа:

1 составление алгоритма решения задачи;

2 составление программы на языке программирования;

3 отладка и тестирование программы.

Дня описания алгоритмов работы с величинами следует, как раньше, использовать блок-схемы и учебный алгоритмический язык. Описание алгоритмов должно быть ориентировано на со структурным входным языком, независимо от того, язык программирования будет использоваться на следуе­м этапе.

 Характеристики величин.

Теперь обсудим специфику понятия исипчины и методические проблемы раскрытия этого понятия.

Компьютер работает с информацией. Информация, обрабатываемой компьютерной программой, называется данными. Величина — это шильный информационный объект, отдельная единица данных. Команды II компьютерной программе определяют действия, выполняемые над величинами. По отношению к программе данные делятся на исход­ные, результаты (окончательные данные) и промежуточные дан­ные, которые получаются в процессе вычислений (рис. 2).

Рис. 2. Уровни данных относительно программы

Например, при решении квадратного уравнения: ах² + bх + с = 0 исходными данными являются коэффициенты а, Ь, с; результатами - корни уравнения: х_1, х₂; промежуточным данным - дискриминант уравнения: D = Ь² - 4ас.

Важнейшим понятием, которое должны усвоить ученики, яв­ляется следующее: всякая величина занимает свое определенное меню в памяти ЭВМ - ячейку памяти. В результате в сознании уче­ников должен закрепиться образ ячейки памяти, сохраняющей величину. Термин «ячейка памяти» рекомендуется употреблять и в дальнейшем для обозначения места хранения величины. У всякой величины имеются три основных характеристики: имя, точение и тип. На уровне машинных команд всякая величина идентифицируется адресом ячейки памяти, в которой она хранится, а все значение - двоичный код в этой ячейке. В алгоритмах и языках программирования величины делятся на константы и переменные.

Константа - неизменная величина и в алгоритме она представляется собственным значением, например: 15, 34.7, true и пр. Переменные величины могут изменять свои значения в ходе выполнения программы и представляются символическими именами идентификаторами, например: X, S2, соd15 и пр. Однако ученики должны знать, что и константа, и переменная занимают ячейку памяти, а значение этих величин определяется двоичным кодом и этой ячейке.

Теперь о типах величин - типах данных. С понятием типа данных ученики уже могли встречаться, изучая базы данных и электронныетронные таблицы. Это понятие является фундаментальным, или программирования. Поэтому в данном разделе базового курса происходит возврат к знакомому разговору о типах, но на новом уровне.

В каждом языке программирования существует своя концепция типов данных, своя система типов. Однако в любой язык минимально-необходимый набор основных типов данных, n которому относятся следующие: целый, вещественный, логическая и символьный. С типом величины связаны три ее свойства: множество допустимых значений, множество допустимых операции, форма внутреннего представления

Типы констант определяются по контексту (т.е. по форме записи » тексте), а типы переменных устанавливаются в описании.

 Есть еще один вариант классификации данных: классификация по структуре. Данные делятся на простые и структурированные. Для простых величин (их еще называют скалярными) справедливо утверждение: одна величина - одно значение. Для структурирование одна величина - множество значений. К структурированным величинам относятся массивы, строки, множества и др. В разделе базоаого курса «Введение в программирование» структурирование величины могут не рассматриваться.

Действия над величинами.

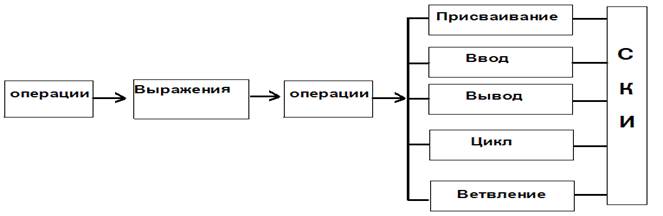
Определяемые алгоритмом (прогромный), основываются на следующей иерархии понятий: операция - выражение - команда, или оператор - система

команд (рис. 3).

 Рис. 3. Средства выполнения действий над величинами

Операция - простейшее законченное действие над данными. Операции для основных типов данных перечислены в приведен­ной выше таблице.

Выражение - запись в алгоритме (программе), определяю­щий последовательность операций для вычисления некоторой ве­личины.

Команда - входящее в запись алгоритма типовое предписание исполнителю выполнить некоторое законченное действие. Команды присваивания, ввода, вывода называются простыми командами; команды цикла и ветвления - составными, или структурными, В языках программирования строго определены правила записи операций, выражений, команд. Эти правила составляют синтаксис языка. При описании алгоритма в виде блок-схемы или на алгоритмическом языке строгое соблюдение синтаксических правил не является обьязательным. Программист пишет алгоритм для себя как предварительный этап работы перед последующим составлением программы. Поэтому достаточно, чтобы смысл алгоритма был понятен его автору. В то же время в учебном процессе требуется некоторая унификация способа описания алгоритма для взаимопонимания. Однако еще раз подчеркнем, что эта унификация не так жестко формализована, как в языках программирования.

Не следует требовать от учеников строгости в описаниях алгоритмов с точностью до точки или запятой. Например, если для команда в алгоритме на АЯ записывается в отдельной строке, то совсем не обязательно в конце ставить точку с запятой. В качестве знака умножения можно употреблять привычные из математики тики точку или крестик, но можно и звездочку - характерную для языков программирования. Но следует иметь в виду, что и описаниях алгоритмов нужно ориентироваться только на тот отбор операций и команд, который имеется у исполнителя. Не нужно употреблять операции или функции, которые нет в используемом языке программирования. Например, если составляется алгоритм для дальнейшего программирования Бейсике, то в нем можно использовать операцию возведения и степень в виде: х⁵ или х^5, потому что в языке программировании есть эта операция (пишется Х^{^}5). Если же программа будет записываться на Паскале, в котором отсутствует операция возведении в степень, то и в алгоритме не следует ее употреблять; нужно писать так: х*х*х*х*х. Возведение в большую целую чисел, например в 20, 30-ю, следует производить циклическим умножением. Возведение в вещественную степень организуется через функции ехр и ln: х^у= е^уlпх => ехр(y*ln(x)).

Узловыми понятиями в программировании являются понятии переменной и присваивания. О переменной уже говорилось выше, Процесс решения вычислительной задачи -это процесс последовательного изменения значений переменных. В итоге в определенных переменных получается искомый результат. Переменная получает определенное значение в результате присваивания. Из числа команд, входящих в представленную выше СКИ, присваивание выполняют команда ввода и команда присваивания. Есть еще трети способ присваивания - передача значений через параметры под программ. Но о нем мы здесь говорить не будем. Педагогический опыт показывает, что в большинстве случае непонимание некоторыми учениками программирования происходит от непонимания смысла присваивания. Поэтому учителям рекомендуется обратить особое внимание на этот вопрос.

Команда присваивания имеет следующий вид:

<переменная> := <выражение>

Знак «:=» надо читать как «присвоить». Это инструкция, который обозначает следующий порядок действий:

1) вычислить выражение;

2) присвоить полученное значение переменной.

Обратите внимание учеников на то, что команда выполняется право или налево. Нельзя путать команду присваивания с математическим равенством! Особенно часто путаница возникает в тех случаях, когда в качестве знака присваивания используется знак «=» учитель читает его как «равно». В некоторых языках программирования знак «=» используется как присваивание, например, в идейке и Си. В любом случае надо говорить «присвоить».

Ученикам, отождествляющим присваивание с равенством, совершенно непонятна такая команда: Х= Х+ 1. Такого математического равенства не может быть! Смысл этой команды следует, и исполнять так: к значению переменной X прибавляется единица, и культура присваивается этой же переменной X. Иначе говоря, данная команда увеличивает значение переменной X на единицу.

Под вводом в программировании понимается процесс переда­чи данных с любого внешнего устройства в оперативную память. В рамках введения в программирование можно ограничиться узким пониманием ввода как передачи данных с устройства ввода клавиатуры в ОЗУ. В таком случае ввод выполняется компьюте­ром совместно с человеком. По команде ввода работа процессора прерывается и происходит ожидание действий пользователя; пользователь набирает на клавиатуре вводимые данные и нажи­мист на клавишу <ВВОД>; значения присваиваются вводимым переменным.

Вернемся к вопросу об архитектуре ЭВМ - исполнителе вы­числительных алгоритмов. Как известно, одним из важнейших практических принципов в методике обучения является прин­цип наглядности. За каждым изучаемым понятием в сознании уче­ника должен закрепиться какой-то визуальный образ. Успешность поучения алгоритмизации при использовании учебных материалов объясняется именно наличием таких образов как (Черепашки, Кенгуренка и др.). Можно еще сказать так: архитектура исполнителей является наглядной, понятной ученикам. Ис­полнителем вычислительных алгоритмов (алгоритмов работы с величинами) является компьютер. Успешность освоения програм­мирования для ЭВМ во многом зависит от того, удастся ли учителю создать в сознании учеников наглядный образ архитектуры компьютера-исполнителя. Работа с реализованными в виде испол­нителей учебными компьютерами («УК Нейман», «Кроха», «Ма­лютка» и др.) помогает решению этой задачи. Составляя вычис­лительные алгоритмы, программы на языках высокого уровня, ученики в своем понимании архитектуры могут отойти от деталей ячеек памяти, типов регистров процессора и т.п. подробностей, но представление об общих ЭВМ по выполнению программы у них должно остаться. Вот как должен представлять себе ученик выполнение алгоритма сложения двух чисел (рис. 11.8):

Алг сложения

цел А, В, С

нач

Ввод А  

Ввод В

С:=А+В

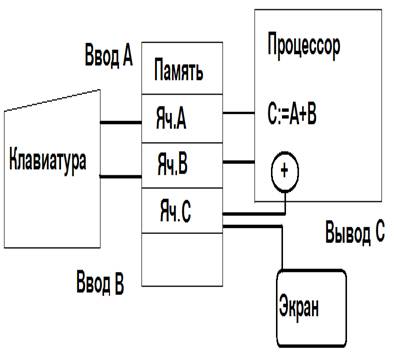
Рис. 11.8. Исполнение компьютером вычислительного алгоритма.

Эффективным методическим средством, позволяющим достичь, понимания программирования, является ручная трассировка алгоритмов, которая производится путем заполнения трассировочной таблицы.