Методы и алгоритмы компьютерного решения дифференциальных уравнений

Методы и алгоритмы компьютерного решения дифференциальных уравнений

Введение

Для того, чтобы описать динамику различных процессов, протекающих в природных и в технических системах, составляют, опираясь на физические законы, дифференциальные уравнения. Так, в частности, приходится поступать при исследовании функционирования автоматических систем; работы судовых энергетических комплексов, электрических агрегатов, судовых вспомогательных механизмов, систем навигации и т.д. В ряде случаев эти уравнения допускают линеаризацию и могут быть записаны в виде:

,

где y(t) – неизвестная функция, a₀, a₁,...a_n – постоянные коэффициенты, а j(x) – некоторая известная функция независимого аргумента t, которая обычно выражает внешнее воздействие, оказываемое на систему.

1. Цель контрольной работы

Приобретение навыков алгоритмизации и программирования задач численного интегрирования обыкновенных дифференциальных уравнений и систем с последующим моделированием результатов на персональном компьютере и представлением их в виде таблиц и графиков.

В результате выполнения контрольной работы студент обязан:

1.   Научиться решать линейные дифференциальные уравнения численными и символьными методами в рамках пакета компьютерной математики MathCAD.

2.   Ознакомиться с основными алгоритмами существующих компьютерных методов.

3.   Определить точность этих методов путем сравнения результатов, получаемых путем приближенного и аналитического решений.

2. Аналитические методы

Общее решение дифференциального уравнения n-го порядка – неизвестная функция y(t) – содержит n произвольных постоянных. Их можно определить, зная начальные условия, накладываемые на неизвестную функцию и на ее производные вплоть до (n-1)-порядка включительно. Аналитически (в символьном виде) такие уравнения решают классическим и операционным методами.

 

2.1 Классический метод

 

В ограниченном числе случаев вида левой части (1) допускает такое преобразование, которое позволяет найти решение путем непосредственного интегрирования, однако в общем случае порядок решения – иной.

Решение неоднородного дифференциального уравнения (с ненулевой правой частью) является суммой общего решения соответствующего однородного дифференциального уравнения y₁(t) и частного решения y₂(t) неоднородного дифференциального уравнения (1).

Решение однородного уравнения ищем в виде: . Подстановка его в дифференциальное уравнение приводит к характеристическому алгебраическому уравнению n-ного порядка:

,

которое имеет n корней – . В частном случае отсутствия кратных корней общее решение может быть записано в виде:

,

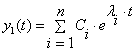где С_i – произвольные постоянные, которые находятся из начальных условий.

Имеются правила, позволяющие определить вид y₂(t) частного решения в зависимости от вида правой части – функции j(t). Последующая подстановка общего решения в исходное дифференциальное уравнение позволяет найти неопределенные константы C_i в выражении для y₁(t).

«Классический» метод анализа процессов в настоящее время используется только в случае простейших систем, поскольку необходимость нахождения частного решения часто приводит к сложным преобразованиям, а также, кроме решения характеристического уравнения дополнительно необходимо составить и решить n уравнений для определения постоянных интегрирования.

 

2.2 Метод операционного исчисления

Суть метода состоит в проведении интегрального преобразования Лапласа функции, входящей в состав дифференциального уравнения, по правилу:

,

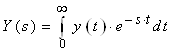где s = a+ j×b – комплексная переменная величина.

Это преобразование сопоставляет функции действительного переменного функцию комплексного переменного. При этом для линейных дифференциальных уравнений существует изоморфизм (взаимно-однозначное соответствие) между функциями-оригиналами, входящими в уравнение, и их изображениями (образами Лапласа).

Преобразование Лапласа можно выполнить, используя блок символьных вычислений MathCAD. Этот же блок позволяет выполнить и обратное преобразование Лапласа, в соответствии с соотношением:

,

где , т. е. интегрирование проводится по прямой, лежащей в плоскости комплексного переменного s и проходящей параллельно мнимой оси jw на расстоянии s от нее, при этом Лаплас образ Y(s) должен иметь особенности слева от этой линии.

Преобразование Лапласа сводит дифференцирование функции оригинала к умножению ее образа на комплексную переменную s, поэтому решение дифференциального уравнения в пространстве оригиналов сводится к решению алгебраического уравнения в пространстве изображений.

Порядок решения дифференциального уравнения с помощью операционного исчисления представляется следующим:

-          выполняя преобразование Лапласа левой и правой части дифференциального уравнения, учитываем начальные условия и переходим от дифференциального уравнения для функции оригинала y(t) к алгебраическому уравнению для Лаплас образа – Y(s) ;

-          решая алгебраическое уравнение, находим в пространстве изображений в явном виде выражение для Y(s);

-          выполняя обратное преобразование мы находим неизвестную функцию y(t).

Все этапы этой процедуры могут быть автоматизированы и выполнены в рамках пакета MathCAD (пример 1).

Следует заметить, что пакет MathCAD далеко не всегда способен выполнить в символьной форме результат обратного Лаплас преобразования. Дело в том, что в блок символьных преобразований пакета заложены правила выполнения данной процедуры для выражений записанных в виде элементарных дробей. Поэтому Лаплас образ предварительно разлагается на элементарные дроби. Однако, если корни полинома в знаменателе представляются в виде комбинации сложных радикалов, то MathCAD «отказывается» работать. В этом случае ему необходимо «помочь» врукопашную выполнив разложения полинома в знаменателе в соответствии с соотношением:

 

,

где s₁, s₂,…s_n – корни уравнения . В примере 1 рассмотрено выполнение обратного преобразования Лапласа и для такого случая.

Рассмотренная методика нахождения аналитического решения дифференциальных уравнений может быть распространена на задачу решения системы дифференциальных уравнений. В этом случае необходимо решить не одно алгебраическое уравнение для Лаплас-образов, а систему алгебраических уравнений с помощью той же процедуры блока решений Given – Find. Отметим, что в отличие от систем компьютерной математики Mathematica 2.2.2 и Maple V R3/R4, которые легко позволяют аналитически решить линейное дифференциальное уравнение с помощью встроенных средств. Система MathCAD предполагает «ручные процедуры» запуска прямого преобразования Лапласа, составления по его результатам алгебраического уравнения и, после его решения, запуска процедуры обратного преобразования Лапласа.