Метод композиции

4. Метод композиции

Метод композиции основывается на представлении плотности вероятности fη (x) по формуле полной вероятности:

 

fη (x)= (27)

 

Где H(z)=P(ζz)– интегральная функция распределения случайной величины ζ;

P(x/z )- условная плотность вероятности.

Переходя к дискретной форме, интеграл заменяется на сумму и тогда получаем

 

fη (x)=P_j*f_j (x) (28)

где P_j=1(29)

f_j(x) -условная плотность вероятности

Таким образом, для любой заданной плотности вероятности ее фигура единичной площади, ограниченной осью x и кривой fη(x), разбивается на произвольное число простых не пересекающихся частей g_j (i=1,k),с площадями P_j (j=1,k), (Рис.8)

Рис.8Разбивка плотности вероятности на отдельном участке

fη(x)

g₁ (Р₁)

g₂ (Р₂) g₃ (Р₃)

x

g₁ (Р₁)

x

Рис. 9 Условные плотности

вероятности

g₂ (Р₂)

x

g₃ (Р₃)

x

Условные плотности вероятности имеют вид (Рис.9)

Для полученных условных плотностей вероятности одним из предыдущих методов определяются случайные последовательности, которые в сумме дадут требуемую случайную последовательность с заданной плотностью вероятности.

5. Оценка закона распределения

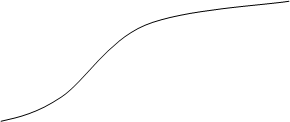
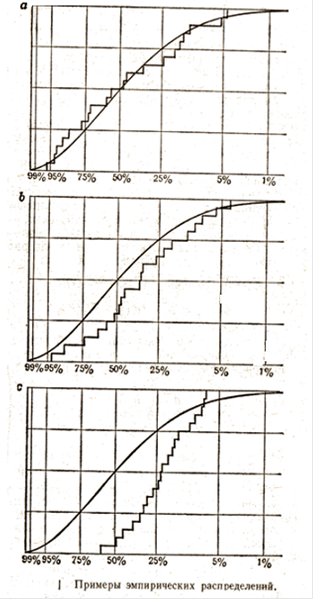
Для полученной случайной последовательности y_1, y_2,…,y_n с заданным законом распределения необходимо провести оценку соответствия заданного закона распределения, который реализует смоделированный датчик случайных чисел. Поэтому для последовательности y_1, y_2,…,y_n строится статистическая функция распределения

F* (y) (Рис. 10). На этом же графике строится интегральная функция распределения F(y) для заданного закона распределения и производится сопоставление F*(y) и F(y). Согласие закона проверяется по критерию Колмогорова. Для этого вычисляется статистика:

Ди=maxF*(y) - F(y) (30)

 

Для конечных решений и распределения статистики Ди получены пороговые значения в форме таблиц (Таблица 1.). По этой таблице для заданных объемов последовательности и и значению статистики Ди определяется уровень значимости  .

Если гипотеза верна то статистика Ди* имеет в пределе при n распределение Колмогорова и квантили уровня P= (1-2) близки к 1. Это значит, что полученный генератор случайных чисел вырабатывает последовательность с заданным законом распределения. Если значения статистики Ди не попадают в пороговые значения, то такой генератор не годится для пользования.

F(y)

F(y) 1

F*(y)

0.5 D_n {

 

y

y₁ y₂  y₃ y₄ …….y_n-1 y_n

 

Рис.10Оценка распределения

III Содержание исследования

Исследование, проводимое в данной работе, заключается в получении программного датчика случайных чисел, пригодного для моделирования случайной последовательности с заданным законом распределения. При этом необходимо разработать алгоритм и программу датчика, а затем исследовать свойства выработанной им последовательности. При проведении исследований необходимо:

1.По двадцати числам (n=20) выведенным на печать построить статистическую функцию распределения F*(y)(рис.10) На этом же графике построить интегральную функцию распределения F(y) для заданного преподавателем закона распределения. Сопоставив значения F*(y)и F(y), вычислить статистику Ди (30).

2. Составить блок- схему и программу для ПЭВМ, в которой следует предусмотреть построение статистического ряда и вычисление статистики Ди по критерию Колмогорова.

3.По таблице пороговых значений статистики Ди произвести оценку распределения.

4. Для полученной последовательности произвести оценку математического ожидания, дисперсии, среднеквадратического отклонения.

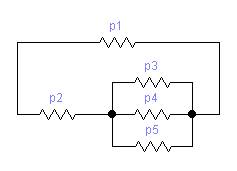
Блок- схема генератора

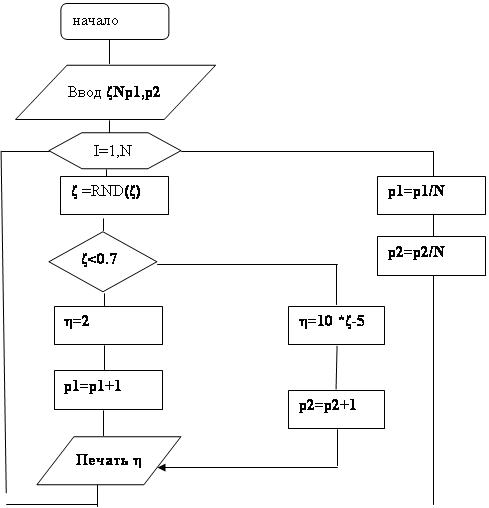Интерфейс программы:

 

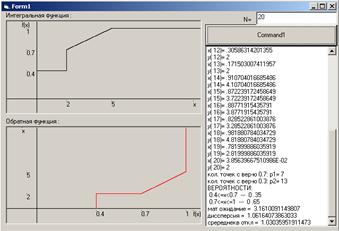
Листинг программы:

 

Private Sub Command1_Click()

Dim n As Integer

Dim p1, p2 As Integer

Dim Y() As Variant, X As Double

p1 = 0: p2 = 0: m = 0: d = 0

List1.Clear

Randomize

X = 0.5

n = Val(Text1.Text)

ReDim Y(n) As Variant

For i = 1 To n

 X = Rnd(X)

 List1.AddItem ("x(" + Str(i) + ")=" + Str(X))

 

 If X < 0.7 Then

p1 = p1 + 1

Y(i) = 2

m = m + Y(i)

List1.AddItem ("y(" + Str(i) + ")=" + Str(Y(i)))

 Else

 p2 = p2 + 1

Y(i) = 10 * X - 5

m = m + Y(i)

List1.AddItem ("y(" + Str(i) + ")=" + Str(Y(i)))

 End If

 

Next i

List1.AddItem ("кол. точек с вер-ю 0.7: p1=" + Str(p1))

List1.AddItem ("кол. точек с вер-ю 0.3: p2=" + Str(p2))

List1.AddItem ("ВЕРОЯТНОСТИ:")

List1.AddItem (" 0.4<=x<0.7 --- 0" + Str(p1 / n))

List1.AddItem (" 0.7<=x<=1 --- 0" + Str(p2 / n))

m = m / n

List1.AddItem ("мат ожидание = " + Str(m))

For i = 1 To n

 d = d + (Y(i) - m) ^ 2

Next i

 d = d / (n - 1)

 b = Sqr(d)

 List1.AddItem ("диссперсия = " + Str(d))

 List1.AddItem ("сререднекв откл = " + Str(b))

'построение интегральной функции

Picture1.Scale (-2, 11)-(11, -2)

Picture1.Line (0, -2)-(0, 11)

Picture1.Line (-2, 0)-(11, 0)

Picture1.PSet (-1, 11)

Picture1.Print ("f(x)")

Picture1.PSet (10.5, -0.3)

Picture1.Print ("x")

Picture1.PSet (-0.7, 4)

Picture1.Print ("0.4")

Picture1.PSet (-0.7, 7)

Picture1.Print ("0.7")

Picture1.PSet (-0.7, 10)

Picture1.Print ("1")

Picture1.PSet (2, -0.3)

Picture1.Print ("2")

Picture1.PSet (5, -0.3)

Picture1.Print ("5")

For i = 0 To 11 Step 0.001

If i < 2 Then

l = 4

Else

If i < 5 Then

l = (0.1 * i + 0.5) * 10

Else

l = 10

End If

End If

Picture1.PSet (i, l)

Next i

Picture1.Line (2, 4)-(2, 7)

'построение обратной функции

Picture2.Scale (-2, 11)-(11, -2)

Picture2.Line (0, -2)-(0, 11)

Picture2.Line (-2, 0)-(11, 0)

Picture2.PSet (-1, 11)

Picture2.Print ("x")

Picture2.PSet (10.5, -0.3)

Picture2.Print ("f(x)")

Picture2.PSet (-0.7, 2)

Picture2.Print ("2")

Picture2.PSet (-0.7, 5)

Picture2.Print ("5")

Picture2.PSet (4, -0.3)

Picture2.Print ("0.4")

Picture2.PSet (7, -0.3)

Picture2.Print ("0.7")

Picture2.PSet (10, -0.3)

Picture2.Print ("1")

For i = 4 To 10 Step 0.001

If i < 7 Then

l = 2

Else

l = i - 5

End If

Picture2.PSet (i, l), vbRed

Next i

Picture2.Line (4, 0)-(4, 2), vbRed

Picture2.Line (10, 5)-(10, 11), vbRed

End Sub