Московский авиационный институт
/государственный университет/
Филиал «Взлет».
Курсовая работа
по Теории вероятности и математической статистике
Выполнил: студент группы
Р 2/1 Костенко В.В.
Проверил: Егорова Т.П.
г.Ахтубинск 2004 г.
Содержание
Задание №1: Проверка теоремы Бернулли на примере моделирования электрической схемы. Распределение дискретной случайной величины по геометрическому закону распределения
Задание №2: Смоделируем случайную величину, имеющую геометрический закон распределения случайной величины
Задание №3: Проверка критерием Колмогорова: имеет ли данный массив соответствующий закон распределения
Список используемой литературы
Задание №1. Проверка теоремы Бернулли на примере моделирования электрической схемы
Определение: При неограниченном увеличении числа опытов n частота события A сходится по вероятности к его вероятности p.
План проверки: Составить электрическую схему из последовательно и параллельно соединенных 5 элементов, рассчитать надежность схемы, если надежность каждого элемента: 0.6 < pi < 0.9. Расчет надежности схемы провести двумя способами. Составить программу в среде Turbo Pascal .
Схема:
Электрическая цепь, используемая для проверки теоремы Бернулли:
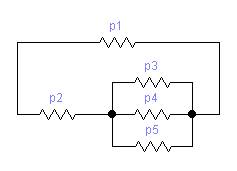
Расчет:
Чтобы доказать выполнимость теоремы Бернулли, необходимо чтобы значение частоты появления события в серии опытов в математическом моделировании равнялось значению вероятности работы цепи при теоретическом расчёте этой вероятности.
Математическое моделирование в среде Turbo Pascal
Program KURSOVIK;
Uses CRT;
Const c=5;
Var op,i,j,n,m:integer;
a,rab,pp,ppp,ppp1,ppp2:real;
p:array[1..c] of real;
x:array[1..c] of byte;
Begin
ClrScr;
Randomize;
p[1]:=0.7; p[2]:=0.8; p[3]:=0.9; p[4]:=0.7; p[5]:=0.8;
Writeln(' Опытов: Исходы: Вероятность:'); Writeln;
For op:=1 to 20 do Begin
n:=op*100;m:=0;
Write(' n=',n:4);
For i:=1 to n do Begin
For j:=1 to c do Begin
x[j]:=0;
a:=random;
if a<p[j] then x[j]:=1;
End;
rab:=x[i]+x[2]*(x[3]+x[4]+x[5]);
If rab>0 then m:=m+1;
End;
pp:=m/n;
writeln(' M= ',m:4,' P*= ',pp:3:3);
End;
ppp1:=p[1]+p[2]*(p[3]+p[4]+p[5]-p[3]*p[4]-p[3]*p[5]-p[4]*p[5]+p[3]*p[4]*p[5]);
ppp2:=p[1]*p[2]*(p[3]+p[4]+p[5]-p[3]*p[4]-p[3]*p[5]-p[4]*p[5]+p[3]*p[4]*p[5]);
ppp:=ppp1-ppp2;
Writeln; Writeln(' Вер. в опыте: p=',ppp:6:3);
Readln;
End.
Результат работы программы
Опытов: Исходы: Вероятность:
n= 100 M= 94 P*= 0.940
n= 200 M= 163 P*= 0.815
n= 300 M= 247 P*= 0.823
n= 400 M= 337 P*= 0.843
n= 500 M= 411 P*= 0.822
n= 600 M= 518 P*= 0.863
n= 700 M= 591 P*= 0.844
n= 800 M= 695 P*= 0.869
n= 900 M= 801 P*= 0.890
n=1000 M= 908 P*= 0.908
n=1100 M= 990 Р*= 0.900
n=1200 M= 1102 P*= 0.918
n=1300 M= 1196 P*= 0.920
n=1400 M= 1303 P*= 0.931
n=1500 M= 1399 P*= 0.933
n=1600 M= 1487 P*= 0.929
n=1700 M= 1576 P*= 0.927
n=1800 M= 1691 P*= 0.939
n=1900 M= 1782 P*= 0.938
n=2000 M= 1877 P*= 0.939
Вероятность в опыте: p= 0.939
Теоретический расчёт вероятности работы цепи:
I способ:

II способ:
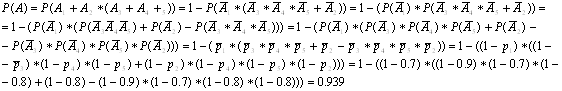
Вывод: Из математического моделирования с помощью Turbo Pascal видно, что частота появления события в серии опытов сходится по вероятности к рассчитанной теоретически вероятности данного события P(A) = 0.939.
Распределение дискретной случайной величины по геометрическому закону распределения
Моделирование случайной величины, имеющей геометрический закон распределения:
(X=xk) = p(1-p)k
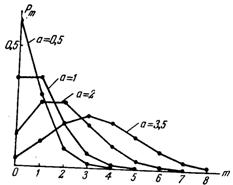
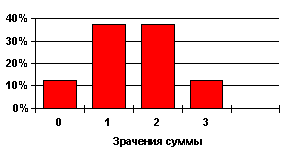
где xk = k=0,1,2…, р – определяющий параметр, 0<p<1. Этот закон является дискретным. Составим теоретический ряд распределения, присваивая р=0,4 и k=0,1,2… и считая Р(Х=xk) получим теоретический многоугольник распределения, изображённый на рис.1.
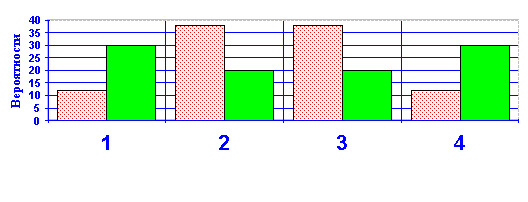
По ряду распределения составим теоретическую функцию распределения F(x), изображённую на рис.2. Смоделируем дискретную случайную величину, имеющую геометрический закон распределения, методом Монте – Карло. Для этого надо:
1. Разбить интервал (0;1) оси ОК на k частичных интервалов:
D1 – (0;р1), D2 – (р1;р1+р2) … Dk – (p1+p2+…+pk-1;1)
2. Разбросать по этим интервалам случайные числа rj из массива, смоделированного датчиком случайных чисел в интервале (0;1). Если rj попало в частичный интервал DI, то разыгрываемая случайная величина приняла возможное значение xi.
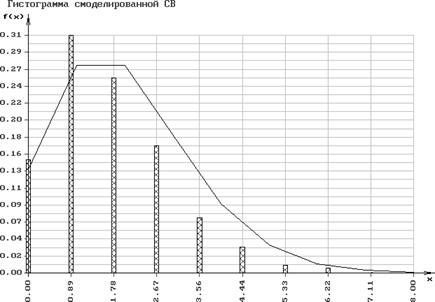
По данным разыгрывания составим статистический ряд распределения Р*(Х) и построим многоугольник распределения, изображенный на рис.1. Построим статистическую функцию распределения F*(X), изображённую на рис.2. Теперь посчитаем теоретические и статистические характеристики дискретной случайной величины, имеющей геометрический закон распределения.

Рис.1.

Рис.2.
Задание №2. Смоделируем случайную величину, имеющую геометрический закон распределения случайной величины
Программа в Turbo Pascal:
Program kursovik;
Uses crt;
Const M=300;
Var
K,I:integer;
P,SI,SII,SP,DTX,DSX,MX,MSX,GT,GS:real;
X:array[1..300] of real;
PI,S,P1,MMX,MS,D,DS,PS,STA,STR:ARRAY[0..10] OF REAL;
BEGIN;
CLRSCR;
randomize;
{ТЕОРЕТИЧЕСКИЙ РЯД}
WRITELN('ТЕОРЕТИЧЕСКИЙ РЯД:');
P:=0.4; SI:=0;
FOR K:=0 TO 10 DO BEGIN
IF K=0 THEN PI[K]:=P ELSE
IF K=1 THEN PI[K]:=P*(1-P) ELSE
IF K=2 THEN PI[K]:=P*SQR(1-P) ELSE
IF K=3 THEN PI[K]:=P*SQR(1-P)*(1-P) ELSE
IF K=4 THEN PI[K]:=P*SQR(SQR(1-P)) ELSE
IF K=5 THEN PI[K]:=P*SQR(SQR(1-P))*(1-P) ELSE
IF K=6 THEN PI[K]:=P*SQR(SQR(1-P))*SQR(1-P) ELSE
IF K=7 THEN PI[K]:=P*SQR(SQR(1-P))*SQR(1-P)*(1-P) ELSE
IF K=8 THEN PI[K]:=P*SQR(SQR(SQR(1-P))) ELSE
IF K=9 THEN PI[K]:=P*SQR(SQR(SQR(1-P)))*(1-P) ELSE
IF K=10 THEN PI[K]:=P*SQR(SQR(SQR(1-P)))*SQR(1-P) ELSE
SI:=SI+PI[K];
WRITELN(' P[',K,']=',PI[K]:6:5);
END;
READLN;
WRITELN('ИНТЕРВАЛЫ:');
P1[1]:=0.4;
FOR K:=1 TO 10 DO BEGIN
P1[K+1]:=PI[K]+P1[K];
WRITELN( 'PI[',K,']=',P1[K]:6:5);
END;
READLN;
{СТАТИСТИЧЕСКИЙ РЯД}
WRITELN;
WRITELN('СТАТИСТИЧЕСКИЙ РЯД:');
FOR I:=1 TO 9 DO BEGIN
X[I]:=RANDOM;
WRITE(X[I]:5:2);
END;
READLN;
FOR I:=10 TO 99 DO BEGIN
X[I]:=RANDOM;
WRITE(X[I]:5:2);
END;
READLN;
FOR I:=100 TO 200 DO BEGIN
X[I]:=RANDOM;
WRITE(X[I]:5:2);
END;
READLN;
FOR I:=201 TO 300 DO BEGIN
X[I]:=RANDOM;
WRITE(X[I]:5:2);
END;
READLN;
PS[K]:=0;
FOR I:=1 TO M DO BEGIN
FOR K:=0 TO 10 DO BEGIN
IF ((X[I]<P1[K]) AND (X[I]>=P1[K-1])) THEN BEGIN
PS[K]:=PS[K]+1;
END;
END;
END;
FOR K:=0 TO 10 DO BEGIN
STA[K]:=PS[K+1]/M;
WRITELN('P*[',K,']=',STA[K]:6:5);
END;
WRITELN;
WRITELN('СТАТИСТИЧЕСКИЕ ИНТЕРВАЛЫ:');
STR[1]:=STA[0];
FOR K:=1 TO 10 DO BEGIN
STR[K+1]:=STR[K]+STA[K];
WRITELN(' PS[',K,']=',STR[K]:6:5);
END;
READLN;
{ТЕОРЕТИЧЕСКОЕ И СТАТИСТИЧЕСКОЕ МАТОЖИДАНИЕ Mx}
MX:=0;
FOR K:=0 TO 10 DO BEGIN
MMX[K]:=K*PI[K];
MX:=MX+MMX[K];
END;
WRITELN('ТЕОРЕТИЧЕСКОЕ МАТОЖИДАНИЕ MX:',MX:6:5);
MSX:=0;
FOR K:=0 TO 10 DO BEGIN
MS[K]:=K*STA[K];
MSX:=MSX+MS[K];
END;
WRITELN('СТАТИСТИЧЕСКОЕ МАТОЖИДАНИЕ Mx*:',MSX:6:5);
WRITELN;
{ТЕОРЕТИЧЕСКАЯ И СТАТИСТИЧЕСКАЯ ДИСПЕРСИЯ Dx}
DTX:=0; DSX:=0;
FOR K:=0 TO 10 DO BEGIN
D[K]:=SQR(K-MX)*PI[K];
DTX:=DTX+D[K];
DS[K]:=SQR(K-MSX)*STA[K];
DSX:=DSX+DS[K];
END;
WRITELN('ТЕОРЕТИЧЕСКАЯ ДИСПЕРСИЯ Dx:',DTX:6:5);
WRITELN('СТАТИСТИЧЕСКАЯ ДИСПЕРСИЯ Dx*:',DSX:6:5);
WRITELN;
{ТЕОР И СТАТ СРЕДНЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ G}
GT:=SQRT(DTX);
GS:=SQRT(DSX);
WRITELN('ТЕОР СРЕДНЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ G:',GT:6:5);
WRITELN('СТАТ СРЕДНЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ G*:',GS:6:5);
WRITELN;
READLN;
END.
Результаты:
ТЕОРЕТИЧЕСКИЙ РЯД:
P[0]=0.40000
P[1]=0.24000
P[2]=0.14400
P[3]=0.08640
P[4]=0.05184
P[5]=0.03110
P[6]=0.01866
P[7]=0.01120
P[8]=0.00672
P[9]=0.00403
P[10]=0.00242
ИНТЕРВАЛЫ:
PI[1]=0.40000
PI[2]=0.64000
PI[3]=0.78400
PI[4]=0.87040
PI[5]=0.92224
PI[6]=0.95334
PI[7]=0.97201
PI[8]=0.98320
PI[9]=0.98992
PI[10]=0.99395
Статистический ряд:
0.57 0.86 0.58 0.11 0.81 0.26 0.17 0.14 0.51 0.53 0.80 0.57 0.17 0.14 0.30 0.58 0.80 0.55 0.86 0.81 0.80 0.18 0.39 0.02 0.74 0.67 0.57 0.32 0.30 0.92 0.64 0.95 0.96 0.25 0.10 0.87 0.44 0.76 0.87 0.43 0.84 0.58 0.62 0.87 0.90 0.70 0.20 0.62 0.08 0.54 0.53 0.47 0.08 0.40 0.30 0.09 0.26 0.54 0.29 0.60 0.95 0.52 0.27 0.99 0.54 0.84 0.75 0.74 0.03 0.42 0.98 0.92 0.32 0.07 0.06 0.49 0.36 0.15 0.03 0.75 0.05 0.17 0.20 0.03 0.54 0.76 0.28 0.16 0.09 0.58 0.96 0.29 0.92 0.88 0.92 0.03 0.57 0.78 0.61 0.05 0.71 0.67 0.10 0.62 0.39 0.10 0.01 0.72 0.27 0.09 0.14 0.60 0.24 0.88 0.40 0.07 0.43 0.39 0.28 0.84 0.68 0.93 0.66 0.65 0.81 0.02 0.02 0.05 0.32 0.29 0.17 0.10 0.34 0.81 0.02 0.26 0.02 0.34 0.23 0.28 0.66 0.43 0.52 0.00 0.16 0.17 0.07 0.11 0.75 0.21 0.37 0.45 1.00 0.29 0.35 0.37 0.54 0.28 0.63 0.25 0.08 0.67 0.30 0.17 0.58 0.93 0.64 0.25 0.68 0.06 0.39 0.35 0.79 0.43 0.80 0.99 0.36 0.64 0.52 0.65 0.29 0.02 0.81 0.01 0.53 0.98 0.89 0.61 0.25 0.32 0.44 0.99 0.14 0.30 0.28 0.44 0.83 0.97 0.01 0.72 0.36 0.09 0.03 0.57 0.21 0.66 0.26 0.80 0.39 0.95 0.48 0.10 0.59 0.39 0.94 0.25
0.28 0.86 0.03 0.98 0.36 0.13 0.80 0.88 0.82 0.64 0.76 0.08 0.28 0.70 0.31 0.49 0.58 0.84 0.60 0.03 0.72 0.04 0.81 0.86 0.84 0.85 0.03 0.87 0.96 0.77 0.28 0.59 0.75 0.38 0.40 0.55 0.57 0.04 0.70 0.70 0.46 0.21 0.79 0.21 0.88 0.70 0.89 0.10 0.35 0.30 0.44 0.25 0.40 0.80 1.00 0.84 0.29 0.16 0.68 0.28 0.48 0.41 0.49 0.17 0.98 0.58 0.53 0.83 0.84 0.70 0.76 0.44 0.40 0.64 0.81 0.89 0.32 0.39 0.21 0.77 0.22 0.05 0.76 0.24
P*[0]=0.44333
P*[1]=0.21000
P*[2]=0.12667
P*[3]=0.11000
P*[4]=0.04000
P*[5]=0.02333
P*[6]=0.01667
P*[7]=0.01000
P*[8]=0.01000
P*[9]=0.00333
P*[10]=0.00148
Статистические интервалы:
PS[1]=0.44333
PS[2]=0.65333
PS[3]=0.78000
PS[4]=0.89000
PS[5]=0.93000
PS[6]=0.95333
PS[7]=0.97000
PS[8]=0.98000
PS[9]=0.99000
PS[10]=0.99333
Числовые характеристики:
MX:1.45465
Mx*:1.36478
Dx:3.29584
Dx*:3.20549
G:1.81544
G*:1.79039
Задание №3. Проверка критерием Колмогорова: имеет ли данный массив соответствующий закон распределения
Воспользуемся критерием Колмогорова. В качестве меры расхождения между теоретическим и статистическим распределениями рассматривается максимальное значение модуля разности между статистической функцией распределения F*(x) и соответствующей теоретической функцией распределения F(x).
D = max | F*(x)- F(x)|
D = 0.04
Далее определяем величину l по формуле:
l = D\| n ,
где n – число независимых наблюдений.
l = D\| n =0,04*\/ 300 = 0,693
и по таблице значений вероятности P(l) находим вероятность P(l).
P(l) = 0,711.
Это есть вероятность того, что (если величина х действительно распределена по закону F(x)) за счёт чисто случайных причин максимальное расхождение между F*(x) и F(x) будет не меньше, чем наблюдаемое.
Нет оснований отвергать гипотезу о том, что наш закон распределения является геометрическим законом распределения.
Воспользуемся критерием Колмогорова. В качестве меры расхождения между теоретическим и статистическим распределениями рассматривается максимальное значение модуля разности между статистической функцией распределения F*(x) и соответствующей теоретической функцией распределения F(x).
D = max | F*(x)- F(x)|
D = 0.04
Далее определяем величину l по формуле:
l = D\| n ,
где n – число независимых наблюдений.
l = D\| n =0,04*\/ 300 = 0,693
и по таблице значений вероятности P(l) находим вероятность P(l).
P(l) = 0,711.
Это есть вероятность того, что (если величина х действительно распределена по закону F(x)) за счёт чисто случайных причин максимальное расхождение между F*(x) и F(x) будет не меньше, чем наблюдаемое.
Нет оснований отвергать гипотезу о том, что наш закон распределения является геометрическим законом распределения.
Список используемой литературы
1. «Теория вероятностей» В. С. Вентцель.
2. «Теория вероятностей (Задачи и Упражнения)» В.С. Вентцель, Л. А. Овчаров.
3. «Справочник по вероятностным расчётам».
4. «Теория вероятностей и математическая статистика» В.Е.Гмурман.
5. «Руководство к решению задач по теории вероятностей и математической статистике» В. Е. Гмурман.
Похожие работы
... вывод, что теорема Бернулли верна. Задание 2,3. Моделирование дискретной случайной величины, имеющей закон распределения Пуассона. Подтверждение гипотезы о том, что полученная случайная величина имеет данный закон распределения с помощью критерия Колмогорова. Закон Пуассона Рассмотрим случайную величину X, которая может принимать целые, неотрицательные значения:0,1,2,... ,m,... Говорят, ...
... гипотезу. Вроде бы это надо делать так: Теперь результаты наблюдений над выручкой G можно представить в виде четырех наблюдений над U: –11,+1,+3,+7. Теория математической статистики предлагает следующий, т.н. биномиальный критерий проверки гипотез в подобных ситуациях. Предполагается, что распределение вероятностей наблюдаемой величины U симметрично относительно значения математического ...
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...





0 комментариев