Пошук у глибину і у ширину

2.2 Пошук у глибину і у ширину

Є дві основні стратегії пошуку потрібної вершини на дереві:

1) пошук у ширину;

2) пошук у глибину (перебір з поверненнями, бектрекінг).

Процедура пошуку у ширину передбачає аналіз на кожному кроці нащадків усіх вершин (паралельна перевірка всіх можливих альтернатив).

Процедура пошуку в глибину передбачає першочерговий аналіз нащадків тих вершин, що були проаналізовані останніми. Всі альтернативи аналізуються послідовно; аналіз деякої альтернативи завершується лише тоді, коли встановлюється, приводить вона до успіху чи ні. Якщо ж альтернатива зумовлює невдачу, відбувається повернення і розгляд інших альтернатив.

На рис.2 показана послідовність перегляду вершин при пошуку в ширину, на рис.3 – пошуку в глибину.

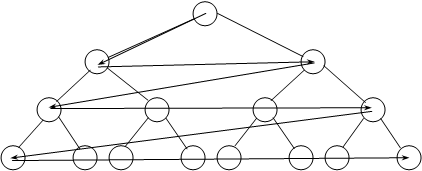
Рис.2. Процедура пошуку в ширину

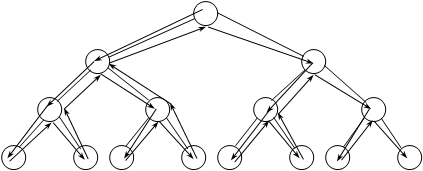
Рис.3. Процедура пошуку в глибину

Пошук в глибину (більш поширений) дозволяє зекономити пам’ять, оскільки при його реалізації не потрібно запам’ятовувати все дерево, а лише вершини, що мають відношення до поточної альтернативи.

2.3. Простір задач і простір станів

При плануванні в просторі станів заданим вважається деякий набір станів (ситуацій). Відомі дії, які може здійснювати система та які визначають перехід з одного стану в інший.

Графом станів задачі називається орієнтований граф, вершини якого відповідають можливим станам предметної області, а дуги – методам переходу від стану до стану.

Дуги можуть мати мітки, які інтерпретуються як вартість або довжина відповідного переходу. Тоді вирішення задачі являє собою пошук шляху від початкового стану до цільового; при цьому типовою вимогою є оптимізація даного рішення (пошуку найкоротшого шляху).

Класичний приклад планування в просторі станів – задача комівояжера.

Планування в просторі задач передбачає декомпозицію початкової задачі на підзадачі, поки не буде досягнути зведення до задач, для яких вже готові алгоритми рішення. Таку декомпозицію можна уявити у вигляді І/АБО графа.

Існують також комбінації планування у просторі задач істанів.

2.4 Автоматний спосіб задання алгоритму

В комп’ютері вхідна послідовність бітів перетворюється у вихідну за допомогою логічних схем. Логічні схеми поділяються на комбінаційні схеми і схеми з пам’яттю (скінченні автомати).

У комбінаційних схемах значення вихідних змінних залежать лише від стану вхідних і не залежать від поточного стану схеми. Будь-яка комбінаційна схема реалізує булеву (0/1) функцію від своїх вхідних змінних.

Скінчений автомат є перетворювачем, вихід якого залежить від входу, але й від поточного стану автомата. При цьому кількість вхідних і вихідних змінних, їх значень є скінченою. Поточний стан автомата – в пам’яті.

Найуніверсальнішою моделлю комп’ютерних обчислень є машина Тьюринга.

Автомати мають пам’ять у вигляді стрічки і пристрій для читання з неї. Стрічка розбита на квадрати з символами. Автомат розглядає символи по черзі, виконує обчислення і розв’язує задачі.

Формально скінчений автомат описується так:

FA=<Q, A, b, q₀, F>

де Q=(q₁, q₂, …, q_n) - скінченна множина станів керування; A=(a₁, a₂, .., a_m) - вхідний алфавіт; b: Q*A→Q - функція переходів; q₀ - початковий стан;  - множина заключних станів керування.

Приклад. Потрібно побудувати скінчений автомат який допускає тільки послідовності 0/1, при цьому в послідовності розпізнавання кількість одиниць повинна бути парною, а нулів – непарною.

Згідно з умовою задачі А складатиметься з символів 0, 1, #, де # позначатиме довільний символ, відмінний від 0 і 1. Тобто, А=<0, 1, #>.

Множину станів виберемо так:

Q=(q₁, q₂, …, q₅),

де q₀ - початковий стан;

q_{1 -} стан помилки;

q₂ - кількість нулів непарна, а одиниць – парна;

q₃ – кількість нулів і одиниць непарна;

q₄ – кількість нулів і одиниць парна;

q₅ – кількість нулів парна, а одиниць – непарна;

Згідно з умовою задачі F=<q₂>

Функції переходів визначаються так:

q0#→q1	q00→q2	q30→q5
q1→q1	q01→q5	q31→q2
q2→q1	q10→q1	q40→q2
q3→q1	q11→q1	q41→q5
q4→q1	q20→q4	q50→q3
q5→q1	q21→q3	q51→q4

Автомати зручно задавати таблично:

	#	0	1	←
q0	q1	q2	q5
q1	q1	q1	q1
q2	q1	q4	q3
q3	q1	q5	q2
q4	q1	q2	q5
q5	q1	q3	q4

Рис.1. Табличне задання автомата

Рядки таблиці позначаються станами множини Q, а стовпці – символами вхідного алфавіту. Символ ← позначає заключні допустимі стани.

Графічний опис автомата полягає у побудові графа, де вершини q_i і q_j з’єднуються дугою a якщо виконується команда q_ia→q_j. Заключні допустимі вершини позначаються подвійним колом.

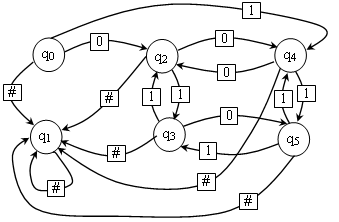
Рис.2. Графічне задання автомата

Спеціальним типом автомата є машина Тьюринга. Універсальна машина Тьюринга може обчислити будь-який інтуїтивний алгоритм.