Способи задання графів

3.2 Способи задання графів

Існує послідовний і зв’язний спосіб задання графів.

Послідовна форма використовує квадратну таблицю (Graf(n,n), n - вершин), яку називають матрицею суміжності. Якщо є зв’язок між вершинами, то Graf(I,j)=1, інакше Graf(I,j)=0.

а) б)

Рис.3. Матриці суміжності графів з рис.2.: а – неорієнтованого, б – орієнтованого

Матриця інцидентності відображає зв’язок n вершин за допомогою m дуг, розмір матриці інцидентності (n*m), але вона менш зручна, ніж матриця суміжності.

Інша форма задання графу – список зв’язності. Граф з n вершинами буде задаватися списками – по одному для кожної вершини. Список для вершини і містить вершини, суміжні з і.

3.3 Дерева

Дерево – це орієнтований ациклічний граф, для якого виконуються такі умови:

1) існує одна вершина, в яка не входить жодне ребро (корінь);

2) у будь-яку вершину, крім кореня, входить лише одне ребро;

3) з кореня можна знайти унікальний шлях до кожної вершини дерева.

Орієнтований граф з кількох вершин – ліс. Бінарне дерево – кожна вершина має два нащадки. При пошуку певного вузла у дереві використовують пряме і зворотне проходження вузлів.

Способи зберігання дерев

Послідовне зберігання ділиться на рівневі і діжкове.

Рівневе: для кожного рівня дерева послідовно вказаються його вузли.

Дужкове: дужками вказуються нащадки даного вузла.

Зв’язне зберігання – списки, кожен список містить вказівними на нащадків.

Пошук у глибину і ширину

Пошук в глибину – послідовно відвідуються всі нові вершини –нащадки (якщо вершина була відвідана, то вона перестає бути новою).

Пошук у ширину – перевіряються суміжні вершини одного рівня, потім – перехід на нижчий рівень.

Остові дерева

Довільне дерево <V, T> неорієнтованого графу G=<V, E> називається остовим.

Ейлерові шляхи

Для вирішення багатьох прикладних проблем використовуються ейлерові шляхи. Ейлеревими називають шляхи, які проходять через кожне ребро графу один раз. Якщо початковий вузол є кінцевим, то такий граф називається ейлеревим циклом.

Задача про Кенігсбергські мости.

Теорема. У графі існує ейлерів шлях тільки тоді, коли граф зв’язний і містить не більше двох вершин непарного ступеня.

Знаходження найкоротших шляхів у графі

Потрібно знайти мінімальний шлях (контур) у навантаженому графі, де d(u,v) - відстань між вершинами u і v, якщо не існує шляху, то d(u,v)=.

4. Загальна схема алгоритму Харта, Нельсона і Рафаеля

Узагальненням алгоритмів пошуку найкоротшого шляху на графах є алгоритм Харта, Нельсона і Рафаеля.

Введемо такі позначення:

s - початкова вершина;

q - цільова вершина;

c(i,j) - довжина ребра між вершинами і та j;

d(i, j) - довжина найкоротшого шляху між і-ю та j-ю вершинами;

g(n) - довжина найкоротшого шляху між від початкової вершини до n-ї;

h(n) - довжина найкоротшого шляху між від n-ї вершини до цільової;

f(n) - довжина найкоротшого шляху між від початкової вершини до цільової, які проходять через вершину n, при цьому f(n)=g(n)+h(n);

g*(n) – оцінка довжини найкоротшого шляху між від початкової вершини до n-ї;

h*(n) – евристична функція, яка задає оцінку довжини найкоротшого шляху між від n-ї вершини до цільової;

f*(n)=g*(n)+h*(n) - оцінка f(n);

L(n) - множина всіх наступників вершини n.

Введемо робочі множини: OPEN I CLOSE.

Загальна схема пошуку найкоротшого шляху:

1.         Сформувати шраф пошуку G, який спочатку складається з початкової вершини s. Занести s до OPEN. Прокласти g*(s)=g(s)=0.

2.         Сформувати множину CLOSE, яка спочатку буде порожня.

3.         Якщо множина OPEN порожня, то вихід – потрібного шляху не існує;

4.         Взяти з множини OPEN перший елемент m (відповідно до порядку, встановленого кроком 9), вилучити m з OPEN та занести її до CLOSE.

5.         Якщо m - цільова вершина, то успіх. Відновити шлях від s до m на основі відновлюючи вказівників, що встановлені на кроках 6-8 і завершити алгоритм.

6.         Розкрити вершину m, отримати множину наступників L(m). Додати до графу G всі вершини, які належать L(m), але не належать G, разом з відповідними дугами. Додати ці вершини до OPEN. Для кожної вершини  обчислити оцінки f*(k)=g*(k)+h*(k), поклавши g*(k)=g*(m)+c(m,k), встановити з k до m відновлюючий вказівник;

7.         Для кожної вершини n з тих, які потрапили до L(m), але вже належали OPEN або CLOSE, переобчислити оцінки g*(n)=min((g*(m)+c(m,n), g*(n)). Якщо оцінка зменшилася, то перевстановити з неї відновлюючий вказівник до m.

8.         Для всіх вершин з L(m), які до цього знаходилися в CLOSE, перевстановити відновлюючи вказівними для кожного з наступників цих вершин у напрямі найкоротшого шляху.

9.         Перевпорядкувати множину OPEN за зростанням значень f*.

10.      Повернутися на крок 3.

Якщо евристична функція не використовується, тобто h*(n)=0 і f*(n)=g*(n), то отримується алгоритм Дейкстри.

Якщо взяти g*(n)=0, утворюється алгоритм Дорана і Мічі.

4.1 Планування в просторі задач. І-АБО граф

Планування в просторі задач полягає в розбитті задачі на підзадачі, поки під задача не зведеться до елементарної (для якої існує готовий алгоритм розв’язку).

Для планування в просторі задач втрадиційно використовують І-АБО графи.

І-АБО графом називають орієнтований граф, вершини якого відповідають задачам, а дуги – відношенням між задачами (І - АБО).

І-АБО графи фактично є фрагментами мереж виведення продукційних систем. Розглянемо продукцій ну систему

A → C

B → C

D, C → G

Для такої системи існує І-АБО граф

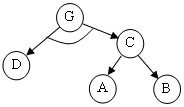
Рис.15.1. І-АБО граф

Вершина C пов’язана з вершинами A i B відношенням АБО (достатньо виконання однієї підзадачі), а вершина G пов’язана з вершинами D i C відношенням І (необхідне виконання всіх підзадач).

4.2 Метод „Поділяй і пануй”

Нехай потрібно вирішити задачу для елементів масиву початкових даних від p до q.

Метод „поділяй і пануй”, або поділ на підзадачі, можна записати у вигляді рекурсивної процедури SubTask.

Булeва функція Small(p, q) визначає, чи не зведена під задача до елементарної. Якщо задача елементарна, то знаходиться її розв’язок за допомогою функції G(p,q).

Якщо задача не елементарна, то вона ділиться на дві частини функцією Divide(p,q). Процедура Combine рекурсивно викликає на виконання процедуру SubTask, але для меншої розмірності вхідних даних. Процес рекурсивно продовжується до тих пір, поки всі задачі не будуть зведені до елементарних.

procedure SubTask(p, q:integer);

Var m:integer;

Begin

if Small(p, q) then G(p,q);

else

begin

m:=Divide(p,q); { p <= m < q }

Combine (SubTask(p,m), SubTask(m+1,q));

end;

End;