Навигация
Нелинейное программирование
Южно-Уральский Государственный Университет
Кафедра АиУ
реферат на тему:
Нелинейное программирование
Выполнил: Пушников А. А., ПС-263.
Проверил: Разнополов О.А.
Челябинск – 2003.
Оглавление
1. Постановка задачи нелинейного программирования
2. Критерии оптимальности в задачах с ограничениями
2.1. Задачи с ограничением в виде равенств
2.2. Множители Лагранжа
3. Условия Куна-Таккера
3.1. Условия Куна-Таккера и задача Куна-Таккера
3.2. Интерпретация условий Куна-Таккера
3.3. Теоремы Куна-Таккера
4. Функции нескольких переменных
4.1. Методы прямого поиска
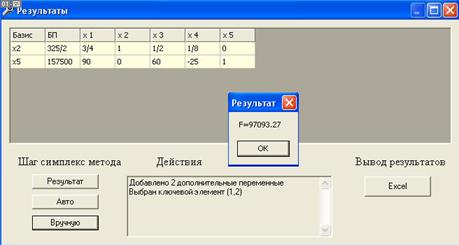
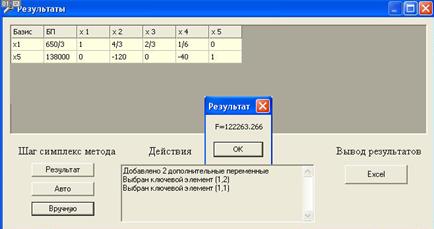
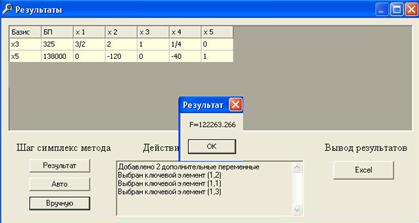
4.1.1. Метод поиска по симплексу (S2 - метод)
4.1.2. Метод поиска Хука-Дживса
1. Постановка задачи нелинейного программирования.
В задаче нелинейного программирования (НЛП) требуется найти значение многомерной переменной х=(![]() ), минимизирующее целевую функцию f(x) при условиях, когда на переменную х наложены ограничения типа неравенств
), минимизирующее целевую функцию f(x) при условиях, когда на переменную х наложены ограничения типа неравенств
![]() , i=1,2,…,m (1)
, i=1,2,…,m (1)
а переменные ![]() , т.е. компоненты вектора х, неотрицательны:
, т.е. компоненты вектора х, неотрицательны:
![]()
![]() (2)
(2)
Иногда в формулировке задачи ограничения (1) имеют противоположные знаки неравенств. Учитывая, однако, что если ![]() , то
, то ![]() , всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например
, всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например ![]() , то их можно представить в виде пары неравенств
, то их можно представить в виде пары неравенств ![]() ,
, ![]() , сохранив тем самым типовую формулировку задачи.
, сохранив тем самым типовую формулировку задачи.
2. Критерии оптимальности в задачах с ограничениями.
Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой проводится поиск оптимума. На первый взгляд может показаться, что уменьшение размеров допустимой области должно упростить процедуру поиска оптимума. Между тем, напротив, процесс оптимизации становится более сложным, поскольку установленные выше критерии оптимальности нельзя использовать при наличии ограничений. При этом может нарушаться даже основное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым градиентом. Например, безусловный минимум функции ![]() имеет место в стационарной точке х=2. Но если задача минимизации решается с учетом ограничения
имеет место в стационарной точке х=2. Но если задача минимизации решается с учетом ограничения ![]() , то будет найден условный минимум, которому соответствует точка x=4. Эта точка не является стационарной точкой функции f, так как
, то будет найден условный минимум, которому соответствует точка x=4. Эта точка не является стационарной точкой функции f, так как ![]() (4)=4. Далее исследуются необходимые и достаточные условия оптимальности решений задач с ограничениями. Изложение начинается с рассмотрения задач оптимизации, которые содержат только ограничения в виде равенств.
(4)=4. Далее исследуются необходимые и достаточные условия оптимальности решений задач с ограничениями. Изложение начинается с рассмотрения задач оптимизации, которые содержат только ограничения в виде равенств.
Рассмотрим общую задачу оптимизации, содержащую несколько ограничений в виде равенств:
Минимизировать ![]()
при ограничениях ![]() , k=1,…,n
, k=1,…,n
Эта задача в принципе может быть решена как задача безусловной оптимизации, полученная путем исключения из целевой функции k независимых переменных с помощью заданных равенств. Наличие ограничений в виде равенств фактически позволяет уменьшить размерность исходной задачи с n до n-k.. В качестве иллюстрации рассмотрим следующий пример.
Пример 1
Минимизировать
![]()
при ограничении ![]()
Исключив переменную ![]() , с помощью уравнения
, с помощью уравнения ![]() , получим
, получим
оптимизационную задачу с двумя переменными без ограничений
min ![]()
Метод исключения переменных применим лишь в тех случаях, когда уравнения, представляющие ограничения, можно разрешить относительно некоторого конкретного набора независимых переменных. При наличии большого числа ограничений в виде равенств, процесс исключения переменных становится весьма трудоемкой процедурой. Кроме того, возможны ситуации, когда уравнение не удается разрешить относительно переменной. В частности, если в примере 1 ограничение ![]() задать в виде
задать в виде
![]()
то получить аналитическое выражение какой-либо из переменных через другие не представляется возможным. Таким образом, при решении задач, содержащих сложные ограничения в виде равенств, целесообразно использовать метод множителей Лагранжа, описание которого дается в следующем разделе.
2.2. Множители ЛагранжаС помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде равенств. При этом задача с ограничениями преобразуется в эквивалентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Лагранжа.
Рассмотрим задачу минимизации функции n переменных с учетом одного ограничения в виде равенства:
Минимизировать
![]() (3)
(3)
при ограничениях ![]() (4)
(4)
В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной оптимизации:
минимизировать L(x,u)=f(x)-u*h(x) (5)
Функция L(х;u) называется функцией Лагранжа, u — неизвестная постоянная, которая носит название множителя Лагранжа. На знак u никаких требований не накладывается.
Пусть при заданном значении u=u0 безусловный минимум функции L(x,u) по х достигается в точке ![]() и
и ![]() удовлетворяет уравнению
удовлетворяет уравнению ![]() . Тогда, как нетрудно видеть, x0 минимизирует (1) с учетом (4), поскольку для всех значений х, удовлетворяющих (4),
. Тогда, как нетрудно видеть, x0 минимизирует (1) с учетом (4), поскольку для всех значений х, удовлетворяющих (4), ![]() и L(x,u)=min f(x).
и L(x,u)=min f(x).
Разумеется, необходимо подобрать значение u=u° таким образом, чтобы координата точки безусловного минимума х° удовлетворяла равенству (4). Это можно сделать, если, рассматривая u как переменную, найти безусловный минимум функции (5) в виде функции u, а затем выбрать значение u, при котором выполняется равенство (4). Проиллюстрируем это на конкретном примере.
Пример 2
Минимизировать
![]()
при ограничении ![]() =0
=0
Соответствующая задача безусловной оптимизации записывается в следующем виде:
минимизировать
L(x,u)= ![]() -u
-u![]()
Решение. Приравняв две компоненты градиента L к нулю, получим
![]()
![]()
Для того чтобы проверить, соответствует ли стационарная точка х° минимуму, вычислим элементы матрицы Гессе функции L(х;u), рассматриваемой как функция х,
![]() ,
,
которая оказывается положительно определенной. Это означает, что L(х,,u) — выпуклая функция х. Следовательно, координаты ![]() ,
,![]() определяют точку глобального минимума. Оптимальное значение u находится путем подстановки значений
определяют точку глобального минимума. Оптимальное значение u находится путем подстановки значений ![]() и
и ![]() в уравнение
в уравнение ![]() =2, откуда 2u+u/2=2 или
=2, откуда 2u+u/2=2 или ![]() . Таким образом, условный минимум достигается при
. Таким образом, условный минимум достигается при ![]() и
и ![]()
![]() и равен min f(x)=4/5.
и равен min f(x)=4/5.
При решении задачи из примера 2 мы рассматривали L(х;u) как функцию двух переменных ![]() и
и ![]() и, кроме того, предполагали, что значение параметра u выбрано так, чтобы выполнялось ограничение. Если же решение системы
и, кроме того, предполагали, что значение параметра u выбрано так, чтобы выполнялось ограничение. Если же решение системы
![]() , j=1,2,3,…,n
, j=1,2,3,…,n
в виде явных функций u получить нельзя, то значения х и u находятся путем решения следующей системы, состоящей из n+1 уравнений с n+1 неизвестными:
![]() , j=1,2,3,…,n
, j=1,2,3,…,n ![]()
Для нахождения всех возможных решений данной системы можно использовать численные методы поиска (например, метод Ньютона). Для каждого из решений (![]() ) следует вычислить элементы матрицы Гессе функции L, рассматриваемой как функция х, и выяснить, является ли эта матрица положительно определенной (локальный минимум) или отрицательно определенной (локальный максимум).
) следует вычислить элементы матрицы Гессе функции L, рассматриваемой как функция х, и выяснить, является ли эта матрица положительно определенной (локальный минимум) или отрицательно определенной (локальный максимум).
Метод множителей Лагранжа можно распространить на случай, когда задача имеет несколько ограничений в виде равенств. Рассмотрим общую задачу, в которой требуется
Минимизировать f(x)
при ограничениях ![]() =0, k=1, 2, ..., К.
=0, k=1, 2, ..., К.
Функция Лагранжа принимает следующий вид:
L(x,u)=f(x)-![]()
Здесь ![]() —множители Лагранжа, т.е. неизвестные параметры, значения которых необходимо определить. Приравнивая частные производные L по х к нулю, получаем следующую систему n уравнении с n неизвестными:
—множители Лагранжа, т.е. неизвестные параметры, значения которых необходимо определить. Приравнивая частные производные L по х к нулю, получаем следующую систему n уравнении с n неизвестными:
![]()
![]()
………..
![]()
Если найти решение приведенной выше системы в виде функций вектора u оказывается затруднительным, то можно расширить систему путем включения в нее ограничений в виде равенств
![]()
![]()
![]()
Решение расширенной системы, состоящей из n+К уравнений с n+К неизвестными, определяет стационарную точку функции L. Затем реализуется процедура проверки на минимум или максимум, которая проводится на основе вычисления элементов матрицы Гессе функции L, рассматриваемой как функция х, подобно тому, как это было проделано в случае задачи с одним ограничением. Для некоторых задач расширенная система n+К уравнений с n+K неизвестными может не иметь решений, и метод множителей Лагранжа оказывается неприменимым. Следует, однако, отметить, что такие задачи на практике встречаются достаточно редко.
3. Условия Куна-Таккера
В предыдущем разделе было установлено, что множители Лагранжа можно использовать при построении критериев оптимальности для задач оптимизации с ограничениями в виде равенств. Кун и Таккер обобщили этот подход на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств.
Рассмотрим следующую общую задачу нелинейного программирования:
минимизировать ![]() (0)
(0)
при ограничениях ![]() (1)
(1)
![]() (2)
(2)
Определение:
Ограничение в виде неравенства ![]() называется активным, или связывающим, в точке
называется активным, или связывающим, в точке ![]() , если
, если ![]() , и неактивным, или несвязывающим, если
, и неактивным, или несвязывающим, если ![]()
Если существует возможность обнаружить ограничения, которые неактивны в точке оптимума, до непосредственного решения задачи, то эти ограничения можно исключить из модели и тем самым уменьшить ее размеры. Основная трудность заключается при этом в идентификации неактивных ограничений, предшествующей решению задачи.
Кун и Таккер построили необходимые и достаточные условия оптимальности для задач нелинейного программирования, исходя из предположения о дифференцируемости функций ![]() . Эти условия оптимальности, широко известные как условия Куна—Таккера, можно сформулировать в виде задачи нахождения решения некоторой системы нелинейных уравнений и неравенств, или, как иногда говорят, задачи Куна—Таккера.
. Эти условия оптимальности, широко известные как условия Куна—Таккера, можно сформулировать в виде задачи нахождения решения некоторой системы нелинейных уравнений и неравенств, или, как иногда говорят, задачи Куна—Таккера.
Найти векторы ![]() ,удовлетворяющие следующим условиям
,удовлетворяющие следующим условиям
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Прежде всего проиллюстрируем условия Куна — Таккера на примере.
Пример 3
Минимизировать ![]()
при ограничениях ![]()
Решение.
Записав данную задачу в виде задачи нелинейного программирования (0)-(2), получим
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Уравнение (3), входящее в состав условий Куна—Таккера, принимает следующий вид:
![]()
откуда
![]()
Неравенства (4) и уравнения (5) задачи Куна — Таккера в данном случае записываются в виде
![]()
![]()
![]()
Уравнения (5.16), известные как условие дополняющей нежесткости, принимают вид
![]()
![]()
Заметим, что на переменные ![]() и
и ![]() накладывается требование неотрицательности, тогда как ограничение на знак
накладывается требование неотрицательности, тогда как ограничение на знак ![]() отсутствует.
отсутствует.
Таким образом, этой задачи условия Куна—Танкера записываются в следующем виде:
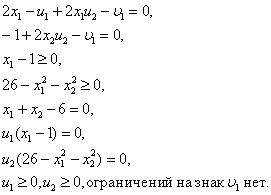
Для того чтобы интерпретировать условия Куна — Таккера, рассмотрим задачу нелинейного программирования с ограничениями в виде равенств:
минимизировать ![]()
при ограничениях ![]()
Запишем условия Куна—Таккера
![]() (8)
(8)
![]() (9)
(9)
Далее рассмотрим функцию Лагранжа для задачи нелинейного программирования с ограничениями в виде равенств
![]()
Для этой функции условия оптимальности первого порядка записываются в виде
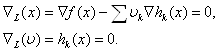
Нетрудно видеть, что условия Куна-Таккера (8) и (9) совпадают с условиями оптимальности первого порядка для задачи Лагранжа.
Рассмотрим задачу нелинейного программирования с ограничениями в виде неравенств:
минимизировать ![]()
при ограничениях ![]()
![]()
Запишем условия Куна—Таккера

Соответствующая функция Лагранжа имеет вид
![]()
Условия оптимальности первого порядка записываются как

Заметим, что ![]() - множитель Лагранжа, соответствующий ограничению
- множитель Лагранжа, соответствующий ограничению ![]() . Раньше было показано, что
. Раньше было показано, что ![]() представляет неявную цену, ассоциированную с ограничением
представляет неявную цену, ассоциированную с ограничением ![]() ; другими словами, величина
; другими словами, величина ![]() отражает изменение минимального значения целевой функции
отражает изменение минимального значения целевой функции ![]() , вызываемое единичным приращением правой части
, вызываемое единичным приращением правой части ![]() - го ограничения.
- го ограничения.
Если предположить, что ![]() - е ограничение является неактивным (т.е.
- е ограничение является неактивным (т.е. ![]() С другой стороны, если
С другой стороны, если ![]() -е ограничение активное (т. е.
-е ограничение активное (т. е. ![]() ), то соответствующая неявная цена
), то соответствующая неявная цена ![]() не обязательно равна нулю, однако
не обязательно равна нулю, однако ![]() , так как
, так как ![]() . Таким образом,
. Таким образом,![]() для всех значений
для всех значений ![]() .
.
Для того чтобы определить знак ![]() (неявной цены, ассоциированной с ограничением
(неявной цены, ассоциированной с ограничением ![]() ), следует увеличить правую часть ограничения от 0 до 1. Ясно, что при этом область допустимых решений сужается, поскольку любое решение, удовлетворяющее ограничению
), следует увеличить правую часть ограничения от 0 до 1. Ясно, что при этом область допустимых решений сужается, поскольку любое решение, удовлетворяющее ограничению ![]() , автоматически удовлетворяет неравенству
, автоматически удовлетворяет неравенству ![]() . Следовательно, размеры допустимой области уменьшаются, и минимальное значение
. Следовательно, размеры допустимой области уменьшаются, и минимальное значение ![]() улучшить невозможно (так как вообще оно может только возрастать). Другими словами, неявная цена
улучшить невозможно (так как вообще оно может только возрастать). Другими словами, неявная цена ![]() , ассоциированная с
, ассоциированная с ![]() -м ограничением, должна быть неотрицательной, что соответствует условиям Куна—Таккера.
-м ограничением, должна быть неотрицательной, что соответствует условиям Куна—Таккера.
В предыдущем разделе построены условия Куна—Таккера для задач условной оптимизации. С помощью метода множителей Лагранжа получено интуитивное представление о том, что условия Куна — Танкера тесно связаны с необходимыми условиями оптимальности. В данном разделе рассматриваются строгие формулировки необходимых и достаточных условий оптимальности решения задачи нелинейного программирования.
Теорема 1. Необходимость условий Куна—Таккера
Рассмотрим задачу нелинейного программирования (0)-(2). Пусть ![]() -
дифференцируемые функции, а х* — допустимое решение данной задачи. Положим
-
дифференцируемые функции, а х* — допустимое решение данной задачи. Положим ![]() . Далее пусть
. Далее пусть ![]() линейно независимы. Если х* — оптимальное решение задачи нелинейного программирования, то существует такая пара векторов
линейно независимы. Если х* — оптимальное решение задачи нелинейного программирования, то существует такая пара векторов ![]() , что
, что![]() является решением задачи Куна—Таккера (3)—(7).
является решением задачи Куна—Таккера (3)—(7).
Условие, согласно которому ![]() должны быть линейно независимыми, известно как условие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое почти всегда выполняется для встречающихся на практике задач оптимизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свойствами.
должны быть линейно независимыми, известно как условие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое почти всегда выполняется для встречающихся на практике задач оптимизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свойствами.
Похожие работы
... гиперповерхность наивысшего (наименьшего) уровня: f (x1, x2, …, xn) = h. Указанная точка может находиться как на границе области допустимых решений, так и внутри неё. Процесс нахождения решения задачи нелинейного программирования с использованием ее геометрической интерпретации включает следующие этапы: 1. Находят область допустимых решений задачи, определяемую соотношениями (если она пуста, ...
... все многообразие факторов, имеющих место в реальных системах, т. е. использованию моделей, более адекватных исследуемым явлениям. Библиографический список 1 Лященко И.Н. Линейное и нелинейное программирования / И.Н.Лященко, Е.А.Карагодова, Н.В.Черникова, Н.З.Шор. – К.: «Высшая школа», 1975, 372 с. 2 Методические указания для выполнения курсового проекта по дисциплине «Прикладная ...
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
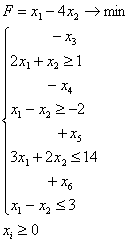
0 комментариев