Навигация
Операционная среда моделирования
4. Операционная среда моделирования
Windows XP – новая операционная система фирмы Microsoft, непосредственно преемница Windows 2000. В основном повторяя архитектуру своей предшественницы, она делает свою работу на компьютере более эффективно и предоставляет пользователю много дополнительных возможностей, кроме того появился новый интерфейс
Основные задачи, связанные с работой в среде Windows 98:
· Загрузка Windows XP и завершение работы на компьютере
· Получение помощи по ходу работы
· Выбор типа пользовательского интерфейса
· Использование стандартных панелей
· Смена языка
· Управление загрузкой Windows XP
Обладая вытесняющей многозадачностью, способностью исполнять несколько программ одновременно и перераспределять ресурсы компьютера между ними по собственной инициативе.
Имеет высокий уровень совместимости с ранее накопленном программным обеспечением, которое разрабатывалось для MS-DOS и предыдущих версий Windows
Требования Windows XP к компьютеру:
· Микропроцессор работающий с тактовой частотой 400МГц (Pentium, Pentium Pro, Pentium 3,4)
· Мышью Microsoft Mouse или другими, подобными по функциям устройствам
· Оперативная память не менее 64 Мбайт
5. Контрольная задача
Пример:
1. Требуется найти минимум функции
![]() , где
, где ![]()
2. Интервал поиска
![]()
![]()
3. Начальная точка: ![]()
4. Параметры поиска: коэффициент шага ![]() число попыток в каждой точке
число попыток в каждой точке ![]()
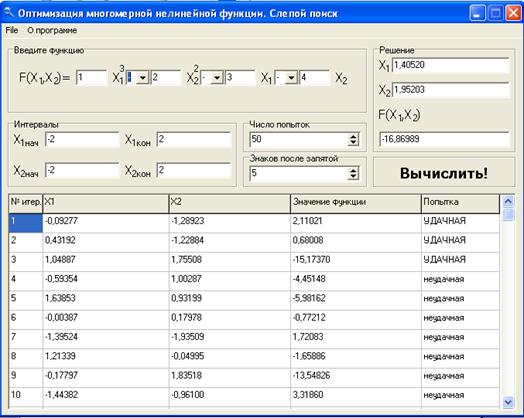
Результаты вычислений представлены в таблице 1.
| Номер итерации | Х | Х | F | Попытка |
| 1 | -0.4282 | -0.8868 | 7.3722 | УДАЧНО |
| 2 | -0.3375 | -0.9057 | 7.3722 | Неудачно |
| 3 | -0.3375 | -0.7358 | 7.3722 | Неудачно |
| 4 | -0.2469 | -0.7358 | 7.3722 | Неудачно |
| 5 | -0.2166 | -0.5660 | 7.3722 | Неудачно |
| 6 | -0.1965 | -0.3962 | 7.3722 | Неудачно |
| 7 | -0.1159 | -0.3019 | 7.3722 | Неудачно |
| 8 | -0.1864 | -0.1887 | 1.7359 | УДАЧНО |
| 9 | -0.2771 | -0.1132 | 1.7359 | Неудачно |
| 10 | -0.1864 | -0.1509 | 1.2884 | УДАЧНО |
| 11 | -0.0957 | -0.1887 | 1.2884 | Неудачно |
| 12 | -0.0353 | -0.0566 | 1.2884 | Неудачно |
| 13 | -0.0856 | 0.0943 | 1.2884 | Неудачно |
| 14 | -0.0151 | 0.2075 | 1.2884 | Неудачно |
| 15 | 0.8514 | 0.9623 | -3.8412 | УДАЧНО |
| 16 | 0.9421 | 0.9057 | -3.8412 | Неудачно |
| 17 | 0.9824 | 1.0755 | -3.9723 | УДАЧНО |
Последнюю точку (17) можно считать решением, так как за заданное число попыток (17), не удалось найти лучшую точку. Возможно увеличив число таких попыток, можно найти лучшее решение. Вывод можно сделать такой: данная программа удачно справляется с возложенными на неё задачами
Заключение
Данная программа может быть использована в качестве наглядного пособия для изучения оптимизации многомерной нелинейной функции методом слепого поиска. Обеспечивает корректную работу и вывод результатов.
Программа также может применяться для оптимального проектирования (выбор наилучших технологических режимов, структуры технологических цепочек, условий экономической деятельности), оптимального управления, построение нелинейных математических модулей, объектов управления (минимизации различных структуры модели и реального объекта).
Недостатком данной программы является отсутствие графического представления моделирования, однако для его осуществления, необходимо ограничивать диапазона выбираемого для подсчёта интервала, что напрямую сказывается на полезность программы.
Список используемой литературы
1. Ю.В. Васильков, Н.Н. Василькова «Компьютерные технологии вычислений в математическом моделировании»
2. Род Стивенс «Delphi. Готовые алгоритмы», М., 2004
3. А.Я. Архангельский «Delphi 7. Справочное пособие», М., 2004
4. А.Я. Архангельский «Программирование в Delphi 7», М., 2004
Приложение
Листинг программы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Spin, Grids, Buttons, Menus;
type
TForm1 = class(TForm)
GroupBox1: TGroupBox;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
ComboBox1: TComboBox;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
ComboBox2: TComboBox;
Label10: TLabel;
Label11: TLabel;
ComboBox3: TComboBox;
Label12: TLabel;
Label13: TLabel;
GroupBox2: TGroupBox;
Label14: TLabel;
Label15: TLabel;
Label16: TLabel;
Label17: TLabel;
Label18: TLabel;
Label19: TLabel;
Label20: TLabel;
Label21: TLabel;
GroupBox3: TGroupBox;
SpinEdit9: TSpinEdit;
StringGrid1: TStringGrid;
GroupBox4: TGroupBox;
Label22: TLabel;
Label23: TLabel;
Label24: TLabel;
Label25: TLabel;
GroupBox5: TGroupBox;
SpinEdit10: TSpinEdit;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Edit5: TEdit;
Edit6: TEdit;
Edit7: TEdit;
Edit8: TEdit;
Edit9: TEdit;
Edit10: TEdit;
Edit11: TEdit;
MainMenu1: TMainMenu;
File1: TMenuItem;
Close1: TMenuItem;
N1: TMenuItem;
Label26: TLabel;
GroupBox6: TGroupBox;
SpeedButton1: TSpeedButton;
procedure FormCreate (Sender: TObject);
procedure SpeedButton1Click (Sender: TObject);
procedure Close1Click (Sender: TObject);
procedure N1Click (Sender: TObject);
private
{Private declarations}
public
{Public declarations}
end;
var
Form1: TForm1;
implementation
uses Math, Unit2;
{$R *.dfm}
procedure TForm1. FormCreate (Sender: TObject);
begin
// задаём названия заголовков грайда
StringGrid1. Cols[0].Text:='№ итер.';
StringGrid1. Cols[1].Text:='X1';
StringGrid1. Cols[2].Text:='X2';
StringGrid1. Cols[3].Text:='Значение функции';
StringGrid1. Cols[4].Text:='Попытка';
end;
procedure TForm1. SpeedButton1Click (Sender: TObject);
var I: Integer;
A, B, C, D, x11, x12, x21, x22, x1, x2, x1opt, x2opt, y, Yopt:real;
begin
// присваиваем для удобства значения переменных
A:=StrToFloat (Edit1. Text);
B:=StrToFloat (Edit2. Text);
C:=StrToFloat (Edit3. Text);
D:=StrToFloat (Edit4. Text);
x11:=StrToFloat (Edit5. Text);
x12:=StrToFloat (Edit6. Text);
x21:=StrToFloat (Edit7. Text);
x22:=StrToFloat (Edit8. Text);
// создаем в грайде строки
StringGrid1. RowCount:=SpinEdit9. Value+1;
for I:=1 to SpinEdit9. Value do
BEGIN
// получение случайных значений координат точки
{**************************************}
randomize;
x1:= (x12 – x11) *random+ x11;
x2:= (x22 – x21) *random+ x21;
{**************************************}
// вычисляем значение функции
if (ComboBox1. Text='-') and (ComboBox2. Text='-') and (ComboBox3. Text='-')
then
y:=A*(x1*x1*x1) – B*(x2*x2) – C*x1 – D*x2;
if (ComboBox1. Text='-') and (ComboBox2. Text='-') and (ComboBox3. Text='+')
then
y:=A*(x1*x1*x1) – B*(x2*x2) – C*x1 + D*x2;
if (ComboBox1. Text='-') and (ComboBox2. Text='+') and (ComboBox3. Text='-')
then
y:=A*(x1*x1*x1) – B*(x2*x2) + C*x1 – D*x2;
if (ComboBox1. Text='+') and (ComboBox2. Text='-') and (ComboBox3. Text='-')
then
y:=A*(x1*x1*x1) + B*(x2*x2) – C*x1 – D*x2;
if (ComboBox1. Text='+') and (ComboBox2. Text='+') and (ComboBox3. Text='-')
then
y:=A*(x1*x1*x1) + B*(x2*x2) + C*x1 – D*x2;
if (ComboBox1. Text='-') and (ComboBox2. Text='+') and (ComboBox3. Text='+')
then
y:=A*(x1*x1*x1) – B*(x2*x2) + C*x1 + D*x2;
if (ComboBox1. Text='+') and (ComboBox2. Text='+') and (ComboBox3. Text='+')
then
y:=A*(x1*x1*x1) + B*(x2*x2) + C*x1 + D*x2;
if (ComboBox1. Text='+') and (ComboBox2. Text='-') and (ComboBox3. Text='+')
then
y:=A*(x1*x1*x1) + B*(x2*x2) – C*x1 + D*x2;
// проверка номера итерации
if i=1 then
begin
x1opt:=x1;
x2opt:=x2;
Yopt:=y;
end
else
begin
if Yopt>y then
// выбираем следуещее более оптимальное значение
begin
x1opt:=x1;
x2opt:=x2;
Yopt:=y;
StringGrid1. Cells [4, i]:='УДАЧНАЯ';
end
else StringGrid1. Cells [4, i]:='неудачная';
end;
// добавляем данные в грайд
StringGrid1. Cells [0, i]:=inttostr(i);
StringGrid1. Cells [1, i]:=FloatToStrF (x1, ffFixed, 15, SpinEdit10. Value);
StringGrid1. Cells [2, i]:=FloatToStrF (x2, ffFixed, 15, SpinEdit10. Value);
StringGrid1. Cells [3, i]:=FloatToStrF (y, ffFixed, 15, SpinEdit10. Value);
END;
Edit9. Text:=FloatToStrF (x1opt, ffFixed, 15, SpinEdit10. Value);
Edit10. Text:=FloatToStrF (x2opt, ffFixed, 15, SpinEdit10. Value);
Edit11. Text:=FloatToStrF (Yopt, ffFixed, 15, SpinEdit10. Value);
end;
procedure TForm1. Close1Click (Sender: TObject);
begin
close;
end;
procedure TForm1.N1Click (Sender: TObject);
begin
Beep;
// показываем модально какое-нибудь окно о проге
form2. ShowModal;
end;
end.
Похожие работы
... философии - особенно с методологических позиций материалистического понимания истории и материалистической диалектики с учетом социокультурной обусловленности этого процесса. Однако в западной философии и методологии науки XX в. фактически - особенно в годы «триумфального шествия» логического позитивизма (а у него действительно были немалые успехи) - научное знание исследовалось без учета его ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...
... И. Европоцентризм и русское национальное самосознание // Социологические исследования. 1996. № 2. С. 55–62. 24. Зиммель Г. Экскурс по проблеме: как возможно общество? // Вопросы социологии. 1993. Т. 2. № 3. С 16-26. 25. Иванов В.Н. Реформы и будущее России // Социологические исследования. 1996. № 3. С. 21-27. 26. Капусткина Е.В. Социальные реформы в России: история, современное ...
... Замечат. С.: Полемон, Герод Аттик, Аристид, Либаний. Ср. Schmid, "Der Atticismus in seinen Hauptvertretern" (1887-97). 17. Принцип детерминизма в философии. Индетерминизм. Детерминизм (от лат. determino - определяю), философское учение об объективной закономерной взаимосвязи и взаимообусловленности явлений материального и ...
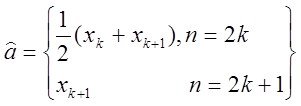



0 комментариев